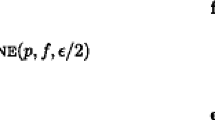An algorithm to solve the proportional network flow problem | Optimization Letters
Skip to main content
Springer Nature Link
Log in

An algorithm to solve the proportional network flow problem

  • Original Paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

Abstract

The proportional network flow problem is a generalization of the equal flow problem on a generalized network in which the flow on arcs in given sets must all be proportional. This problem appears in several natural contexts, including processing networks and manufacturing networks. This paper describes a transformation on the underlying network that reduces the problem to the equal flow problem; this transformation is used to show that algorithms that solve the equal flow problem can be directly applied to the proportional network flow problem as well, with no increase in asymptotic running time. Additionally, computational results are presented for the proportional network flow problem demonstrating equivalent performance to the same algorithm for the equal flow problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Ahuja, R.K., Magnanti, T.L., Orlin, J.B.: Network flows. Prentice Hall, New Jersey (1993)

    MATH  Google Scholar 

  2. Ahuja, R.K., Orlin, J.B., Sechi, G.M., Zuddas, P.: Algorithms for the simple equal flow problem. Manag. Sci. 45(10), 1440–1455 (1999)

    Article  MATH  Google Scholar 

  3. Ali, A.I., Kennington, J., Shetty, B.: The equal flow problem. Eur. J. Oper. Res. 36(1), 107–115 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  4. Bahçeci, U., Feyziog̃lu, O.: A network simplex based algorithm for the minimum cost proportional flow problem with disconnected subnetworks. Opt. Lett. 6(6), 1173–1184 (2012)

    Google Scholar 

  5. Calvete, H.I.: Network simplex algorithm for the general equal flow problem. Eur. J. Oper. Res. 150(3), 585–600 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  6. Chang, M.D., Chen, C.-H.J., Engquist, M.: An improved primal simplex variant for pure processing networks. ACM Trans. Math. Softw. 15(1), 64–78 (1989)

    Article  MATH  Google Scholar 

  7. Chinneck, J.W.: Processing network models of energy/environment systems. Comput. Ind. Eng. 28(1), 179–189 (1995)

    Article  Google Scholar 

  8. Chinneck, J.W., Moll, R.H.H.: Processing network models for forest management. Omega 23(5), 499–510 (1995)

    Article  Google Scholar 

  9. Clark, R., Kennington, L., Meyer, R.R., Ramamurti, M.: Generalized networks: parallel algorithms and an empirical analysis. ORSA J. Comput. 4(2), 132–145 (1992)

    Article  MATH  Google Scholar 

  10. Klingman, D., Napier, A., Stutz, J.: NETGEN: A program for generating large scale capacitated assignment, transportation and minimum cost flow networks. Manag. Sci. 20, 814–820 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  11. Koene, J.: Minimal cost flow in processing networks : a primal approach. Benders, JF (Promotor), Wessels, J (Promotor) Technical report (1982). http://alexandria.tue.nl/extra1/PRF4A/8203150.pdf

  12. Morrison, D.R., Sauppe, J.J., Jacobson, S.H.: A network simplex algorithm for the equal flow problem on a generalized network. INFORMS J. Comput. 25, 2–12 (2013)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors would like to thank one anonymous referee for comments which resulted in a significantly-improved version of this paper. All computational results were obtained with the Simulation and Optimization Laboratory at the University of Illinois, Urbana-Champaign. This research has been supported in part by the Air Force Office of Scientific Research (FA9550-10-1-0387), the Department of Defense (DoD) through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program. The third author was supported in part by (while serving at) the National Science Foundation. The views expressed in this paper are those of the authors and do not reflect the official policy or position of the United States Air Force, Department of Defense, the National Science Foundation, or the United States Government.

Author information

Authors and Affiliations

  1. Department of Computer Science, University of Illinois, Urbana-Champaign, 201 N. Goodwin Ave., Urbana, IL, 61821, USA

    David R. Morrison, Jason J. Sauppe & Sheldon H. Jacobson

Authors
  1. David R. Morrison
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jason J. Sauppe
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sheldon H. Jacobson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to David R. Morrison.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Morrison, D.R., Sauppe, J.J. & Jacobson, S.H. An algorithm to solve the proportional network flow problem. Optim Lett 8, 801–809 (2014). https://doi.org/10.1007/s11590-013-0634-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-013-0634-5

Keywords

Search

Navigation