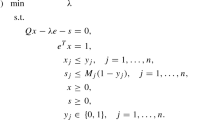Absolute value equation solution via concave minimization | Optimization Letters
Skip to main content
Springer Nature Link
Log in

Absolute value equation solution via concave minimization

  • Original Paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

The NP-hard absolute value equation (AVE) Ax − |x| = b where \(A\in R^{n\times n}\) and \(b\in R^n\) is solved by a succession of linear programs. The linear programs arise from a reformulation of the AVE as the minimization of a piecewise-linear concave function on a polyhedral set and solving the latter by successive linearization. A simple MATLAB implementation of the successive linearization algorithm solved 100 consecutively generated 1,000-dimensional random instances of the AVE with only five violated equations out of a total of 100,000 equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chung S.-J. (1989) NP-completeness of the linear complementarity problem. J. Optim. Theory Appl. 60, 393–399

    Article  MATH  MathSciNet  Google Scholar 

  2. Cottle R.W., Dantzig G. (1968) Complementary pivot theory of mathematical programming. Linear Algebra Appl. 1, 103–125

    Article  MATH  MathSciNet  Google Scholar 

  3. Cottle R.W., Pang J.-S., Stone R.E. (1992) The linear complementarity problem. Academic, New York

    MATH  Google Scholar 

  4. ILOG Incline Village, Nevada. ILOG CPLEX 9.0 User’s Manual (2003) http://www.ilog.com/products/cplex/

  5. Mangasarian O.L. (1997) Solution of general linear complementarity problems via nondifferentiable concave minimization. Acta Math. Vietnam. 22(1): 199–205 ftp://ftp.cs.wisc.edu/math-prog/tech-reports/96-10.ps

    MATH  MathSciNet  Google Scholar 

  6. Mangasarian, O.L Absolute value programming. Technical Report 05-04, Data Mining Institute, Computer Sciences Department, University of Wisconsin, Madison, Wisconsin, September (2005) ftp://ftp.cs.wisc.edu/pub/dmi/tech-reports/05-04.ps. Comput. Optim. Appli. (to appear)

  7. Mangasarian, O.L., Meyer, R.R. Absolute value equations. Technical Report 05–06, Data Mining Institute, Computer Sciences Department, University of Wisconsin, Madison, Wisconsin, December 2005. Linear Algebra and Its Applications (to appear) ftp://ftp.cs.wisc.edu/pub/dmi/tech-reports/05-06.ps

  8. MATLAB: User’s guide. The MathWorks, Inc., Natick, MA 01760 (1994–2001) http://www.mathworks.com

  9. Polyak B.T. (1987) Introduction to optimization. Optimization Software, Inc., Publications Division, New York

    MATH  Google Scholar 

  10. Rockafellar R.T. (1970) Convex Analysis. Princeton University Press, Princeton

    MATH  Google Scholar 

  11. Rohn J. (2004) A theorem of the alternatives for the equation A x + B|x| = b. Linear Multilinear Algebra 52(6): 421–426 http://www.cs.cas.cz/rohn/publist/alternatives.pdf

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computer Sciences Department, University of Wisconsin, Madison, WI, 53706, USA

    O. L. Mangasarian

  2. Department of Mathematics, University of California at San Diego, La Jolla, CA, 92093, USA

    O. L. Mangasarian

Authors
  1. O. L. Mangasarian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. L. Mangasarian.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mangasarian, O.L. Absolute value equation solution via concave minimization. Optimization Letters 1, 3–8 (2007). https://doi.org/10.1007/s11590-006-0005-6

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-006-0005-6

Keywords

Search

Navigation