A statistical shape modeling approach for predicting subject-specific human skull from head surface | Medical & Biological Engineering & Computing Skip to main content
Springer Nature Link
Log in

A statistical shape modeling approach for predicting subject-specific human skull from head surface

  • Original Article
  • Published:
Medical & Biological Engineering & Computing Aims and scope Submit manuscript

Abstract

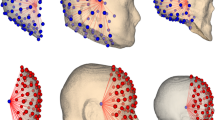
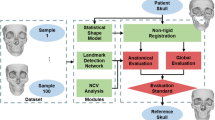
Human skull is an important body structure for jaw movement and facial mimic simulations. Surface head can be reconstructed using 3D scanners in a straightforward way. However, internal skull is challenging to be generated when only external information is available. Very few studies in the literature focused on the skull generation from outside head information, especially in a subject-specific manner with a complete skull. Consequently, this present study proposes a novel process for predicting a subject-specific skull with full details from a given head surface using a statistical shape modeling approach. Partial least squared regression (PLSR)–based method was used. A CT image database of 209 subjects (genders—160 males and 49 females; ages—34–88 years) was used for learning head-to-skull relationship. Heads and skulls were reconstructed from CT images to extract head/skull feature points, head/skull feature distances, head–skull thickness, and head/skull volume descriptors for the learning process. A hyperparameter turning process was performed to determine the optimal numbers of head/skull feature points, PLSR components, deformation control points, and appropriate learning strategies for our learning problem. Two learning strategies (point-to-thickness with/without volume descriptor and distance-to-thickness with/without volume descriptor) were proposed. Moreover, a 10-fold cross-validation procedure was conducted to evaluate the accuracy of the proposed learning strategies. Finally, the best and worst reconstructed skulls were analyzed based on the best learning strategy with its optimal parameters. The optimal number of head/skull feature points and deformation control points are 2300 and 1300 points, respectively. The optimal number of PLSR components ranges from 4 to 8 for all learning configurations. Cross-validation showed that grand means and standard deviations of the point-to-thickness, point-to-thickness with volumes, distance-to-thickness, and distance-to-thickness with volumes learning configurations are 2.48 ± 0.27 mm, 2.46 ± 0.19 mm, 2.46 ± 0.15 mm, and 2.48 ± 0.22 mm, respectively. Thus, the distance-to-thickness is the best learning configuration for our head-to-skull prediction problem. Moreover, the mean Hausdorff distances are 2.09 ± 0.15 mm and 2.64 ± 0.26 mm for the best and worst predicted skull, respectively. A novel head-to-skull prediction process based on the PLSR method was developed and evaluated. This process allows, for the first time, predicting 3D subject-specific human skulls from head surface information with a very good accuracy level. As perspective, the proposed head-to-skull prediction process will be integrated into our real-time computer-aided vision system for facial animation and rehabilitation.

Graphical abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Y. Lee, D. Terzopoulos, K. Waters (1993), Constructing physics-based facial models of individuals, Proc. of Graphics Interface ’93 Conf. 1–8. https://doi.org/10.20380/GI1993.01

  2. K. Kähler, J. Haber, H.-P. Seidel (2001), Geometry-based muscle modeling for facial animation. In: Graph. Interface, pp. 37–46. doi:https://doi.org/10.20380/GI2001.05

  3. Claes P, Vandermeulen D, De Greef S, Willems G, Clement JG, Suetens P (2010) Computerized craniofacial reconstruction: conceptual framework and review. Forensic Sci Int 201:138–145. https://doi.org/10.1016/j.forsciint.2010.03.008

    Article  PubMed  Google Scholar 

  4. Wei M, Liu Y, Dong H, El Saddik A (2017) Human head stiffness rendering. IEEE Trans Instrum Meas 66:2083–2096. https://doi.org/10.1109/TIM.2017.2676258

    Article  Google Scholar 

  5. Ping HY, Abdullah LN, Sulaiman PS, Halin AA (2013) Computer facial animation: a review. Int J Comput Theory Eng 5:658–662. https://doi.org/10.7763/ijcte.2013.v5.770

    Article  Google Scholar 

  6. K. Waters, D. Terzopoulos (1990), A physical model of facial tissue and muscle articulation, in: [1990] Proc. First Conf. Vis. Biomed. Comput., 1990: pp. 77–82. doi:https://doi.org/10.1109/VBC.1990.109305

  7. Wang SF, Lai SH (2011) Reconstructing 3D face model with associated expression deformation from a single face image via constructing a low-dimensional expression deformation manifold. IEEE Trans Pattern Anal Mach Intell 33:2115–2121. https://doi.org/10.1109/TPAMI.2011.88

    Article  PubMed  Google Scholar 

  8. Marcos S, Gómez-García-Bermejo J, Zalama E (2010) A realistic, virtual head for human–computer interaction. Interact Comput 22:176–192. https://doi.org/10.1016/j.intcom.2009.12.002

    Article  Google Scholar 

  9. Matsuoka A, Yoshioka F, Ozawa S, Takebe J (2019) Development of three-dimensional facial expression models using morphing methods for fabricating facial prostheses. J Prosthodont Res 63:66–72. https://doi.org/10.1016/j.jpor.2018.08.003

    Article  PubMed  Google Scholar 

  10. Turban L, Girard D, Kose N, Dugelay JL (2015) From Kinect video to realistic and animatable MPEG-4 face model: a complete framework, 2015 IEEE Int. Conf Multimed Expo Work ICMEW 2015:1–6. https://doi.org/10.1109/ICMEW.2015.7169783

    Article  Google Scholar 

  11. Nielsen JD, Madsen KH, Puonti O, Siebner HR, Bauer C, Madsen CG, Saturnino GB, Thielscher A (2018) Automatic skull segmentation from MR images for realistic volume conductor models of the head: assessment of the state-of-the-art. Neuroimage. 174:587–598. https://doi.org/10.1016/j.neuroimage.2018.03.001

    Article  PubMed  Google Scholar 

  12. Minnema J, van Eijnatten M, Kouw W, Diblen F, Mendrik A, Wolff J (2018) CT image segmentation of bone for medical additive manufacturing using a convolutional neural network. Comput Biol Med 103:130–139. https://doi.org/10.1016/j.compbiomed.2018.10.012

    Article  PubMed  Google Scholar 

  13. Claes P, Vandermeulen D, Suetens R, Willems G, De Greef S (2008) Volumetric deformable face models for cranio-facial reconstruction, ISPA 2005. Proc. 4th Int. Symp. Image Signal Process. Anal 2005:353–358. https://doi.org/10.1109/ispa.2005.195437

    Article  Google Scholar 

  14. R. Liang, Y. Lin, L. Jiang, J. Bao, X. Huang (2009), Craniofacial model reconstruction from skull data based on feature points, Proc. - 2009 11th IEEE Int. Conf. Comput. Des. Comput. Graph. CAD/Graphics 2009. 602–605. doi:https://doi.org/10.1109/CADCG.2009.5246828

  15. Yuru Pei, Hongbin Zha, Zhongbiao Yuan (2008), Facial feature estimation from the local structural diversity of skulls. In: 2008 19th Int. Conf. Pattern Recognit., IEEE, 2008: pp. 1–4. doi:https://doi.org/10.1109/ICPR.2008.4761858

  16. Y.F. Zhang, M.Q. Zhou, G.H. Geng, J. Feng (2010), Face appearance reconstruction based on a regional statistical craniofacial model (RCSM). Proc. - Int. Conf. Pattern Recognit. 1670–1673. doi:https://doi.org/10.1109/ICPR.2010.413

  17. Shui W, Zhou M, Deng Q, Wu Z, Duan F (2010) 3D craniofacial reconstruction using reference skull–face database. Int Conf Image Vis Comput New Zeal:1–7. https://doi.org/10.1109/IVCNZ.2010.6148864

  18. Yang Y, Zhou M, Lu K, Duan F, Li Y, Tian Y, Wu Z (2014) Skull identification via correlation measure between skull and face shape. IEEE Trans Inf Forensics Secur 9:1322–1332. https://doi.org/10.1109/tifs.2014.2332981

    Article  Google Scholar 

  19. Duan F, Huang D, Tian Y, Lu K, Wu Z, Zhou M (2015) 3D face reconstruction from skull by regression modeling in shape parameter spaces. Neurocomputing. 151:674–682. https://doi.org/10.1016/j.neucom.2014.04.089

    Article  Google Scholar 

  20. F. Bai, C. Zhengxin, X. Qiao, D. Qingqiong, F. Duan, Y. Tian (2017), Face reconstruction from skull based on Least Squares Canonical Dependency Analysis, 2016 IEEE Int. Conf. Syst. Man, Cybern. SMC 2016 - Conf. Proc. 3612–3617. doi:https://doi.org/10.1109/SMC.2016.7844794

  21. D. Madsen, M. Lüthi, A. Schneider, T. Vetter (2018), Probabilistic joint face-skull modelling for facial reconstruction. In: Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2018: pp. 5295–5303

  22. Pearson K LIII On lines and planes of closest fit to systems of points in space. London, Edinburgh, Dublin Philos. Mag. J. Sci 2(1901):559–572

  23. Hotelling H (1933) Analysis of a complex of statistical variables into principal components. J Educ Psychol 24:417

    Article  Google Scholar 

  24. Soummer R, Pueyo L, Larkin J (2012) Detection and characterization of exoplanets and disks using projections on Karhunen–Loève eigenimages. Astrophys J Lett 755:L28

    Article  Google Scholar 

  25. Wold S, Geladi P, Esbensen K, Öhman J (1987) Multi-way principal components- and PLS-analysis. J Chemom 1:41–56

    Article  CAS  Google Scholar 

  26. Garthwaite PH (1994) An interpretation of partial least squares. J Am Stat Assoc 89:122–127

    Article  Google Scholar 

  27. Lee DD, Seung HS (1999) Learning the parts of objects by non-negative matrix factorization. Nature. 401:788–791

    Article  CAS  Google Scholar 

  28. Paatero P, Tapper U (1994) Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values. Environmetrics. 5:111–126

    Article  Google Scholar 

  29. Ju T, Schaefer S, Warren J (2005) Mean value coordinates for closed triangular meshes. In: ACM SIGGRAPH 2005 Pap. - SIGGRAPH ‘05. In: ACM press. New York, USA, New York, p 561. https://doi.org/10.1145/1186822.1073229

    Chapter  Google Scholar 

  30. Clark K, Vendt B, Smith K, Freymann J, Kirby J, Koppel P, Moore S, Phillips S, Maffitt D, Pringle M, Tarbox L, Prior F (2013) The Cancer Imaging Archive (TCIA): maintaining and operating a public information repository. J. Digit. Imaging 26:1045–1057. https://doi.org/10.1007/s10278-013-9622-7

    Article  PubMed  PubMed Central  Google Scholar 

  31. Vallières M, Kay-Rivest E, Perrin LJ, Liem X, Furstoss C, Aerts HJWL, Khaouam N, Nguyen-Tan PF, Wang C-S, Sultanem K, Seuntjens J, El Naqa I (2017) Radiomics strategies for risk assessment of tumour failure in head-and-neck cancer. Sci Rep 7:10117. https://doi.org/10.1038/s41598-017-10371-5

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  32. Pieper S, Halle M, Kikinis R (2005) 3D Slicer, pp 632–635. https://doi.org/10.1109/isbi.2004.1398617

    Book  Google Scholar 

  33. Dao TT, Pouletaut P, Charleux F, Lazáry Á, Eltes P, Varga PP, Ho Ba Tho MC (2015) Multimodal medical imaging (CT and dynamic MRI) data and computer-graphics multi-physical model for the estimation of patient specific lumbar spine muscle forces. Data Knowl. Eng 96–97:3–18. https://doi.org/10.1016/j.datak.2015.04.001

  34. Lorensen WE, Cline HE (1987) Marching cubes: a high resolution 3D surface construction algorithm. ACM SIGGRAPH Comput Graph 21:163–169. https://doi.org/10.1145/37402.37422

    Article  Google Scholar 

  35. Field DA (1988) Laplacian smoothing and Delaunay triangulations. Commun Appl Numer Methods 4:709–712. https://doi.org/10.1002/cnm.1630040603

    Article  Google Scholar 

  36. Smith KE, Bhatia G, Vannier MW (1995) Assessment of mass properties of human head using various three-dimensional imaging modalities. Med Biol Eng Comput 33:278–284. https://doi.org/10.1007/BF02510500

    Article  CAS  PubMed  Google Scholar 

  37. Bernardini F, Mittleman J, Rushmeier H, Silva C, Taubin G (1999) The ball-pivoting algorithm for surface reconstruction. IEEE Trans Vis Comput Graph 5:349–359. https://doi.org/10.1109/2945.817351

    Article  Google Scholar 

  38. Fabri A, Giezeman G-J, Kettner L, Schirra S, Schnherr S (2000) On the design of CGAL a computational geometry algorithms library. Softw Pract Exp 30:1167–1202. https://doi.org/10.1002/1097-024X(200009)30:11<1167::AID-SPE337>3.0.CO;2-B

    Article  Google Scholar 

  39. Marden S, Guivant J (2012) Improving the performance of ICP for real-time applications using an approximate nearest neighbour search. Australas Conf Robot Autom ACRA:3–5

  40. Besl PJ, McKay ND (1992) A method for registration of 3-D shapes. In: Schenker PS (ed) Sens. Fusion IV Control Paradig. Data Struct, pp 586–606. https://doi.org/10.1117/12.57955

    Chapter  Google Scholar 

  41. P. Alliez, É.C. De Verdière, O. Devillers, M. Isenburg (2003), Isotropic surface remeshing, Proc. - SMI 2003 Shape Model. Int. 2003. 2003 (2003) 49–58. doi:https://doi.org/10.1109/SMI.2003.1199601

  42. R.B. Rusu, S. Cousins (2011), 3D is here: Point Cloud Library (PCL), in: 2011 IEEE Int. Conf. Robot. Autom., IEEE, 2011: pp. 1–4. doi:https://doi.org/10.1109/ICRA.2011.5980567

  43. Geladi P, Bruce R (1986) Kowalski, partial least-squares regression: a tutorial. J Optoelectron Adv Mater 10:1–17. https://doi.org/10.1016/0003-2670(86)80028-9

    Article  Google Scholar 

  44. Lindgren F, Geladi P, Wold S (1993) The kernel algorithm for PLS. J Chemom 7:45–59. https://doi.org/10.1002/cem.1180070104

    Article  CAS  Google Scholar 

  45. Dayal BS, Macgregor JF (1997) Improved PLS algorithms. J Chemom 11:73–85. https://doi.org/10.1002/(SICI)1099-128X(199701)11:1<73::AID-CEM435>3.0.CO;2-%23

    Article  CAS  Google Scholar 

  46. Free 3D Models, (n.d.). www.free3d.com

  47. Myronenko A, Song X (2010) Point set registration: coherent point drifts. IEEE Trans Pattern Anal Mach Intell 32:2262–2275. https://doi.org/10.1109/TPAMI.2010.46

    Article  PubMed  Google Scholar 

  48. Floater MS (2003) Mean value coordinates. Comput Aided Geom Des 20:19–27. https://doi.org/10.1016/S0167-8396(03)00002-5

    Article  Google Scholar 

  49. N. Aspert, D. Santa-Cruz, T. Ebrahimi (1978), MESH: measuring errors between surfaces using the Hausdorff distance. In: proceedings IEEE Int. Conf. Multimed. Expo, IEEE,: pp. 705–708. doi:https://doi.org/10.1109/ICME.2002.1035879

  50. Pandzic IS, Forchheimer R (2003) MPEG-4 facial animation. https://doi.org/10.1002/ima.10072

    Book  Google Scholar 

  51. Prendergast PM (2012) Facial anatomy. Adv Surg Facial Rejuvenation Art Clin Pract 9783642178:3–14. https://doi.org/10.1007/978-3-642-17838-2_1

    Article  Google Scholar 

  52. Sederberg TW, Parry SR (1986) Free-form deformation of solid geometric models. ACM SIGGRAPH Comput. Graph. 20:151–160

    Article  Google Scholar 

  53. Nguyen TN, Dakpe S, Ho Ba Tho MC, Dao TT (2020) Real-time computer vision system for tracking simultaneously subject-specific rigid head and non-rigid facial mimic movements using a contactless sensor and system of systems approach. Comput. Methods Programs Biomed:105410. https://doi.org/10.1016/j.cmpb.2020.105410

  54. Godoy JL, Vega JR, Marchetti JL (2014) Relationships between PCA and PLS-regression. Chemom Intell Lab Syst 130:182–191. https://doi.org/10.1016/j.chemolab.2013.11.008

    Article  CAS  Google Scholar 

  55. Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G (2008) The graph neural network model. IEEE Trans Neural Netw 20:61–80

    Article  Google Scholar 

  56. R. Bhalodia, S.Y. Elhabian, L. Kavan, R.T. Whitaker, Deepssm: a deep learning framework for statistical shape modeling from raw images. In: Int. Work. Shape Med. Imaging, 2018: pp. 244–257

  57. M. Reuter, C. Wachinger, H. Lombaert, B. Paniagua, M. Lüthi, B. (2018) Egger. Shape in medical imaging: international workshop, ShapeMI 2018, held in conjunction with MICCAI 2018, Granada, Spain, September 20, 2018, Proceedings, Springer, 2018

  58. Bronstein MM, Bruna J, LeCun Y, Szlam A, Vandergheynst P (2017) Geometric deep learning: going beyond Euclidean data. IEEE Signal Process Mag 34:18–42

    Article  Google Scholar 

  59. Dao TT, Pouletaut P, Lazáry Á, Ho Ba Tho MC (2017) Multimodal medical imaging fusion for patient specific musculoskeletal modeling of the lumbar spine system in functional posture. J Med Biol Eng 37:739–749

Download references

Acknowledgments

This work was carried out and funded in the framework of the Labex MS2T. It was supported by the French Government, through the program “Investments for the future” managed by the National Agency for Research (Reference ANR-11-IDEX-0004-02). We also acknowledge the “Hauts-de-France” region for funding.

Author information

Authors and Affiliations

  1. Université de technologie de Compiègne, CNRS, UMR 7338 Biomechanics and Bioengineering, Centre de recherche Royallieu, 60 319, Compiègne, CS, France

    Tan-Nhu Nguyen & Tien-Tuan Dao

  2. Ho Chi Minh City University of Technology and Education, Ho Chi Minh City, Vietnam

    Vi-Do Tran

  3. Thu Dau Mot University, Binh Duong, Vietnam

    Ho-Quang Nguyen

Authors
  1. Tan-Nhu Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vi-Do Tran
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ho-Quang Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Tien-Tuan Dao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tien-Tuan Dao.

Ethics declarations

Conflict of interest

The authors declare that they have no conflicts of interest.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, TN., Tran, VD., Nguyen, HQ. et al. A statistical shape modeling approach for predicting subject-specific human skull from head surface. Med Biol Eng Comput 58, 2355–2373 (2020). https://doi.org/10.1007/s11517-020-02219-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11517-020-02219-4

Keywords

Search

Navigation