1 Introduction

The number of electronic devices working in the same spatial space was small in the past. Furthermore, researchers in this field did not have to care about the degradation of the environment and the electromagnetic interference (EMI) between these appliances [1]. With the massive growth of electronic devices in terms of compact size and built-in integrated radio frequency (RF) circuits, holding the electronic devices together in the same spatial space results in electromagnetic interference. This interference prevents the compatibility of these devices from working together efficiently. Usually, the degradation in the system performance resulting from the EMI is lately detected, and replacing the defected parts requires a high cost. Therefore, the immunity of the new products is preferred to be performed in the electromagnetic compatibility (EMC) laboratory against radiation before releasing them to the markets. The EU EMC Directive adopted Laws in 1992 to oblige all electronic devices or appliance manufacturers to submit their products to the electromagnetic compatibility test before releasing them into the markets [2]. One of the mandatory parts of this test is the electromagnetic sensors, i.e., the reference antenna. The antennas used for the EMC test in the far-field measurement should have specific characteristics such as wide bandwidth, low fluctuations in the gain, consistent radiation pattern, steady phase center, and good antenna factor (AF) [3].

The frequency band from 0.7 GHz to 2.4 GHz is occupied by some critical applications like GSM, GPS, and LTE. Recently, the band (2.5 GHz up to 6 GHz) has been utilized for covering some wireless applications like Wi-fi, WiMAX, WLAN, PAN, and 5G mid-band [4]. By doing so, one of the motivations here is to design an antenna that can cover the whole frequency band from 0.7 GHz up to 6.5 GHz. Where these bands might be of interest, to protect wireless communication from EMI.

Several means were employed to estimate the strength of the electrical field emitted from the DUT. For instance, the reverberation chamber (RC), the open site method (OATS), the semi-anechoic chamber (SAC), and the full-anechoic chamber (FAC). This work will focus on the reference antennae that are used in EMC chamber, which utılizes the last two methods, SAC and FAC [5]. Many antenna types have served as reference antennas inside the EMC (SAC or FAR) chamber in the bands 30–1000 MHz and 1000–6000 MHz including VHF and UHF bands. The VHF and UHF bands are classified based on the European Telecommunications Standards Institute (ETSI). The VHF band is covered by a biconical or log periodic antenna, while the Horn antenna covers the UHF band above 1 GHz [6].

The classical antennas are large in size and heavy in weight. Therefore, using printed circuit board technology (PCB) to design compact structures has a lot of advantages like low cost, low profile, and ease to fabricate [7]. On the other hand, microstrip antennas suffer from narrow bandwidth and low efficiency, which are considered significant issues in EMC applications. This makes the using of the monopole and dipole printed antennas as a basic element for the proposed structures is the best way to overcome these issues.

Several printed broadband antennas have been proposed in the last decade. Ultra-Wideband printed Vivaldi antenna was presented in [8], where the length of the structure has been reduced using a transition from strip line to slot line that reflects stability in gain and radiation pattern transition. Authors in [9] discussed the effect of three major designing parameters on Microstrip fed Vivaldi antenna with the help of parametric sweep features of CST Microwave Studio. Consequently, the results showed that both resonant frequency and radiation efficiency are controlled directly by changing the flare length and slot width. Furthermore, the optimized structure was built on FR-4 substrate and presented wide impedance bandwidth from 0.8 GHz to 1.8 GHz.

The concept of Chebyshev transformer was applied to design tapered slot antenna in Ref [10]. The realized Vivaldi antenna operated from 0.4 up to 3 GHz and based on Duroid substate of 297 × 190 mm2 size. Moreover, maximum realized gain of 11.6 dBi at 2 GHz and 1.23 GHz impedance bandwidth were achieved. An improved structure of UWB Vivaldi antenna operating from 0.8 up to 3.8 GHz was proposed in [11]. SMD resistive was loaded at the bottom of the exponential part of antenna to enhance the VSWR. Adding this resistor reflected a maximum gain of 8.1 dBi at 3.8 GHz with relativity smal1 size of 150 × 150 mm2. Authors in [12] proposed a novel tapered slot edge with resonant cavity (TSERC) structure to extend the low-end bandwidth limit of the proposed structure (start from 0.5 GHz) compared to the printed conventional Vivaldi antenna (start from 1.2 GHz). By doing so, 19.5% size reduction with relative bandwidth of 14.6% were achieved in addition to the maximum gain of 8.1 dBi at 2 GHz.

In [13], the authors proposed a compact broadband log-periodic dipole array antenna operating from 0.55 GHz to 9 GHz with a maximum gain of 7.8 dBi using 49 dipole elements. Size reduction of 27% and 20% was achieved by loading a hat shape for the first three elements and the T-shape for the next three, while meandered line and trapezoidal tapered techniques were utilized to get a wide bandwidth. Another log-periodic dipole array antenna working from 0.5 GHz to 10 GHz was presented in [14]. Both size reduction and bandwidth enhancement were obtained by replacing the classical dipoles with dual-band dipoles with wider bandwidth achieving a maximum realized gain of 6 dBi. Furthermore, a 40% size reduction has been achieved by utilizing 25 dual-band dipole elements instead of 40 for the conventional design. A wideband 0.4 GHz to 8 GHz printed log-periodic dipole array antenna was proposed in [15] for low-frequency applications. The extended bandwidth has been achieved by changing the shape of the most extended dipole to a triangular shape and optimizing the next four dipoles. However, the return losses do not satisfy the VSWR < 2 for the whole frequency band.

A pair of printed broadband Vivaldi antennas with a coaxial feeding method operating from 0.5 GHz to 4 GHz was designed, fabricated, and tested [16]. Moreover, the proposed design serves as a reference antenna for EMC measurement since it exhibits stable radiation characteristics and a maximum gain of 6.2 dBi. In [17], a small size wideband printed Vivaldi antenna operating from 1 GHz to 20 GHz was presented. Meanwhile, the authors used a high chip resistor and short pin to enhance the impedance bandwidth compared to the conventional structure with a 50% size reduction.

The printed Vivaldi antenna has been widely used in various wireless applications. However, its effectiveness for EMC measurements inside the EMC chamber has not been previously reported. The traditional antenna has two major drawbacks, large weight and big size. The weight is a challenge when moving or replacing the antenna while testing. Moreover, the large size may cause configuration issues during testing, especially when the antenna is vertically oriented with the presence of interference with the ground plane of the EMC chamber impacting the accuracy of the measurement results.

At the higher frequencies (1 GHz and beyond), the Horn antenna is preferred to serve as a reference antenna for EMI measurements. This antenna provides high directivity and gain, which makes it helpful at high frequencies since the attenuation is greater and the dynamic range is more critical [18]. To overcome the weight and size limitations of the Horn antenna, a printed broadband high gain Vivaldi printed antenna has been designed and fabricated in this work to serve as a reference antenna for EMC measurements. The proposed structure has a bandwidth of 4.7 GHz, which covers most interference emitted from the DUT in the band from 0.8 GHz up to 5.5 GHz. The novelty of the presented design lies in the significant reduction of the antenna’s size and weight. The reduction of the presented design’s dimensions in length and width compared to the commercial ones (PowerLOG® PRO 30800 and TBMA4) are (64% & 67%) and (25% & 22%), respectively. In terms of weight reduction, the proposed design has a weight of 70 g only compared to 8.8 kg and 15 kg for the PowerLOG® PRO 30,800 and TBMA4 antennas, respectively. Meantime, these achievements came along with fulfilling all other EMC test requirements such as the wide bandwidth of 4.7 GHz, wide beamwidth, improved gain of 10.7 dB, and maintained antenna factor. Moreover, this paper is organized as follows: Sect. 2 describes the basic concepts of the Vivaldi antenna design, while feeding method are presented in Sect. 3. Section 4 shows the simulation and measurement results, and finally, Sect. 5 demonstrates a brief conclusion.

2 Conventional Vivaldi Antenna

This antenna is called a traveling wave antenna because its tapered slot acts as a transmission line or waveguide to transfer the electromagnetic waves from the fed line to the free space. The radiation mechanism is smoothy, and the continuous transition is similar to the Horn antenna. Therefore, it is sometimes called a 2-D Horn antenna [16]. The slot antenna has different kinds, like linearly tapered slot antennas, constant width slot antennas, and exponentially tapered slot antennas (Vivaldi) [19]. Some parameters in this design have their own conditions that should be satisfied. For instance, antenna length (Lsub) should be longer than the lower frequency wavelength, which directly impacts the bandwidth. In contrast, antenna width (Wsub) should be longer than half the wavelength of the lower frequency and decreasing the width (Wsub) will increase the bandwidth. It is worth mentioning that an increase in the width of aperture mouth of the Vivaldi antenna (WMax) decreases the lower frequency and thus provides wider bandwidth. Moreover, the bandwidth can also be improved with increasing the taper length (LT) which should be one order of wavelength of the lower frequency [20]. The Vivaldi antenna is based on an exponentially tapered slot, which can be described using the equation reported in [21].

$$\:x={C}_{1}{e}^{ry}+{C}_{2}$$
(1)

The coefficients C1 and C2 are calculated using the coordinate of the starting and the end points of the exponential curve.

$$\:{C}_{1}=\frac{{x}_{2}-{x}_{1}}{{e}^{{ry}_{2}}-{e}^{{ry}_{1}}}\:,$$
$$\:{C}_{2}=\frac{{x}_{1}{e}^{{ry}_{2}}-{x}_{1}{e}^{{ry}_{1}}}{{e}^{{ry}_{2}}-{e}^{{ry}_{1}}}\:,$$

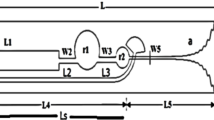
where r is the tapered rate of 0.0316, \(\:({x}_{1}\), \(\:{y}_{1})\:and\:\)(\(\:{x}_{2}\), \(\:{y}_{2})\) denote the slot-lines start and end points pairs. The geometrical shape of this antenna is shown in Fig. 1, while the optimum parameters are listed in Table 1.

Table 1 The optimum antenna parameters in mm
Full size table
Fig. 1
figure 1

The geometrical shape of the antenna: (a) front view and (b) back view

Full size image

2.1 Feeding Method

The microstrip feed line width \(\:{w}_{f}\) for any impedance \(\:{z}_{0}\) can approximaltely be calculated from the following equation in [7].

$$\:{z}_{0}=\frac{87}{\sqrt{{\epsilon\:}_{reff}+1.41}}\text{ln}(\frac{5.98\times\:h}{0.8\times\:{w}_{f}})$$
(2)

For characteristic impedance \(\:{z}_{0}=50\:{\Omega\:}\), h = 1.6 mm and \(\:{\epsilon\:}_{reff}=4.2\) for FR-4 substrate, the microstrip line width is \(\:{w}_{f}\:\)= 3.03 mm, and this part is balanced since it will connect to the 50 Ω coaxial cable.

where, the effective relative permittivity is calculated based on the reported equation in [7].

$$\:{\epsilon\:}_{eff}=\frac{{\epsilon\:}_{r}+1}{2}+\frac{{\epsilon\:}_{r}+1}{2}{[1+12\frac{h}{w}]}^{-\frac{1}{2}}$$
(3)

Using the same equation, the characteristic impedance of the microstrip line connected to the unbalance part (antenna) is 90 \(\:{\Omega\:}\) at 1 mm width. Moreover, to match the two impedances (90 Ω and 50 Ω), a tapered line has been introduced to have a smooth transition and offer wide bandwidth [2]. The electromagnetic coupling feeding has been employed, which is based on the microstrip quarter-wavelength line/slot line transition power [22]. Suppose we have an input wave of \(\:\text{sin}wt\) as shown in Fig. 2a, the electromagnetic wave travels along the strip line and reverse its direction at the edge. The reflected signal will have a phase shift of 2π or zero at the center point as presented in [21] and as a result the phase shift will equal to 2π or zero at the center point presented in Fig. 2b.

Fig. 2
figure 2

The basic idea of electromagnetic coupling with a quarter wavelength of strip- line/slot

Full size image

The wideband behavior of impedance matching has been achieved by adopting stubs in microstrip and slot lines. These stubs have different shapes like radial stub and cavity slot, as shown in Fig. 3. The radial stub is an open-circuit stub that is used as an alternative for the straight quarter wavelength microstrip line for two reasons. Firstly, the radial stub offers a wideband short circuit wider than the linear quarter wavelength microstrip line. Secondly, at the low frequencies, the quarter wavelength microstrip line is significantly long and might not be very practical to implement with a straight quarter wavelength microstrip line.

Fig. 3
figure 3

The electromagnetic coupling feeding method with radial stub

Full size image

To provide deep insight on the effect of radial stub in matching the proposed Vivaldi antenna with 50 Ω input port, two influencing factors (the radius R and angle ‘theta’ θ) are swept, optimized and analysis to study the effects of their variations on the impedance matching of the antenna. Figure 4 (a) presents the reflection coefficient versus frequency for different values of radial stub radius R. decreasing the length of the radial stub will increase the operational bandwidth up to 3 GHz at R = 9 mm. The next step is to change the radial stub angle θ with fixed value of R = 9 mm as shown in Fig. 4 (b). Increasing the value of θ will enhance the reflection coefficient at the lower frequency band at 1 GHz on the price of reduce the whole operational frequency range. The selected value of θ = 25⁰ is the optimum since it enhances the reflection coefficient at the lower frequency band and maintains on the same operational frequency range. The optimized values of electromagnetic coupling technique parameters are listed in Table 2.

Fig. 4
figure 4

The reflection coefficient versus frequency for: (a) changing R values (9 mm up to 18 mm) and (b) changing theta value (from 15⁰ up to 55⁰)

Full size image
Table 2 The optimum feeding parameters in mm
Full size table

This antenna has been designed and modeled in the CST Microwave Studio package based on the Finite Integration Technique (FIT) [23]. Figure 5(a) presents the simulated reflection coefficient versus frequency, while the simulated realized gain is shown in Fig. 5(b).

Fig. 5
figure 5

The simulated results of the conventional Vivaldi antenna: (a) reflection coefficient and (b) realized gain

Full size image

It can be seen that the reflection coefficient of the conventional design offers an acceptable bandwidth (0.85–5 GHz). On the other hand, the non-smoothy gain with low values through the whole band (in particular at the lower bands) would reflect an antenna factor with a very small margin for the compliance test. In fact, the antenna factor is one of the critical parameters to decide whether this antenna is good to use as a reference antenna in EMC measurement applications or not.

3 Modified Vivaldi Antenna

The gain measures how much the antenna gained from the electromagnetic waves in one direction compared to the omnidirectional radiation. However, the antenna factor is an essential metric to measure the possibility of using this antenna as a reference for EMC measurements. It can be considered as a transfer function representing the division of the captured electrical field by the induced voltage across the antenna terminals. According to the considerations of EMI antenna design, the traditional value of the antenna factor is different from one antenna to another. It can be evaluated easily from the antenna gain in dBi using (4) since the realized gain is another image to the antenna factor [16].

$$\:AF=20\text{log}\left[\frac{2\pi\:}{\lambda\:}\:\sqrt{\frac{2.4}{{10}^{\left(G\right(dBi)/10)}}}\right]$$
(4)

The antenna factor is utilized to compute the electrical field strength (\(\:{E}_{Max}\)) of the device under test with the help of (5) to compare it with the standard limits in class A and class B. Therefore, a flat antenna factor with frequency will provide enough margin for the test regarding the upper limits in these standards. The high margin value will make the test more immune and robust against measurement noise, especially at high frequencies which represents our goal.

$$\:{E}_{Max}=AF+{V}_{r}$$
(5)

Enhancing the antenna factor to accommodate the intended purpose directly depends on the antenna gain in dBi as in (4). The improvement and smooth transition of antenna gain depends on the basic structure of the antenna. For instance, introducing slots on the patch antenna might have led to improving the impedance matching [24], getting additional resonance frequencies [25], and improving the gain [26]. This work introduced two types of slots: rectangular slots and a pair of reversed triangular slots. Furthermore, the parametric sweep operation has been performed on the dimensions of these slots as follows.

3.1 Rectangular Slots

Two rectangular slots were engraved on both sides of the antenna close to the feeding point, which reflects better performance in reshaping the gain and making the transition smooth, as shown in Fig. 6. The optimum result of the realized gain is at slots length Ls1 = 55 mm, in which the antenna gain has a flatter response than other gain curves. For instance, when Ls1 = 70 mm, the deployed slot would be too close to the feeding point, and the realized gain decreases at the lower band at 2 GHz due to the electromagnetic coupling between the engraved rectangular slots and the feeding point.

Fig. 6
figure 6

The realized gain versus frequency for different values of slots length Ls1

Full size image

Figure 7 demonstrates the optimum simulated realized gain and corresponding antenna factor versus frequency at slots length Ls1 = 55 mm. By observing the antenna factor results in Fig. 7(b), it has been found that the realized gain needs more enhancement to achieve an acceptable level of the antenna factor compared to the classical antenna. Therefore, another method is planned to be utilized to maximize the field and gain at the higher frequency bands in the next section.

Fig. 7
figure 7

The simulated results of, (a) the realized gain in dBi versus frequency, and (b) the antenna factor in dBm− 1

Full size image

3.2 Reversed Triangle Slots

The key to enhancing the antenna factor is manipulating the realized gain since they have a direct connection as in Eq. (4). Recently, several techniques have been proposed to enhance the antenna gain to suit many applications, like metamaterials [27, 28], reflectors [29, 30], superstrate [31, 32], and slots [26]. In particular, the realized gain of the Vivaldi antenna has also been enhanced with different techniques, like inserting a load resistor at the end of the coupling gap [33], using ultrathin microwave absorbing material at the edges of the antenna [34], and utilizing an index near zero meta-surface in the aperture [35]. In this work, two reversed triangular slots were added to the antenna’s top part, as shown in Fig. 8.

Fig. 8
figure 8

The geometrical shape of the final structure after adding triangular slots where \(\:{W}_{ts}\) = 48.55 mm and \(\:{L}_{ts}\)= 59 mm

Full size image

The position and the dimensions of the slots have been adjusted with the help of surface current distribution. Figure 9 presents the tangent component of the electrical field distribution with and without using two triangular slots. It is clear that the radiation at the side of the antenna is significantly reduced when engraving the two slots, so the radiation gets more directive in this case.

Fig. 9
figure 9

The tangent component of the electrical field distribution (a) without slots and (b) with slots

Full size image

The triangular slots directly impact, reducing the radiation losses on both sides. Hence, the maximum radiation is in such a way that it is validated by observing the radiation pattern and maximum gain at 4.3 GHz, as demonstrated in Fig. 10.

Fig. 10
figure 10

Radiation pattern distribution at 4.3 GHz (a) without top slots and (b) with top slots

Full size image

As shown in Fig. 11 (a) and (b), the realized gain and the corresponding antenna factor, respectively, in the frequency range (2.4–6 GHz) are increased by more than 2 dB.

Fig. 11
figure 11

Simulation results of (a) The realized gain in dBi with and without triangular slots, and (b) the antenna factor in dBm− 1 with and without triangular slots compared with commercial AF for PowerLOG® PRO 30,800

Full size image

The positions of these slots have been determined using surface current distribution by looking for the electromagnetic waves that do not directly affect the resonance—cutting these parts results in an improvement in the realized gain because it makes the antenna radiation pattern to be more directive.

4 Simulation and Measurement Results

4.1 Reflection Coefficient

The fabrication process has been done in the EMC laboratory at the University of West Bohemia, Faculty of Electrical Engineering, with the help of a ProtoMat S-100 CNC machine. Figure 12(a) presents the fabricated structure of the final design. Furthermore, the S-parameters measurement is performed using RIGOL DSA875 Spectrum Analyzer stands up to 7.5 GHz, as shown in Fig. 12 (b). The simulation and measured results for the reflection coefficient as a function of frequency are shown in Fig. 13, which demonstrates an antenna operational band extends along the range (0.8–5.5 GHz).

Fig. 12
figure 12

Measurement setup of, (a) The fabricated shape of the proposed antenna, and (b) measuring S11 parameter

Full size image
Fig. 13
figure 13

The simulated and measured reflection coefficients for the proposed design versus frequency

Full size image

4.2 Gain and Antenna Factor

The simulated and measured results for the realized gain and corresponding antenna factor are presented in Fig. 14 (a) and (b), respectively. The measured gain was achieved with the help of third antenna (reference antenna with known properties) inside the EMC chamber using the comparison method. This antenna offers good values of antenna factor compared to the commercial antenna, which makes it the right choice to use as a reference antenna.

Fig. 14
figure 14

The simulated and measurement results for the fabricated antenna, (a) the realized gain in dBi versus frequency, (b) the antenna factor in dBm− 1 versus frequency

Full size image

Table 3 lists the achievements of the proposed technique in improving the realized gain compared to the previous articles. It can be seen that the technique used in the proposed structure tackles the aims of size reduction, bandwidth enhancements, and gain improvements. For instance, the proposed work has smaller size compared with ref [34], and ref [34] since they cover the lower frequency band to make fair comparison. Consequently, the proposed method has a considerable gain enhancement of about 3.3 dB at 4.3 GHz with maximum gain of 10.7 dBi compared to the reported literatures. It is worth mentioning that the use of two upside down rectangle slots techniques for gain improvements showed its simplicity and direct influence of enhancing the gain compared to the reported techniques

Table 3 Gain enhancement techniques comparison
Full size table

4.3 Radiation Pattern, Co and Cross-Polarization, and Axial Ratio

The balance or steady phase center is an obligatory specification for every reference antenna. It means that the radiation pattern transition with frequencies must be smooth, and the main-lobe position always stays in the same direction for the whole frequency band. The 3-D radiation patterns for different frequencies are presented in Fig. 15. It is evident that the antenna has a stable radiation pattern by noticing the maximum field’s transition with frequencies. Thus, the antenna can be qualified to serve as a reference antenna. On the other hand, co-polarization and cross-polarization are essential aspects related to the radiation pattern of the proposed antenna in both E-plane and H-plane since the structure is planned to be used as a reference antenna for EMC measurements. The radiation pattern measurement of this antenna has been performed inside the EMC chamber at the University of West Bohemia, Faculty of Electrical Engineering. The proposed antenna is mounted on the turntable and rotated around its axle in both vertical and horizontal direction to record the electric and magnetic field, respectively. “Moreover, the achieved maximum gain has horizontal direction that coincides with the directive Electrical field. Figure 16 shows the co-pol and cross-pol radiation patterns for E & H-plane at different frequencies like 1 GHz, 3 GHz, and 5 GHz. It can be seen that the cross-polarization level starts with small values and then increases with frequency due to the higher mode effect generated by this symmetrical structure. For instance, the cross-polarization component of the E-field begins with − 35 dB at 1 GHz and ends with − 25 dB at 5 GHz. At the same time, the cross-polarization of the H-field starts with − 30 dB at 1 GHz and grows to -15 dB at 5 GHz. It is worth noting that the increase in the cross polarization of the h-plane radiation is due to the undesired radiation modes with increasing frequency. However, the power level of the cross-polarization of the H-field (starts with − 30 dB at 1 GHz and − 15 dB at 5 GHz) does not affect the antenna performances.

Fig. 15
figure 15

The transition of radiation pattern with frequency: (a) 1 GHz, (b) 1.7 GHz, (c) 3 GHz, (d) 5 GHz

Full size image
Fig. 16
figure 16

The simulated and measured results of Co and Cross polarization radiation patterns for both E & H plane, (a) E-field at 1 GHz, (b) E-field at 3 GHz, (c) E-field at 5 GHz, (d) H-field at 1 GHz, (e) H-field at 3 GHz, (f) H-field at 5 GHz

Full size image

The type of polarization is usually demonstrated by presenting an axial ratio (AR) value in dB. For instance, circular polarization has an axial ratio between 0 dB and 3 dB, an axial ratio with a value higher than 3 dB refers to elliptical polarization, and linear polarization is achieved when the AR value goes to infinity. The design of the EMC reference antenna is required to be linearly polarized. However, there will be some deviation between the designer’s goals and the actual realization. The transition region between the linear and elliptical polarization has some ambiguity since infinity is relative, and there is no practical or industrial form to distinguish the boundary between these two types. Furthermore, some references refer that linear polarization is a particular case of elliptical polarization. The proposed design in [38] has demonstrated linear polarization with AR > 10 dB, while authors in [39] have considered AR > 20 dB to be the boundary between linear and elliptical polarization. In this work, the axial ratio has a value of more than 20 dB for the whole frequency band, which indicates the linear polarization that perfectly satisfies the EMC requirement.

4.4 The ∅3dB Beamwidth

Most One of the critical parameters in EMC measurement is the vertical distance w that tangents the DUT, and this distance can be calculated using (6).

$$\:w=2\times\:d\times\:\text{tan}\:\left(0.5\times\:{\varnothing\:}_{3dB}\right)$$
(6)

where d is the minimum measurement distance between the reference antenna and the DUT, which can be either 1 m, 3 m, or 10 m. Table 4 demonstrates the \(\:{\varnothing\:}_{3dB}\) beamwidth and its tangent distance w at minimum measurement distance d = 1 m for both Vivaldi antenna and the DRG Horn antenna of CISPR standard [40]. The half-power beamwidth angles for the proposed structure are agreeable with the CISPR standard.

Table 4 Illustrates the comparison of beamwidth angles of the proposed antenna with the DRG horn antenna of CISPR standard
Full size table

4.5 Comparison with the Commercial Antenna PowerLOG® PRO 30,800 and TBMA4

A comparison between the specifications of the proposed antenna and the commercial antennas offered for sale [41] and [42] is listed in Table 5. The calibrated antenna PowerLOG® PRO 30,800 has relative bandwidth of 180% with a size of 510 × 507 × 507 mm3 while EMC antenna type TBMA4 shows a relatively small size of 241 × 214 × 153 mm3 with relative bandwidth of 155%. In comparison, the proposed antenna offers a relative bandwidth of 150% with a compact and low-profile size of 180 × 165 × 1.6 mm3. The size reduction of the proposed antenna in both length and width are 64% and 67% compared to the PowerLOG® PRO 30,800 antenna and 25% and 22% compared to the TBMA4 antenna. Furthermore, the gain of both structures is relatively good for EMC measurements reflecting good antenna factor values.

Table 5 Comparison between the proposed design specifications and the PowerLOG® PRO 30,800 and TBMA4 antenna designs offered for sale
Full size table

The numerical values of antenna factor versus frequency for the proposed structure, Ref [16], and the commercial antennas offered for sale are listed in Table 6. It is clear that the proposed antenna has a promising antenna factor making it a good candidate to serve as a reference antenna inside the EMC chamber.

Table 6 Numerical values of antenna factor versus frequency
Full size table

The proposed structures in the referenced papers [2,3,4] and [39] were compared with their equivalent classical structures to show their performance and their advantages in terms of size reduction, bandwidth enhancement, gain, antenna factor, and radiation pattern. Consequently, the achieved results in the proposed work are significant w.r.t references [2,3,4] and [39]. For instance, the proposed antenna has a high gain of about 10.7 dBi compared to the cited papers, where the high value of gain reflects good antenna factor (in terms of stability and un uncertainty) and makes it applicable to use for radiated emission and radiated immunity test. Furthermore, the size reduction of this antenna is 64% and 67% compared to the classical horn antenna used for the same purpose. And finally, the use of two upside down rectangle slots techniques for gain improvements showed its simplicity and direct influence on enhancing the gain compared to the reported techniques in Table 3. It is worth mentioning that the proposed structure could be modified to exhibit a dual-polarized Vivaldi antenna for future work with appropriate calibration”.

5 Conclusion

A compact Vivaldi slot antenna has been designed, modeled, and fabricated to serve as a reference antenna inside an EMC chamber. The structure has been fed by the electromagnetic coupling method with an open circuit radial stub which results in impedance bandwidth from 0.8 GHz to 5.5 GHz. The proposed antenna realized gain, and antenna factor are high enough to mitigate the noise measurement at microwave frequencies. The gain at low frequencies has been improved by using two horizontal rectangular slots. Then two reversed triangular slots were utilized to enhance the antenna gain at the high-frequency bands with a 3.5 dB improvement at 4.3 GHz. The specifications of the proposed structure have been compared with the calibrated commercial Horn antenna offered for sale. In conclusion, this antenna can be utilized as a reference due to its good specifications in terms of compact size (size reduction in both length and width are 64% and 67%), wide bandwidth (150% relative bandwidth), stable radiation pattern, and good antenna factor. Moreover, the proposed structure could be modified to exhibit a dual-polarized Vivaldi antenna for future work with appropriate calibration.