Joint Beamforming and Power Control for Downlink Multi-cell Massive MIMO System | Wireless Personal Communications Skip to main content
Springer Nature Link
Log in

Joint Beamforming and Power Control for Downlink Multi-cell Massive MIMO System

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

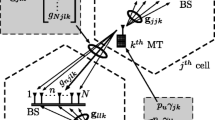
This paper is concerned with joint beamforming and power control for downlink multi-cell massive multiple-input and multiple-output system. The finite system analysis and large system analysis are successively made for two different system configurations. When base station (BS) antenna number and user number per cell are not large, the finite system analysis of single cell is extended to the multi-cell case after problem reformulation. With the Perron–Frobenius theory and alternative optimization, the dual uplink power and beamformers can be calculated iteratively. Based on the iteration result and the uplink-downlink duality, the final solution is obtained. However, when BS antenna number and user number are large, the large system analysis is employed. In order to reduce computation complexity, the dual uplink power is approximated by its asymptotic equivalent. First, the asymptotic expression of signal to interference plus noise ratio is derived via random matrix theory. Next, the power control problem is reformulated in the asymptotic regime to obtain the asymptotic dual uplink power. As the asymptotic dual uplink power only depends on the second order statistic, it does not require updating along with the channel state information instantaneously. As a result, the computation complexity is drastically reduced.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Andrews, J. G., Buzzi, S., Wan, C., Hanly, S. V., Lozano, A., Soong, A. C. K., et al. (2014). What will 5G be? IEEE Journal on Selected Areas in Communications,32(6), 1065–1082.

    Article  Google Scholar 

  2. Lu, L., Li, G. Y., Swindlehurst, A. L., Ashikhmin, A., & Zhang, R. (2014). An overview of massive MIMO: Benefits and challenges. IEEE Journal of Selected Topics in Signal Processing,8(5), 742–758.

    Article  Google Scholar 

  3. Lakshminaryana, S., Hoydis, J., Debbah, M., & Assaad, M. (2010). Asymptotic analysis of distributed multi-cell beamforming. In Annual IEEE international symposium on personal, indoor and mobile radio communications, Instanbul, Turkey, 26–30 September 2010 (pp. 2105–2110). https://doi.org/10.1109/pimrc.2010.5671653.

  4. Dahrouj, H., & Yu, W. (2010). Coordinated beamforming for the multicell multi-antenna wireless system. IEEE Transactions on Wireless Communications,9(5), 1748–1759. https://doi.org/10.1109/TWC.2010.05.090936.

    Article  Google Scholar 

  5. Pennanen, H., Tolli, A., & Latva-aho, M. (2011). Decentralized coordinated downlink beamforming via primal decomposition. IEEE Signal Processing Letters,18(11), 647–650. https://doi.org/10.1109/LSP.2011.2168206.

    Article  Google Scholar 

  6. Tolli, A., Pennanen, H., & Komulainen, P. (2011). Decentralized minimum power multi-cell beamforming with limited backhaul signaling. IEEE Transactions on Wireless Communications,10(2), 570–580. https://doi.org/10.1109/TWC.2011.120810.100363.

    Article  Google Scholar 

  7. Lakshminarayana, S., Assaad, M., & Debbah, M. (2015). Coordinated multicell beamforming for massive MIMO: A random matrix approach. IEEE Transactions on Information Theory,61(6), 3387–3412. https://doi.org/10.1109/TIT.2015.2421446.

    Article  MathSciNet  MATH  Google Scholar 

  8. Asgharimoghaddam, H., Tölli, A., & Rajatheva, N. (2014). Decentralizing the optimal multi-cell beamforming via large system analysis. In IEEE international conference on communications, Sydney, Australia, 10–14 June 2014 (pp. 5125–5130). https://doi.org/10.1109/icc.2014.6884134.

  9. Sanguinetti, L., Björnson, E., Debbah, M., & Moustakas, A. L. (2014). Optimal linear precoding in multi-user MIMO systems: A large system analysis. In IEEE global communications conference, Austin, USA, 8–12 December 2014 (pp. 3922–3927). https://doi.org/10.1109/glocom.2014.7037420.

  10. Schubert, M., & Boche, H. (2004). Solution of the multiuser downlink beamforming problem with individual SINR constraints. IEEE Transactions on Vehicular Technology,53(1), 18–28. https://doi.org/10.1109/TVT.2003.819629.

    Article  Google Scholar 

  11. Huang, Y., Tan, C. W., & Rao, B. D. (2013). Joint beamforming and power control in coordinated multicell: Max–min Duality, effective network and large system transition. IEEE Transactions on Wireless Communications,12(6), 2730–2742. https://doi.org/10.1109/TWC.2013.042313.120752.

    Article  Google Scholar 

  12. Seneta, E. (1981). Non-negative matrices and markov chains. New York: Springer.

    Book  Google Scholar 

  13. Cai, D. W. H., Quek, T. Q. S., Tan, C. W., & Low, S. H. (2012). Max–min SINR coordinated multipoint downlink transmission—duality and algorithms. IEEE Transactions on Signal Processing,60(10), 5384–5395. https://doi.org/10.1109/TSP.2012.2208631.

    Article  MathSciNet  MATH  Google Scholar 

  14. Schubert, M., & Boche, H. (2002). A unifying theory for uplink and downlink multiuser beamforming. In International Zurich seminar on broadband communications access: Transmission—networking, Zurich, Switzerland, 2002 (pp. 27-21–27-26). https://doi.org/10.1109/izsbc.2002.991770.

  15. Tse, D. N. C., & Hanly, S. V. (1999). Linear multiuser receivers: Effective interference, effective bandwidth and user capacity. IEEE Transactions on Information Theory,45(2), 641–657. https://doi.org/10.1109/18.749008.

    Article  MathSciNet  MATH  Google Scholar 

  16. Assche, W. V. (1987). Asymptotics for orthogonal polynomials. Heidelberg: Springer.

    Book  Google Scholar 

  17. Yates, R. D. (1995). A framework for uplink power control in cellular radio systems. IEEE Journal on Selected Areas in Communications,13(7), 1341–1347. https://doi.org/10.1109/49.414651.

    Article  Google Scholar 

  18. Krause, U. (2001). Concave Perron–Frobenius theory and applications. Nonlinear Analysis,47(3), 1457–1466.

    Article  MathSciNet  Google Scholar 

  19. Blondel, V. D., Ninove, L., & Dooren, P. V. (2005). An affine eigenvalue problem on the nonnegative orthant. Linear Algebra and Its Applications,404(2), 69–84.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported by “Beijing Key Laboratory of Work Safety Intelligent Monitoring (Beijing University of Posts and Telecommunications)”.

Author information

Authors and Affiliations

  1. School of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing, China

    Yunxiao Zu, Lin Shao & Bin Hou

Authors
  1. Yunxiao Zu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lin Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bin Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yunxiao Zu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zu, Y., Shao, L. & Hou, B. Joint Beamforming and Power Control for Downlink Multi-cell Massive MIMO System. Wireless Pers Commun 111, 245–266 (2020). https://doi.org/10.1007/s11277-019-06855-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-019-06855-4

Keywords

Search

Navigation