Research on the Hash Function Structures and its Application | Wireless Personal Communications Skip to main content
Springer Nature Link
Log in

Research on the Hash Function Structures and its Application

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

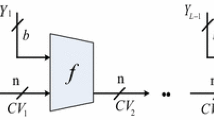
Abstract

Since the traditional classic hash function structure (MD structure) is suffering from all kinds of attacks, the research of new hash function structure becomes hot issue. This paper analyses these attacks, based on MD structure, this paper brings in two security parameters and improves the message padding scheme, and then designs a Double-Serial iterative structure. In this structure, since there are more message blocks affecting the chaining variables, it can not only avoid the traditional second collision attack, multicollision attack and second preimage attack of long message, but also accelerate the message diffusion and enhance the avalanche effect. According to the efficiency analysis and security authentication, this proposed structure improves security and has the same efficiency of Double-Pipe structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Wang X., Feng D., & Lai X. (2004) Collisions for some hash functions MD4, MD5, HAVAL-128, RIPEMD. Cryptology ePrint Archive, Report 2004/199. http://eprint.iacr.org/2004/199.pdf.

  2. Boer B. D., & Bosselaers A. (1994). Collisions for the compression function of MD5. Eurocrypt 1993, LNCS 765, pp. 293–304.

  3. Dobbertin H. (2001). Cryptanalysis of MD5 compress. In Advances in Cryptology, Eurocrypt’96 Rump Session (Vol. 11, pp. 253–271).

  4. Chabaud F., & Joux A. (1998) Differential collisions in SHA-0. Crypto 1998, LNCS 1462, pp. 56–71.

  5. Lucks S. (2005). A failure-friendly design principle for hash functions. Asiacrypt 2005, LNCS 3788 pp. 474–494.

  6. Rivest R. L. (2005). Abelian square-free dithering for iterated hash functions. Presented at ECryt Hash Function Workshop. June, 2005, Cracow.

  7. Biham E., Dunkelman O. (2007). A framework for iterative hash functions—HAIFA. Cryptology ePrint Archive: Report 2007/278.

  8. Bertoni G., Daeman J., Peeters M., & Assche G. V. (2007). Sponge functions. ECRYPT Hash Workshop 2007. http://www.csrc.nist.gov/pki/HashWorkshop/PublicComments/2007May.html.

  9. Tiwari, H., & Asawa, K. (2012). A secure and efficient cryptographic hash function based on NewFORK-256. Egyptian Informatics Journal, 13, 199–208.

    Article  Google Scholar 

  10. Yantao, L., Xiang, L., Xiangwei, L. (2016). A fast and efficient hash function based on generalized chaotic mapping with variable parameters. Neural Computing Applications. doi:10.1007/s00521-015-2158-7.

  11. Yantao, L. (2016). Collision analysis and improvement of a hash function based on chaotic tent map. Optik, 127, 4484–4489.

    Article  Google Scholar 

  12. Ping, Z., Geng, Z., Lequan, M., & Xiaodong, L. (2014). Novel hash function based on coupled chaotic map lattice. Chinese Journal of Electronics, 23(4), 836–841.

    Google Scholar 

  13. Abdulaziz, M., Khalil, I., Imad, F., & Mohammad, A. (2015). A new design of cryptographic hash function: gear. International Journal on Perceptive and Cognitive Computing, 1(1), 29–34.

    Google Scholar 

Download references

Acknowledgments

This work was supported by the National Nature Science Foundation of China under Grant 61502314, 61171072, and the Science and Technology Projects of Shenzhen (JCYJ20130329115832637 and ZDSYS20140430164957660), Tencent Rhinoceros Birds Scientific Research Foundation (2015), the Technology Planning Project (Grant No. 2014B010118005) from Guangdong Province, China, the Science and Technology Plan Projects of Shenzhen (JCYJ 20150324140036830, JCYJ 20160307115030281, 20160224144857159).

Author information

Authors and Affiliations

  1. College of Computer and Software Engineering, Shenzhen University, Shenzhen, 518060, Guangdong, China

    Yijun Yang & Fei chen

  2. Key Laboratory of Optoelectronic Devices and System of Ministry of Education and Guangdong Province, College of Optoelectronic Engineering, Shenzhen University, Shenzhen, 518060, Guangdong, China

    Yijun Yang

  3. College of Information Engineering, Shenzhen University, Shenzhen, 518060, Guangdong, China

    Xiaomei Zhang, Jianping Yu & Peng Zhang

Authors
  1. Yijun Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fei chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xiaomei Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jianping Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Peng Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Peng Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Y., chen, F., Zhang, X. et al. Research on the Hash Function Structures and its Application. Wireless Pers Commun 94, 2969–2985 (2017). https://doi.org/10.1007/s11277-016-3760-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-016-3760-4

Keywords