Analysis of Link Life Time in Vehicular Ad Hoc Networks for Free-Flow Traffic State

Abstract

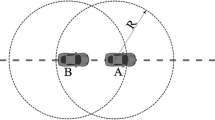
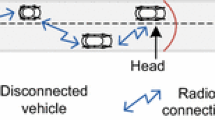
In this paper, we present analytical models for the probability density function (PDF) of link life time in vehicular ad hoc networks (VANETs), formed on both single lane as well as multi lane highways. Assuming free flow traffic state and Gaussian distributed vehicle speed, we extensively investigate the impact of vehicle mobility, vehicle density and transmission range on the link life time PDF and the mean link life time in VANETs. Our analytical and simulation results suggest that in the free-flow traffic state, exponential distribution with appropriate parametrization is a good approximation for the link life time PDF. We perform the Kolmogorov–Smirnov goodness-of-fit test to ascertain the validity of this claim.

Appendices

Appendix 1

Derivation of (7) and (8):

Since the link life time $T^{(0)}$ is given by (5), its CDF $F_{T^{(0)}}(t)$ can be determined as follows:

$$\begin{aligned} F_{T^{(0)}}(t)=P(T^{(0)}\le t) =P(X\le V_r^{(0)} t) \end{aligned}$$

(16)

Using the principle of random variable transformation and by referring to Figs. 14 and 15, $F_{T^{(0)}}(t)$ can be determined as follows:

$$\begin{aligned} F_{T^{(0)}}(t)=\left\{ \begin{array}{l@{\quad }l} 2\int _{v_r^{(0)} = 0}^{v_m} \! \int _{x = -R}^{v_r^{(0)} t} \! f_{X,V_r^{(0)}}(x,v_r^{(0)}) \,~\mathrm d x \,~\mathrm d v_r^{(0)}; &{} t\le \frac{R}{v_m}\\ 2\int _{v_r^{(0)} = 0}^{v_m} \! \int _{x = -R}^{v_r^{(0)} t} \! f_{X,V_r^{(0)}}(x,v_r^{(0)}) \,~\mathrm d x \,~\mathrm d v_r^{(0)} \\ - 2 \int _{v_r^{(0)} = R/t}^{v_m} \! \int _{x = R}^{v_r^{(0)} t} \! f_{X,V_r^{(0)}}(x,v_r^{(0)}) \,~\mathrm d x \,~\mathrm d v_r^{(0)}; &{} t> \frac{R}{v_m} \end{array}\right. \end{aligned}$$

(17)

The PDF of $T^{(0)}$, $f_{T^{(0)}}(t)$ is obtained by differentiating 17 with respect to $t$ and is given by:

$$\begin{aligned} f_{T^{(0)}}(t)=\left\{ \begin{array}{l@{\quad }l} f_{T_1^{(0)}}(t);&{}t\le \frac{R}{v_m} \\ f_{T_1^{(0)}}(t)-f_{T_2^{(0)}}(t) ;&{}t> \frac{R}{v_m} \\ \end{array}\right. \end{aligned}$$

(18)

where the components $f_{T_1^{(0)}}(t)$ and $f_{T_2^{(0)}}(t)$ correspond to the following two cases.

Fig. 14

Finding $F_{T^{(0)}}(t)$ (Case i)

Fig. 15

Finding $F_{T^{(0)}}(t)$ (Case ii)

Case i: $t\le R/v_m$

Since $X$ and $V_r^{(0)}$ are independent random variables, $f_{T^{(0)}}(t)$ can be determined by substituting (4) and (6) in (17) and is given by the following expression represented as $f_{T_1^{(0)}}(t)$:

$$\begin{aligned} f_{T_1^{(0)}}(t)&= 2\frac{2\rho / (\sigma _r \sqrt{2 \pi })}{erf(\frac{v_m-\mu _r}{\sigma _r\sqrt{2}})-erf(\frac{-v_m-\mu _r}{\sigma _r\sqrt{2}})} \frac{d}{dt} \int \limits _{v_r^{(0)} = 0}^{v_m} \,\, \int \limits _{x = -R}^{v_r^{(0)} t} \! e^{-\rho x} e^\frac{-(v_r^{(0)}-\mu _r)^2}{2\sigma _r^2}~\mathrm d x \,~\mathrm d v_r^{(0)} \nonumber \\ \end{aligned}$$

(19)

The above integral can be simplified to get the following expression for $f_{T_1^{(0)}}(t)$:

$$\begin{aligned} f_{T_1^{(0)}}(t)&= 2\frac{\frac{2\rho }{\sigma _r \sqrt{2\pi }} e^{\frac{-\mu _r^2}{2\sigma _r^2}}e^{\frac{{(\mu _r - \rho t \sigma _r^2)}^2}{2\sigma _r^2}}}{erf(\frac{v_m - \mu _r}{\sqrt{2}\sigma _r}) - erf (\frac{-v_m-\mu _r}{\sqrt{2}\sigma _r})}\left[ \sigma _r^2 \left( e^{\frac{{-(\mu _r - \rho t \sigma _r^2)}^2}{2\sigma _r^2}} - e^{\frac{-(v_m - (\mu _r - \rho t \sigma _r^2))^2}{2\sigma _r^2}}\right) \right. \nonumber \\&\quad +\left. \sqrt{\frac{\pi }{2}}(\mu _r - \rho t \sigma _r ^2) \sigma _r \left( erf\left( \frac{v_m - (\mu _r - \rho t \sigma _r ^ 2)}{\sqrt{2} \sigma _r}\right) + erf\left( \frac{(\mu _r-\rho t \sigma _r^2)}{\sqrt{2}\sigma _r}\right) \right) \right] \nonumber \\ \end{aligned}$$

(20)

Case ii: when $t>R/v_m$.

In this case, $f_{T^{(0)}}(t)$ is obtained by subtracting a component $f_{T_2^{(0)}}(t)$ from (20). Now $f_{T_2^{(0)}}(t)$ is determined by utilizing (4), (6) and (17):

$$\begin{aligned} f_{T_2^{(0)}}(t)&= 2 \frac{d}{dt} \int \limits _{v_r^{(0)} = R/t}^{v_m}\,\, \int \limits _{x = R}^{v_r^{(0)} t} \! f_{X}(x)f_{V_r^{(0)}}(v_r^{(0)}) \,~\mathrm d x~\mathrm d v_r \nonumber \\&= 2\frac{2\rho / (\sigma _r \sqrt{2 \pi )}}{erf(\frac{v_m-\mu _r}{\sigma _r\sqrt{2}})-erf(\frac{-v_m-\mu _r}{\sigma _r\sqrt{2}})}\frac{d}{dt} \int \limits _{v_r^{(0)} = R/t}^{v_m} \,\, \int \limits _{x = R}^{v_r^{(0)} t} \! e^{-\rho x} e^\frac{-(v_r^{(0)}-\mu _r)^2}{2\sigma _r^2} ~\mathrm d x~\mathrm d v_r^{(0)}\qquad \quad \end{aligned}$$

(21)

Notice that (21) can be simplified to get the following expression for $f_{T_2^{(0)}}(t)$:

$$\begin{aligned} f_{T_2^{(0)}}(t)&= 2 \frac{\frac{2}{\sigma _r \sqrt{2\pi }}}{erf(\frac{v_m-\mu _r}{\sigma _r \sqrt{2}}-erf(\frac{-v_m-\mu _r}{\sigma _r \sqrt{2}})} \left[ \left( e^{-\rho R}R/t^2 e^\frac{-(R/t-\mu _r)^2}{2\sigma _r^2}\right) \right. \nonumber \\&\quad - \sqrt{\pi /2}\sigma _r e^\frac{-2\mu _r\rho t \sigma _r^2 +\rho ^2t^2\sigma _r^4}{2\sigma _r} \left( \Bigg (-\mu _r\rho +\rho ^2t\sigma _r^2\Bigg ) \left( erf\frac{v_m-(\mu _r-\rho t\sigma _r^2)}{\sqrt{2}\sigma _r^2}\right. \right. \nonumber \\&\quad -\left. erf\frac{R/t-(\mu _r-\rho t\sigma _r^2)}{\sqrt{2}\sigma _r^2} \right) + \left( \sqrt{2/\pi }\rho \sigma _r e^\frac{-(v_m-(\mu _r-\rho t \sigma _r^2)^2}{2\sigma _r^2}\right. \nonumber \\&\quad -\left. \left. \left. \sqrt{2/\pi } e^\frac{-(R/t-(\mu _r-\rho t \sigma _r^2)^2}{2\sigma _r^2}\frac{-R/t^2 +\rho \sigma _r^2}{\sigma _r}\right) \right) \right] \end{aligned}$$

(22)

Accordingly, when $t\le R/v_m$, the PDF of $T^{(0)}$, $f_{T^{(0)}}(t)$ is given by (20), whereas, when $t>R/v_m$, $f_{T^{(0)}}(t)$ is determined by subtracting (22) from (20).

Appendix 2

Derivation of (13) and (14):

To derive (13) and (14), we follow the approach similar to the one used for the derivation of (7) and (8) in Appendix A. The link duration $T^{(1)}$ is given by (12). By following an approach similar to (17) , the CDF of $T^{(1)}$, $F_{T^{(1)}}(t)$ can be written as follows:

$$\begin{aligned} F_{T^{(1)}}(t)=\left\{ \begin{array}{l@{\quad }l} 2\int _{v_r^{(1)} = 0}^{v_2} \! \int _{y = -R\cos \beta }^{v_r^{(1)} t} \! f_{Y,V_r^{(1)}}(y,v_r^{(1)}) \,~\mathrm d y \,~\mathrm d v_r^{(1)} ;&{} t\le \frac{R\cos \beta }{v_2}\\ 2\int _{v_r^{(1)} = 0}^{v_2} \! \int _{y = -R\cos \beta }^{v_r^{(1)} t} \! f_{Y,V_r^{(1)}}(y,v_r^{(1)}) \,~\mathrm d y \,~\mathrm d v_r^{(1)} \\ - 2 \int _{v_r^{(1)} = R\cos \beta /t}^{v_2} \! \int _{y = R\cos \beta }^{v_r^{(1)} t} \! f_{Y,V_r^{(1)}}(y,v_r^{(1)}) \,~\mathrm d y \,~\mathrm d v_r^{(1)}; &{} t> \frac{R\cos \beta }{v_2} \\ \end{array}\right. \end{aligned}$$

(23)

The PDF of $T^{(1)}$, $f_{T^{(1)}}(t )$ is obtained by differentiating (23) w.r.t $t$ and is represented as follows:

$$\begin{aligned} f_T^{(1)}(t)=\left\{ \begin{array}{l@{\quad }l} f_{T_1^{(1)}}(t) ;&{}t\le \frac{R\cos \beta }{v_2} \\ f_{T_1^{(1)}}(t)-f_{T_2^{(1)}}(t) ;&{}t> \frac{R\cos \beta }{v_2} \\ \end{array}\right. \end{aligned}$$

(24)

where $f_{T_1^{(1)}}(t)$ and $f_{T_2^{(1)}}(t)$ are determined as follows:

Case i: $t\le R\cos \beta /v_2$.

Here the PDF of $T^{(1)}$, represented as $f_{T_1^{(1)}}(t)$ in (24) is obtained by following an approach similar to the one used for the derivation of (20). Assuming that $Y$ and $V_r^{(1)}$ are independent and substituting (10) and (11) in (23), and after further algebraic simplification, we get:

$$\begin{aligned} f_{T_1^{(1)}}(t)&= 2\frac{2\rho / (\sigma _r \sqrt{2 \pi })}{erf(\frac{v_2-\mu _r}{\sigma _r\sqrt{2}})-erf(\frac{v_1-\mu _r}{\sigma _r\sqrt{2}})} \frac{d}{dt} \int \limits _{v_r^{(1)} = 0}^{v_2} \! \int \limits _{y = -R\cos \beta }^{v_r^{(1)} t} \! e^{-\rho y} e^\frac{-(v_r^{(1)}-\mu _r)^2}{2\sigma _r^2}~\mathrm d y \,~\mathrm d v_r^{(1)} \nonumber \\&= 2\frac{\frac{2\rho }{\sigma _r \sqrt{2\pi }} e^{\frac{-\mu _r^2}{2\sigma _r^2}}e^{\frac{{(\mu _r - \rho t \sigma _r^2)}^2}{2\sigma _r^2}}}{erf(\frac{v_2 - \mu _r}{\sqrt{2}\sigma _r}) - erf (\frac{v_1-\mu _r}{\sqrt{2}\sigma _r})}\left[ \sigma _r^2 \left( e^{\frac{{-(\mu _r - \rho t \sigma _r^2)}^2}{2\sigma _r^2}} - e^{\frac{-(v_2 - (\mu _r - \rho t \sigma _r^2))^2}{2\sigma _r^2}}\right) \right. \nonumber \\&\quad +\left. \sqrt{\frac{\pi }{2}}(\mu _r - \rho t \sigma _r ^2) \sigma _r \left( erf\left( \frac{v_2 - (\mu _r - \rho t \sigma _r ^ 2)}{\sqrt{2} \sigma _r}\right) + erf\left( \frac{(\mu _r-\rho t \sigma _r^2)}{\sqrt{2}\sigma _r}\right) \right) \right] \nonumber \\ \end{aligned}$$

(25)

Case ii: $t>R\cos \beta /v_2$.

Here the PDF of $T^{(1)}$, $f_{T^{(1)}}(t)$ consist of two terms: $f_{T_1^{(1)}}(t)$ and $f_{T_2^{(1)}}(t)$. Now $f_{T_1^{(1)}}(t)$ is given by (25). The term $f_{T_2^{(1)}}(t)$ is obtained by substituting (10) and (11) in (23) and is given by:

$$\begin{aligned} f_{T_2^{(1)}}(t)&= 2\frac{2\rho / (\sigma _r \sqrt{2 \pi )}}{erf(\frac{v_2-\mu _r}{\sigma _r\sqrt{2}})-erf(\frac{v_1-\mu _r}{\sigma _r\sqrt{2}})}\frac{d}{dt} \int \limits _{v_r^{(1)} = R\cos \beta /t}^{v_2} \! \int \limits _{y = R\cos \beta }^{v_r^{(1)} t} \! e^{-\rho y} e^\frac{-(v_r^{(1)}-\mu _r)^2}{2\sigma _r^2} ~\mathrm d y~\mathrm d v_r^{(1)} \nonumber \\&= 2 \frac{\frac{2}{\sigma _r \sqrt{2\pi }}}{erf(\frac{v_2-\mu _r}{\sigma _r \sqrt{2}})-erf(\frac{v_1-\mu _r}{\sigma _r \sqrt{2}})} \left[ \left( e^{-\rho R\cos \beta }R\cos \beta /t^2 e^\frac{-(R\cos \beta /t-\mu _r)^2}{2\sigma _r^2}\right) \right. \nonumber \\&\quad - \sqrt{\pi /2}\sigma _r e^\frac{-2\mu _r\rho t \sigma _r^2 +\rho ^2t^2\sigma _r^4}{2\sigma _r} \left( \Big (-\mu _r\rho +\rho ^2t\sigma _r^2\Big ) \left( erf\frac{v_2-(\mu _r-\rho t\sigma _r^2)}{\sqrt{2}\sigma _r^2}\right. \right. \nonumber \\&\quad -\left. erf\frac{R\cos \beta /t-(\mu _r-\rho t\sigma _r^2)}{\sqrt{2}\sigma _r^2} \right) + \left( \sqrt{2/\pi }\rho \sigma _r e^\frac{-(v_2-(\mu _r-\rho t \sigma _r^2)^2}{2\sigma _r^2}\right. \nonumber \\&\quad -\left. \left. \left. \sqrt{2/\pi } e^\frac{-(R\cos \beta /t-(\mu _r-\rho t \sigma _r^2)^2}{2\sigma _r^2}\frac{-R\cos \beta /t^2 +\rho \sigma _r^2}{\sigma _r}\right) \right) \right] \end{aligned}$$

(26)

When $t\le R/v_2$, the PDF of $T^{(1)}$, $f_{T^{(1)}}(t)$ is given by (25), whereas when $t>R/v_2$, $f_{T^{(1)}}(t)$ is obtained by subtracting (26) from (25).