Efficient Systolic Designs for 1- and 2-Dimensional DFT of General Transform-Lengths for High-Speed Wireless Communication Applications | Journal of Signal Processing Systems Skip to main content
Springer Nature Link
Log in

Efficient Systolic Designs for 1- and 2-Dimensional DFT of General Transform-Lengths for High-Speed Wireless Communication Applications

  • Published:
Journal of Signal Processing Systems Aims and scope Submit manuscript

Abstract

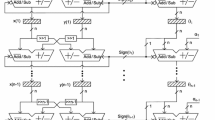
In wireless communication, multiple receive-antennas are used with orthogonal frequency division multiplexing (OFDM) to improve the system capacity and performance. The discrete Fourier transform (DFT) plays an important part in such a system since the DFTs are required to be performed for the output of all those antennas separately. This paper presents area-time efficient systolic structures for one-dimensional (1-D) and two-dimensional (2-D) DFTs of general lengths. A low-complexity recursive algorithm based on Clenshaw’s recurrence relation is formulated for the computation of 1-D DFT. The proposed algorithm is used further to derive a linear systolic array for the DFT. The concurrency of computation has been enhanced and complexity is minimized by the proposed algorithm where an N −point DFT is computed via four inner-products of real-valued data of length ≈ (N/2). The proposed 1-D structure offers significantly lower latency, twice the throughput, and involves nearly the same area-time complexity of the corresponding existing structures. The proposed algorithm for 1-D DFT is extended further to obtain a 2-D systolic structure for the 2-D DFT without involving any transposition operation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6

Similar content being viewed by others

Notes

  1. The average computation-time (ACT) is the time-interval between the completion of the computation of the DFT of two successive blocks of input. ACT can be estimated as (N/throughput) in case of 1-D DFT and (N 2/throughput) in case of 2-D DFT.

References

  1. Bracewell, R. N. (2000). The Fourier transform and its applications (3rd ed.). Boston: McGraw-Hill.

    Google Scholar 

  2. Wong, K. K., Cheng, R. S. K., Letaief, K. B., & Murch, R. D. (2001). Adaptive antennas at the mobile and base stations in an OFDM/TDMA system. IEEE Transactions on Communications, 49(1), 195–206.

    Article  MATH  Google Scholar 

  3. Grass, E., et al. (2001). On the single-chip implementation of a hiperlan/2 and IEEE 802.11a capable modem. IEEE Personal Communications, 8(6), 48–57.

    Article  Google Scholar 

  4. Mahesh, R., & Vinod, A. P. (2008). Coefficient decimation approach for realizing reconfigurable finite impulse response filters. In Proc. IEEE international symposium on circuits & systems, ISCAS ’08 (pp. 81–84), May.

  5. Duhamel, P., & Vetterli, M. (1990). Fast Fourier transforms: A tutorial review and a state of the art. IEEE Transactions on Signal Processing, 19, 259–299.

    MATH  MathSciNet  Google Scholar 

  6. Sundararajan, D., Ahmad, M. O., & Swamy, M. N. S. (1998). Vector computation of the discrete Fourier transform. IEEE Transactions on Circuits and Systems. II: Analog and Digital Signal Processing, 45(4), 449–461.

    Article  MATH  Google Scholar 

  7. Silverman, H. (1977). An introduction to programming the Winograd Fourier transform algorithm (WFTA). IEEE Transactions on Acoustics, Speech, and Signal Processing, 25(2), 152–165.

    Article  MATH  Google Scholar 

  8. Swartzlander, Jr., E. E. (1986). VLSI signal processing systems. Boston: Kluwer.

    MATH  Google Scholar 

  9. Kung, S. Y. (1988). VLSI array processors. Englewood Cliffs: Prentice Hall.

    Google Scholar 

  10. Guo, J.-I., Liu, C.-M., & Jen, C.-W. (1992). The efficient memory-based VLSI array design for DFT and DCT. IEEE Transactions on Circuits and Systems. II: Analog and Digital Signal Processing, 39(10), 723–733.

    Article  MATH  Google Scholar 

  11. Canaris, J. (1993). A VLSI architecture for the real time computation of discrete trigonometric transforms. Journal of VLSI Signal Processing, 5, 95–104.

    Article  MATH  Google Scholar 

  12. Kung, H. T. (1982). Why systolic architectures? IEEE Computer, 15, 37–45.

    Google Scholar 

  13. Chang, C. H., Wang, C. L., & Chang, Y. T. (2000). Efficient VLSI architectures for fast computation of the discrete Fourier transform and its inverse. IEEE Transactions on Signal Processing, 48(11), 3206–3216.

    Article  MATH  Google Scholar 

  14. Hsiao, S. F., & Shiue, W. R. (2000). Low-cost unified architectures for the computation of discrete trigonometric transforms. In Proc. IEEE international conf. on acoust. speech. and signal process (ICASSP ’2000) (Vol. 6, pp. 3299–3302), June.

  15. Jones, K. J. (1990). High-throughput, reduced-hardware systolic solution to prime factor discrete Fourier transform algorithm. IEE Proceedings E. Computers and Digital Techniques, 137(3), 191–196.

    Google Scholar 

  16. Sediljom, S. G. (1994). A new systolic architecture for pipeline prime factor DFT-algorithm. In Proc. fourth great lakes symp on design automation of high performance VLSI systems (pp. 40–45), March.

  17. Lim, H., & Swartzlander, Jr., E. E. (1999). Multidimensional systolic arrays for the implementation of discrete Fourier transforms. IEEE Transactions on Signal Processing, 47(5), 1359–1370.

    Article  Google Scholar 

  18. Nash, J. G. (2005). Computationally efficient systolic architecture for computing the discrete Fourier transform. IEEE Transactions on Signal Processing, 53(12), 4640–4651.

    Article  MathSciNet  Google Scholar 

  19. Nash, J. (2002). Hardware efficient base-4 systolic architecture for computing the discrete Fourier transform. In Proc. IEEE workshop on signal processing systems (SiPS ’02) (pp. 87–92), May.

  20. Baghaie, R., & Hartimo, I. (1993). An efficient new systolic architecture for the solution of discrete Fourier transform. In Proc. VI workshop on VLSI signal processing (pp. 453–461), October.

  21. Wang, L., Hartimo, I., & Laakso, T. (1992). A novel double-decomposition method for systolic implementation of DFT. In Proceedings of IEEE international symposium on circuits and systems (ISCAS ’92) (Vol. 3, pp. 1085–1088), May.

  22. Kar, D. C., & Rao, V. V. B. (1993). A new systolic realization for the discrete Fourier transform. IEEE Transactions on Signal Processing, 41(5), 2008–2010.

    Article  MATH  Google Scholar 

  23. Murthy, N. R., & Swamy, M. N. S. (1994). On the real-time computation of DFT and DCT through systolic architectures. IEEE Transactions on Signal Processing, 42(4), 988–991.

    Article  Google Scholar 

  24. Liu, C. M., & Jen, C. W. (1992). On the design of VLSI arrays for discrete Fourier transform. IEE Proceedings G. Circuits, Devices and Systems, 139(4), 541–552.

    Article  Google Scholar 

  25. Fang, W. H., & Wu, M. L. (1997). An efficient unified systolic architecture for the computation of discrete trigonometric transforms. In Proc. IEEE symp. circuits and syst. (Vol. 3, pp. 2092–2095).

  26. Fang, W. H., & Wu, M. L. (1999). Unified fully-pipelined implementations of one- and two-dimensional real discrete trigonometric transforms. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Science, E82-A(10), 2219–2230, October.

    MathSciNet  Google Scholar 

  27. Chang, T. S., Guo, J. I., & Jen, C. W. (2000). Hardware-efficient DFT designs with cyclic convolution and subexpression sharing. IEEE Transactions on Circuits and Systems. II: Analog and Digital Signal Processing, 47(9), 886–892.

    Article  Google Scholar 

  28. Meher, P. K. (2005). Design of a fully-pipelined systolic array for flexible transposition-free VLSI of 2-D DFT. IEEE Transactions on Circuits and Systems. II: Express Briefs, 52(2), 85–89.

    Article  Google Scholar 

  29. Meher, P. K. (2006). Efficient systolic implementation of DFT using a low-complexity convolution-like formulation. IEEE Transactions on Circuits and Systems. II: Express Briefs, 53(8), 702–706.

    Article  MathSciNet  Google Scholar 

  30. Meher, P. K. (2006). Highly concurrent reduced-complexity 2-D systolic array for discrete Fourier transform. IEEE Signal Processing Letters, 13(8), 481–484.

    Article  Google Scholar 

  31. Meher, P. K., Patra, J. C., & Vinod, A. P. (2006). A 2-D systolic array for high-throughput computation of 2-D discrete fourier transform. In Proc. IEEE Asia-Pacific conerence on circuits and systems (APCCAS-06) (pp. 1929–1932), December.

  32. Meher, P. K., Patra, J. C., & Vinod, A. P. (2007). Novel recursive solution for area-time efficient systolization of discrete Fourier transform. In 2007 IEEE International Symposium on Circuits and Systems, ISCAS ’07, May.

  33. Press, W., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. (1992). Numerical recipes in C: The art of scientific computing. Cambridge: Cambridge University Press.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Computer Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore, 639798, Singapore

    Pramod K. Meher, Jagdish C. Patra & A. P. Vinod

Authors
  1. Pramod K. Meher
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jagdish C. Patra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. P. Vinod
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pramod K. Meher.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Meher, P.K., Patra, J.C. & Vinod, A.P. Efficient Systolic Designs for 1- and 2-Dimensional DFT of General Transform-Lengths for High-Speed Wireless Communication Applications. J Sign Process Syst Sign Image Video Technol 60, 1–14 (2010). https://doi.org/10.1007/s11265-008-0328-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11265-008-0328-x

Keywords

Search

Navigation