Monaural Speech Separation Based on Gain Adapted Minimum Mean Square Error Estimation

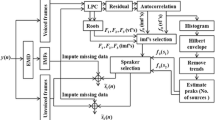
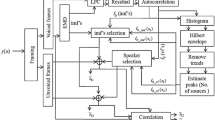
Abstract

We present a new model-based monaural speech separation technique for separating two speech signals from a single recording of their mixture. This work is an attempt to solve a fundamental limitation in current model-based monaural speech separation techniques in which it is assumed that the data used in the training and test phases of the separation model have the same energy level. To overcome this limitation, a gain adapted minimum mean square error estimator is derived which estimates sources under different signal-to-signal ratios. Specifically, the speakers’ gains are incorporated as unknown parameters into the separation model and then the estimator is derived in terms of the source distributions and the signal-to-signal ratio. Experimental results show that the proposed system improves the separation performance significantly when compared with a similar model without gain adaptation as well as a maximum likelihood estimator with gain estimation.

Appendices

Appendix A: Proof of (24)

In this appendix we show that $p(x_{1}(d)|{\mathbf y},\theta,k_1^r,k_2^r)$ is given by Eq. 24. Using Bayes’ theorem and the probability chain rule and noting that the sources are independent, we can express $p(x_1^r(d)|{\mathbf y},\theta,k_1^r,k_2^r)$ in terms of the observation probability and the prior probability of the sources. Thus, we have

$$\begin{array}{lll} p\left(x_1^r(d)|{\mathbf y},\theta,k_1^r,k_1^r,k_2^r\right)&=&\displaystyle\frac{p\left(x_1^r(d),{\mathbf y},\theta,k_1^r,k_2^r\right)}{p\left({\mathbf y},\theta,k_1^r,k_2^r\right)}\nonumber\\ &=&\displaystyle\frac{\int_{x_2^r(d)} p\left(x_1^r(d),x_2^r(d),{\mathbf y},\theta,k_1^r,k_2^r\right)\,dx_2(d)}{\int_{x_1^r(d)}\int_{x_2^r(d)} p\left(x_1^r(d),x_2^r(d),{\mathbf y},\theta,k_1^r,k_2^r\right)\,dx_2(d)dx_1(d)}\nonumber\\ &=&\frac{\int_{x_2^r(d)} p\left({\mathbf y}|x_1^r(d),x_2^r(d),\theta,k_1^r,k_2^r\right) } {\int_{x_1^r(d)}\int_{x_2^r(d)} p\left({\mathbf y}|x_1^r(d),x_2^r(d),\theta,k_1^r,k_2^r\right)}\times \frac{p\left(x_1^r(d)|k_1^r\right)p\left(x_2^r(d)|k_2^r\right)\,dx_2(d) }{p\left(x_1^r(d)|k_1^r\right)p\left(x_2^r(d)|k_2^r\right)\,dx_2(d)dx_1(d)} \end{array}$$

(27)

Substituting Eqs. 14 and 15 into Eq. 27, we obtain

$$ p\left(x_1^r(d)|{\mathbf y},k_1^r,k_2^r\right) =\frac{\int_{x_2^r(d)} \exp\left(\frac{-\left(y(d)-f\bigl(x^r_{1}(d),x^r_{2}(d),\theta\bigr)\right)^2}{2\sigma^2(d)}\right)}{\int_{x_1^r(d)} \int_{x_2^r(d)} \exp\left(\frac{-\left(y(d)-f\bigl(x^r_{1}(d),x^r_{2}(d),\theta\bigr)\right)^2}{2\sigma^2(d)}\right)} \times \frac{\exp\left(\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right) \exp\left(\frac{-\bigl(x_2^r(d)-\mu_2^{k_2^r}(d)\bigr)^2}{2\sigma_2^{2k_2^r}(d)}\right)\, dx_2(d)}{ \exp\left(\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right) \exp\left(\frac{-\bigl(x_2^r(d)-\mu_2^{k_2^r}(d)\bigr)^2}{2\sigma_2^{2k_2^r}(d)}\right)\,dx_2(d)dx_1(d)}. $$

(28)

In order to solve the integrations in Eq. 28 we consider the following conditions.

$$\begin{array}{lll} f\bigl(x^r_{1}(d),x^r_{2}(d),\theta\bigr)= \begin{cases} x_1(d)+h(\theta),& \mu^{k_1^r}_{1}(d)+h(\theta)\geq \mu^{k_2^r}_{2}(d)+h(-\theta)\qquad \text{condition}\, I\\[5pt] x_2(d)+h(-\theta),& \mu^{k_1^r}_{1}(d)+h(\theta)< \mu^{k_2^r}_{2}(d)+h(-\theta)\qquad \text{condition}\, II \end{cases}. \end{array}$$

(29)

Thus, under condition I, we have

$$ p\left(x_1^r(d)|{\mathbf y},k_1^r,k_2^r\right) =\frac{ \exp\left(\frac{-\bigl(y(d)-x_1^r(d)-h(\theta)\bigr)^2}{2\sigma^2(d)} +\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right)}{\int_{x_1^r(d)} \exp\left(\frac{-\bigl(y(d)-x_1^r(d)\bigr)^2}{2\sigma^2(d)}+ \frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right)dx_1(d)}. $$

(30)

The term in the $\exp(\cdot)$ function in Eq. 30 can be rewritten as

$$ -\frac{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}{2\sigma_1^{2k_1^r}(d)\sigma^2(d)} \times\left(x_1^r(d)-\frac{\sigma_1^{2k_1^r}(d)y(d)+\sigma_1^{2k_1^r}h(\theta)+\sigma^2(d)\mu_1^{k_1^r}(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}\right)^2 -\frac{\left(y(d)-h(\theta)-\mu_1^{k_1^r}(d)\right)^2}{2\left(\sigma_1^{2k_1^r}(d)+\sigma^2(d)\right)}. $$

(31)

Noting that the last term in Eq. 31 is independent of x ₁(d) and hence cancelled out, we GET

$$ p\left(x_1^r(d)|{\mathbf y},k_1^r,k_2^r\right) =\displaystyle \frac{\exp\left(-\frac{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}{2\sigma_1^{2k_1^r}(d)\sigma^2(d)}\bigg(x_1^r(d)-\frac{\sigma_1^{2k_1^r}(d)y(d)-\sigma_1^{2k_1^r}(d)h(\theta)+\sigma^2(d)\mu_1^{k_1^r}(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}\bigg)^2\right) }{\int_{x_1^r(d)}\exp\left(-\frac{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}{2\sigma_1^{2k_1^r}(d)\sigma^2(d)}\bigg(x_1^r(d)-\frac{\sigma_1^{2k_1^r}(d)y(d)-\sigma_1^{2k_1^r}(d)h(\theta)+\sigma^2(d)\mu_1^{k_1^r}(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}\bigg)^2\right)\,dx_1(d)}. $$

(32)

The integration in the denominator is simply calculated as

$$\begin{array}{lll} \int_{x_1^r(d)}\exp\left(-\frac{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}{2\sigma_1^{2k_1^r}(d)\sigma^2(d)}\left(x_1^r(d) -\frac{\sigma_1^{2k_1^r}(d)y-\sigma_1^{2k_1^r}(d)h(\theta)+\sigma^2(d)\mu_1^{k_1^r}(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}\right)^2\right)\,dx_1(d) \sqrt{2\pi \frac{\sigma_1^{2k_1^r}(d)\sigma^2(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}}. \end{array}$$

(33)

Substituting Eq. 33 into Eq. 32, we arrive at a Gaussian distribution in the form

$$\begin{array}{ll} p\left(x_1^r(d)|{\mathbf y},k_1^r,k_2^r\right)&= \frac{1}{\sqrt{2\pi \frac{\sigma_1^{2k_1^r}(d)\sigma^2(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}}} \exp\left(-\frac{\bigl(x_1^r(d)-\frac{\sigma_1^{2k_1^r}(d)y(d)-\sigma_1^{2k_1^r}(d)h(\theta)+\sigma^2(d)\mu_1^{k_1^r}(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}\bigr)^2} {2\frac{\sigma_1^{2k_1^r}(d)\sigma^2(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}}\right)\nonumber\\ &= \mathcal{N}\left(\frac{\sigma_1^{2k_1^r}(d)y(d)-\sigma_1^{2k_1^r}(d)h(\theta)+\sigma^2(d)\mu_1^{k_1^r}(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)},\frac{\sigma_1^{2k_1^r}(d)\sigma^2(d)}{\sigma_1^{2k_1^r}(d)+\sigma^2(d)}\right). \end{array}$$

(34)

In a similar fashion, under condition II Eq. 28 reduces to

$$\begin{aligned} & p\left(x_1^r(d)|{\mathbf y},k_1^r,k_2^r\right) \\ & \quad =\frac{ \int_{x_2^r(d)} \exp\left(\frac{-\bigl(y(d)-x_2^r(d)-h(-\theta)\bigr)^2}{2\sigma^2(d)}\right) \exp\left(\frac{-(x_2^r(d)-\mu_2^{k_2^r}(d))^2}{2\sigma_2^{2k_2^r}(d)}\right)\, dx_2(d)}{\int_{x_2^r(d)} \exp\left(\frac{-\bigl(y(d)-x_2^r(d)\bigr)^2}{2\sigma^2(d)}\right) \exp\left(\frac{-\bigl(x_2^r(d)-\mu_2^{k_2^r}(d)\bigr)^2}{2\sigma_2^{2k_2^r}(d)}\right)\,dx_2(d)}\times\frac{ \exp\left(\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right) }{ \int_{x_1^r(d)} \exp\left(\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right)\,dx_1(d)}\\ & \quad = \frac{\exp\left(\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right)}{\int_{x_1^r(d)} \exp\left(\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right)\,dx_1(d)}= \frac{1}{\sqrt{2\pi\sigma_1^{2k_1^r}(d)}}\exp\left(\frac{-\bigl(x_1^r(d)-\mu_1^{k_1^r}(d)\bigr)^2}{2\sigma_1^{2k_1^r}(d)}\right) =\mathcal{N}\left(\mu_{1d}^i,\sigma_1^{2k_1^r}(d)\right) \end{aligned}$$

(35)

Hence, Eqs. 34 and 35 give Eq. 23 in Section 3.

Appendix B: Quadratic Algorithm for Finding θ ^*

In this Appendix, the procedure for finding θ ^* given in Eq. 22 is described. The goal is to find a value at which the global maximum of Q(θ) occurs. Since Q(θ) is well-approximated by a convex function, a quadratic optimization approach can be used to find θ ^* with small numbers of iterations. (see Table 1 for the numerical results). Figure 10 shows a typical form of Q(θ) which eases the understanding of the algorithm presented in Table 2. Concisely speaking, the algorithm works as follows. First, the coordinates of three points of Q(θ) is determined, lets say {(θ _l ,A), (θ _c ,C),(θ _r ,B)}. Then, a quadratic function of the form f(x) = ax ² + bx + c is fitted to these three points and $x^*=-\frac{b}{2a}$ which maximizes f(x) is obtained in terms of {(θ _l ,A), (θ _c ,C),(θ _r ,B)} using a function called Quadratic(·), that is, $x^*=Quadratic(\theta_l,A,\theta_r,B,\theta_c,C)$. Next, using x ^* and Q(x ^*), the coordinates {(θ _l ,A), (θ _c ,C),(θ _r ,B)} are updated until a value of θ _c is reached such that Q(θ _l ) ≤ Q(θ _c ) ≥ Q(θ _r ).

Figure 10

Typical form of Q(θ) with three marked points corresponding to A = Q(θ _l ), C = Q(θ _c ), and B = Q(θ _r ).

Table 2 Quadratic optimization algorithm

Appendix C: Derivation of (10)

In this appendix, we show how the computation of the right-hand side of Eq. 9 leads to Eq. 10, that is

$$ E\Bigl(y^r(d)\big|x_1^r(d),x_2^r(d),\theta\Bigr) =\max\Bigl(x_1^r(d)+h(\theta),x_2^r(d)+h(-\theta)\Bigr). $$

(36)

The procedure is similar to that presented in [42] except that the source signal gains, g ₁ and g ₂, are incorporated. Let

$$ \begin{array}{ll} {\dot{{\mathbf x}}^r_i} & {=\Bigl|\mathcal{F}_D\Bigl(\{X_i(t)\}_{t=(r-1)M}^{(r-1)M+N-1}\Bigr)\Bigr|} \\ {} &{=\left[\dot{x}^r_i(0),\ldots,\dot{x}^r_i(d),\ldots,\dot{x}^r_i(D-1)\right]^{\top},} \end{array}$$

and

$$ \begin{array}{ll} \dot{{\mathbf y}}^r&=\Bigl|\mathcal{F}_D\Bigl(\{Y_i(t)\}_{t=(r-1)M}^{(r-1)M+N-1}\Bigr)\Bigr| \\ &=\left[\dot{y}^r(0),\ldots,\dot{y}^r(d),\ldots,\dot{y}^r(D-1)\right] \end{array}$$

represent the magnitudes of the D-point discrete Fourier transforms of sources and the observation signal, respectively. Let $\phi^r=\angle\mathcal{F}_{\!D}\Bigl(\!\{X_i(t)\}_{t=(r-1)M}^{(r-1)M+N-1}\!\Bigr)-$ $\angle\mathcal{F}_{\!D}\Bigl(\!\{X_i(t)\}_{t=(r-1)M}^{(r-1)M+N-1}\!\Bigr)\!=\![\phi^r(0),\ldots,\phi^r(d),\ldots, \phi^r(D\!-1)\!]^{\top}$ where $\angle$ denotes the phase operator. Given Eq. 2, the relation between the log magnitude of $\dot{y}^r_i(d)$ and those of $\dot{x}^r_i(d)$, i ∈ {1,2} is given by

$$ \begin{array}{ll} y^r(d)&=\log_{10}\dot{y}^r(d) \\ &=\frac{1}{2}\log_{10}\Bigl[ g_1^2\bigl(\dot{x}^r_1(d)\bigr)^2+g_2^2\bigl(\dot{x}^r_2(d)\bigr)^2 \\ & \qquad\qquad\, +2g_1g_2\dot{x}^r_1(d) \dot{x}^r_2(d)\cos\bigl(\mathrm{\phi}^r(d)\bigr)\Bigr]. \end{array}$$

(37)

The goal is to obtain the MMSE estimate of y ^r(d) given $x_1^r(d)$, $x_2^r(d)$, g ₁, and g ₂. Mathematically, the MMSE estimator is expressed as

$$ \hat{y}^r(d)=E\Bigl(y^r(d)\big|x_1^r(d),x_2^r(d),g_1,g_2\Bigr). $$

(38)

From Eq. 37 and initially assuming that $\dot{x}_1^r(d)$,$\dot{x}_2^r(d)$, g ₁, and g ₂ are given, the only random variable on the right-hand side of Eq. 37 is φ ^r(d) which, as shown in [42], can be modeled by a uniform distribution over the interval [ − π;π]; that is $p\bigl(\phi^r(d)\bigr)=\frac{1}{2\pi}$ where $p\bigl(\phi^r(d)\bigr)$ denotes the PDF of φ ^r(d). Therefore,

$$\begin{array}{lll} \hat{y}^r(d)&=&\frac{1}{\pi}\int_0^{\pi} \frac{1}{2}\log_{10}\, \Biggl[ g_1^2\bigl(\dot{x}^r_1(d)\bigr)^2+g_2^2\bigl(\dot{x}^r_2(d)\bigr)^2\nonumber\\ && +2g_1g_2\dot{x}^r_1(d) \dot{x}^r_2(d)\cos\bigl(\mathrm{\phi}^r(d)\bigr)\Biggr]d\phi^r(d). \end{array}$$

(39)

The above integration is computed using an integration table (e.g. [63, pp. 111]) and the result is

$$\begin{array}{rl} \hat{y}^r(d)&= \max \Bigl(\log_{10}\bigl( g_1\dot{x}_1^r(d)\bigr),\log_{10}\bigl(g_2\dot{x}_2^r(d)\bigr)\Bigr)\nonumber\\ d&=0,\ldots,D-1. \end{array}$$

(40)

Noting that log₁₀ g ₁ = h(θ), log₁₀ g ₂ = h( − θ), and $\log_{10}\bigl(\dot{x}_i^r(d)\bigr)\!=\!x_i^r(d)$, i ∈ {1,2}, Eq. 40 can be rewritten as

$$ \hat{y}^r(d)=\max \bigl(x_1^r(d)+h(\theta),x_2^r(d)+h(-\theta)\bigr) $$

(41)

which is identical to Eq. 10.