Abstract
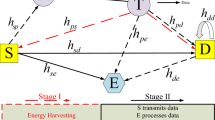
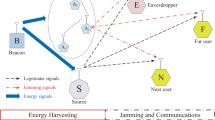
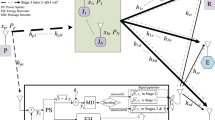
This paper proposes a jamming technique which employs a self-powered secondary jammer to interfere a wire-tapper, who eavesdrops communications between a self-powered secondary source and a secondary destination in energy harvesting cognitive radio networks (EHCRNs). For generality, interference from a primary source, maximum transmit power constraint and interference power constraint are considered in analyzing security performance of the proposed jamming technique in terms of security-reliability compromise. Towards this end, exact expressions of detection/eavesdropping outage probabilities at the destination/the wire-tapper are first proposed and then verified by computer simulations. Finally, results are provided to demonstrate the efficacy of the jamming technique and the key effects (interference from the primary user, power constraints, interference power distribution factor, and time splitting factor) on security performance of EHCRNs.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Zlatanov, N., Schober, R., & Hadzi-Velkov, Z. (2017). Asymptotically optimal power allocation for energy harvesting communication networks. IEEE Transactions on Vehicular Technology, 66(8), 7286–7301.
Ho-Van, K. (2017). On the performance of maximum ratio combining in cooperative cognitive networks with proactive relay selection under channel information errors. Telecommunication Systems, 65(3), 365–376.
Ho-Van, K. (2015). Outage analysis in cooperative cognitive networks with opportunistic relay selection under imperfect channel information. International Journal of Electronics and Communications, 69(11), 1700–1708.
Darsena, D., Gelli, G., & Verde, F. (2017). An opportunistic spectrum access scheme for multicarrier cognitive sensor networks. IEEE Sensors Journal, 17(8), 2596–2606.
FCC (2002). Spectrum policy task force report. ET Docket 02135, November 2002.
Liu, Y., Chen, H. H., & Wang, L. (2017). Physical layer security for next generation wireless networks: Theories, technologies, and challenges. IEEE Communications Surveys & Tutorials, 19(1), 347–376. First Quarter.
Hu, J., Cai, Y., Yang, N., Zhou, X., & Yang, W. (2017). Artificial-noise-aided secure transmission scheme with limited training and feedback overhead. IEEE Transactions on Wireless Communications, 16(1), 193–205.
Wang, C., & Wang, H. M. (2014). On the secrecy throughput maximization for MISO cognitive radio network in slow fading channels. IEEE Transactions on Information Forensics and Security, 9(11), 1814–1827.
Wang, D., Ren, P., Du, Q., Sun, L., & Wang, Y. (2016). Cooperative relaying and jamming for primary secure communication in cognitive two-way networks. In Proceedings of IEEE VTC, Nanjing, China, 15–18 May 2016 (pp. 1–5).
Fang, B., Qian, Z., Zhong, W., & Shao, W. (2015). AN-aided secrecy precoding for SWIPT in cognitive MIMO broadcast channels. IEEE Communications Letters, 19(9), 1632–1635.
Nguyen, V. D., Duong, T. Q., Dobre, O. A., & Shin, O. S. (2016). Joint information and jamming beamforming for secrecy rate maximization in cognitive radio networks. IEEE Transactions on Information Forensics and Security, 11(11), 2609–2623.
Fang, B., Qian, Z., Shao, W., & Zhong, W. (2016). Precoding and artificial noise design for cognitive MIMOME wiretap channels. IEEE Transactions on Vehicular Technology, 65(8), 6753–6758.
Wu, Y., Chen, X., & Chen, X. (2015). Secure beamforming for cognitive radio networks with artificial noise. In Proceedings of IEEE WCSP, Nanjing, China, 15–17 October 2015 (pp. 1–5).
Hu, X., Zhang, X., Huang, H., & Li, Y. (2016). Secure transmission via jamming in cognitive radio networks with possion spatially distributed eavesdroppers. In Proceedings of IEEE PIMRC, Valencia, Spain, 4–7 September 2016 (pp 1–6).
Cai, Y., Xu, X., & Yang, W. (2016). Secure transmission in the random cognitive radio networks with secrecy guard zone and artificial noise. IET Communications, 10(15), 1904–1913.
Nguyen, V. D., Duong, T. Q., Shin, O. S., Nallanathan, A., & Karagiannidis, G. K. (2017). Enhancing PHY security of cooperative cognitive radio multicast communications. IEEE Transactions on Cognitive Communications and Networking, 3(4), 599–613.
Quang, P. M., Duy, T. T., & Bao, V. N. Q. (2016). Performance evaluation of underlay cognitive radio networks over Nakagami-m fading channels with energy harvesting. In Proceedings of IEEE ATC, HaNoi, Vietnam, 10–12 October 2016 (pp. 108–113).
Zhang, J., Pan, G., & Wang, H. M. (2016). On physical-layer security in underlay cognitive radio networks with full-duplex wireless-powered secondary system. IEEE Access, 4, 3887–3893.
Mou, W., Yang, W., Xu, X., Li, X., & Cai, Y. (2016). Secure transmission in spectrum-sharing cognitive networks with wireless power transfer. In Proceedings of IEEE WCSP, JiangSu, China, 13–15 October 2016 (pp. 1–5).
Lei, H., Xu, M., Zhang, H., Pan, G., Ansari, I. S., & Qaraqe, K. A. (2016). Secrecy outage performance for underlay MIMO CRNs with energy harvesting and transmit antenna selection. In Proceedings of IEEE Globecom, Washington DC, USA, 4–8 December 2016 (pp. 1–6).
Singh, A., Bhatnagar, M. R., & Mallik, R. K. (2016). Secrecy outage of a simultaneous wireless information and power transfer cognitive radio system. IEEE Wireless Communications Letters, 5(3), 288–291.
Liu, Y., Wang, L., Zaidi, S. A. R., Elkashlan, M., & Duong, T. Q. (2016). Secure D2D communication in large-scale cognitive cellular networks: A wireless power transfer model. IEEE Transactions on Communications, 64(1), 329–342.
Raghuwanshi, S., Maji, P., Roy, S. D., & Kundu, S. (2016). Secrecy performance of a dual hop cognitive relay network with an energy harvesting relay. In Proceedings of IEEE ICACCI, Jaipur, India, 21–24 September 2016 (pp. 1622–1627).
Zhang, X., Xing, J., Yan, Z., Gao, Y., & Wang, W. (2013). Outage performance study of cognitive relay networks with imperfect channel knowledge. IEEE Communications Letters, 17(1), 27–30.
Seyfi, M., Muhaidat, S., & Liang, J. (2013). Relay selection in cognitive radio networks with interference constraints. IET Communications, 7(10), 922–930.
Ho-Van, K. (2017). Influence of channel information imperfection on outage probability of cooperative cognitive networks with partial relay selection. Wireless Personal Communications, 94(4), 3285–3302.
Zhihui, S., Yi, Q., & Song, C. (2013). On physical layer security for cognitive radio networks. IEEE Network, 27, 28–33.
Sharma, R., & Rawat, D. (2015). Advances on security threats and countermeasures for cognitive radio networks: A survey. IEEE Communications Surveys & Tutorials, 17(2), 1023–1043.
Li, Z., Jing, T., Cheng, X., Huo, Y., Zhou, W., & Chen, D. (2015) Cooperative jamming for secure communications in MIMO cooperative cognitive radio networks. In Proceedings of IEEE ICC, London, UK, 8–12 June 2015 (pp. 7609–7614).
Zou, Y. (2017). Physical-layer security for spectrum sharing systems. IEEE Transactions on Wireless Communications, 16(2), 1319–1329.
Liu, Y., Wang, L., Duy, T. T., Elkashlan, M., & Duong, T. Q. (2015). Relay selection for security enhancement in cognitive relay networks. IEEE Wireless Communications Letters, 4(1), 46–49.
Chakraborty, P., & Prakriya, S. (2017). Secrecy performance of an idle receiver assisted underlay secondary network. IEEE Transactions on Vehicular Technology, 66(10), 9555–9560.
Biglieri, E., Proakis, J., & Shamai, S. (1998). Fading channels: Information-theoretic and communications aspects. IEEE Transactions on Information Theory, 44(6), 2619–2692.
Gradshteyn, I. S., & Ryzhik, I. M. (2000). Table of integrals, series and products (6th ed.). San Diego, CA: Academic Press.
Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant number 102.04-2017.01
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Exact closed-form representations of special integrals
This appendix defines integrals whose exact closed forms are expressed as (34)–(43).
The first integral is
Applying the series expansion to \({e^{ - \frac{b}{z}}}\), one can rewrite (46) as
By defining the below integral
one easily represents (47) in an exact closed form as (34).
By using [34, eq. (358.4)], one also expresses (48) in an exact closed form as (43).
The next integral is
Applying the series expansion to \({e^{ - \frac{b}{z}}}\), one can rewrite (49) as
The second integral in (50) can be simplified by the partial fraction decomposition as
The integral
can be represented in an exact closed form as (38) with the help of [34, eq. (358.2)].
Using (48) and (52), one can represent (51) in an exact closed form as (35).
The integral
can be simplified by performing the variable change \(x=1/y\) as
Applying (52) for integrals in the last equality of (54), one can express \({\mathcal{J}_3}\left( {c,a,b} \right) \) in an exact closed form as (36).
The integral
can be represented through \({\mathcal{J}_3}\left( {c,a,b} \right) \) as
Using the exact closed form of \({\mathcal{J}_3}\left( {c,a,b} \right) \) in (36), one can express (56) as (37).
The integral
can be simplified by performing the variable change \(x=1/y\) as
Applying (52) for integrals in the last equality of (58), one can express \({\mathcal{J}_6}\left( {c,a,b} \right) \) in an exact closed form as (39).
The integral
can be simplified by applying the series expansion to \({{e^{ - \frac{b}{z}}}}\) as
Using (48) for the last integral in (60), one can represent (60) in an exact closed form as (40).
The integral
can be represented through \({\mathcal{J}_6}\left( {c,a,b} \right) \) as
Using the exact closed form of \({\mathcal{J}_6}\left( {c,a,b} \right) \) in (39), one can express (62) as (41).
The integral
can be simplified by applying the series expansion to \({{e^{ - \frac{b}{z}}}}\) as
Using (48) for the last integral in (64), one can represent (64) in an exact closed form as (42).
Appendix B: The pdfs of \(P_s\) and \(P_j\)
This appendix derives the pdfs of \(P_s\) in (19) and \(P_j\) in (20).
The cdf of \(P_s\) is defined as
Inserting (19) into (65), one can expand (65) as
Inserting (12) into (66) and averaging the result over \({{{\left| {{h_{ts}}} \right| }^2}}\), (66) is simplified as
It is recalled from the definition of the step function that \({\mathcal {U}\left( {x - \frac{{\alpha {\eta _s}}}{{1 - \alpha }}\left[ {{P_t}y + \sigma _s^2} \right] } \right) }\) equals 1 when \(\frac{{\left( {1 - \alpha } \right) x}}{{\alpha {\eta _s}{P_t}}} - \frac{{\sigma _s^2}}{{{P_t}}} \ge y\). Also, \(y = {\left| {{h_{ts}}} \right| ^2}\ge 0\) and hence, \({\mathcal {U}\left( {x - \frac{{\alpha {\eta _s}}}{{1 - \alpha }}\left[ {{P_t}y + \sigma _s^2} \right] } \right) }\)\(=1\) when \(\frac{{\left( {1 - \alpha } \right) x}}{{\alpha {\eta _s}{P_t}}} - \frac{{\sigma _s^2}}{{{P_t}}} \ge y\) and \(x \ge \frac{{\alpha {\eta _s}\sigma _s^2}}{{1 - \alpha }}\). Using this fact in (67), one can simplify it as
The last integral in (68) makes the expression of \({F_{{P_s}}}\left( x \right) \) complicated. However, various results in Sect. 4 illustrate that its effect is negligible. Therefore, after ignoring it and using notations (\(L_s\), \(M_s\), \(N_s\)) in (23), (24), (25), one can rewrite (68) in a compact form as
Taking the derivative of \({F_{{P_s}}}\left( x \right) \) with respect to x, one obtains the pdf of \(P_s\) as
Similarly, the pdf of \(P_j\) can be expressed as
where \(L_j\), \(M_j\), and \(N_j\) are defined in (28), (29), and (30), respectively.
Appendix C: Proof of theorem 1
Inserting (7) into (21) and after some manipulations, one obtains
Using (1) for \({{F_{{{\left| {{h_{sd}}} \right| }^2}}}\left( {\frac{{{\gamma _0}}}{{{P_s}}}\left[ {{P_t}{{\left| {{h_{td}}} \right| }^2} + \sigma _d^2} \right] } \right) }\), (72) is further simplified as
where
with \(A_d\) and \(B_d\) defined in (26) and (27), respectively.
Using the definition of the statistical average, (74) is rewritten as
Inserting (70) into (75) and after some manipulations, one obtains
Performing the partial fraction decomposition, (76) is further simplified as
Expressing the integrals in (77) in terms of special functions in (46), (49), (53), (55), (63), one can reduce (77) to
Inserting (78) into (73), one reduces (73) to (44), completing the proof.
Appendix D: Proof of theorem 2
Inserting (8) into (22) and after some manipulations, one obtains
where
and \(B_w\) is given by (33).
The \({\varPsi _t}\) term can be expressed in an exact closed form as
where \(A_w\) is given by (32).
Similarly, the \({\varPsi _j}\) term can be expressed in an exact closed form as
where C is given by (31).
Inserting (82) and (83) into (79), one can rewrite (79) as
Inserting (71) into the \(\varPhi \left( {{P_s}} \right) \) term in (84), one can represent \(\varPhi \left( {{P_s}} \right) \) as
Applying the partial fraction decomposition, \(\varUpsilon \) is rewritten as
Inserting (86) into (85) and using the definitions of the integrals in (49), (52), (57), (59), (61), (63), one can express \({\varPhi \left( {{P_s}} \right) }\) in an exact closed form as
Inserting (87) and (70) into (84), one obtains (45), completing the proof.
Rights and permissions
About this article
Cite this article
Ho-Van, K., Do-Dac, T. Performance analysis of jamming technique in energy harvesting cognitive radio networks. Telecommun Syst 70, 321–336 (2019). https://doi.org/10.1007/s11235-018-0477-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11235-018-0477-6