Abstract
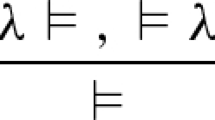
There are still on-going debates on what exactly is wrong with Prior’s pathological “tonk.” In this article I argue, on the basis of categorical inferentialism, that (i) two notions of inconsistency ought to be distinguished in an appropriate account of tonk; (ii) logic with tonk is inconsistent as the theory of propositions, and it is due to the fallacy of equivocation; (iii) in contrast to this diagnosis of the Prior’s tonk problem, nothing is actually wrong with tonk if logic is viewed as the theory of proofs rather than propositions, and tonk perfectly makes sense in terms of the identity of proofs. Indeed, there is fully complete semantics of proofs for tonk, which allows us to link the Prior’s old philosophical idea with contemporary issues at the interface of categorical logic, computer science, and quantum physics, and thereby to expose commonalities between the laws of Reason and the laws of Nature, which are what logic and physics are respectively about. I conclude the article by articulating the ideas of categorical logical positivism and pluralistic unified science as its goal, including the unification of realist and antirealist conceptions of meaning by virtue of the categorical logical basis of metaphysics.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Abramsky, S., & Coecke, B. (2008). Categorical quantum mechanics. In K. Engesser, D. M. Gabbay, & D. Lehmann (Eds.), Handbook of quantum logic and quantum structures (pp. 261–324). Amsterdam: Elsevier.
Abramsky, S., & Tzevelekos, N. (2011). Introduction to categories and categorical logic. In B. Coecke (Ed.), New structures for physics (pp. 3–94). Springer.
Belnap, N. (1962). Tonk, plonk and plink. Analysis, 22, 130–134.
Brandom, R. (2000). Articulating reasons: An introduction to inferentialism. Cambridge: HUP.
Cook, R. T. (2005). What’s wrong with tonk (?). The Journal of Philosophical Logic, 34, 217–226.
Dummett, M. (1991). The logical basis of metaphysics. Cambridge: Harvard University Press.
Friedman, M. (2000). A parting of the ways. Peru: Open Court Publishing.
Girard, J.-Y. (1995). Linear logic. In J.-Y. Girard, Y. Lafont, & L. Regnier (Eds.), Advances in linear logic. London: CUP.
Girard, J.-Y., Lafont, Y., & Taylor, P. (1989). Proofs and types. Cambridge: CUP.
Ladyman, J. (2014). Structural realism. In E. N. Zalta, (Ed.), Stanford encyclopedia of philosophy. Stanford: Stanford University.
Lambek, J., & Scott, P. (1986). Introduction to higher-order categorical logic. Cambridge: CUP.
Lawvere, F. W. (1969). Adjointness in foundations. Dialectica, 23, 281–296.
Maruyama, Y. (forthcoming). Categorical harmony and paradoxes in proof-theoretic semantics. In P. Schroeder-Heister, & T. Piecha (Eds.), Advances in proof theoretic semantics. Trends in logic. Berlin: Springer. http://www.springer.com/us/book/9783319226859.
Miller, A. (2014). Realism. In E. N. Zalta (Ed.), Stanford encyclopedia of philosophy. Stanford: Stanford University.
Priest, G. (2002). Paraconsistent logic. In D. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic (Vol. 6, pp. 287–393). Oxford: Oxford University Press.
Prior, A. N. (1960). The Runabout inference-ticket. Analysis, 21, 38–39.
Schroeder-Heister, P. (2012). Proof-theoretic semantics, self-contradiction, and the format of deductive reasoning. Topoi, 31, 77–85.
Zucker, J. (1974). The Correspondence between cut-elimination and normalization. Annals of Mathematical Logic, 7, 1–112.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Maruyama, Y. Prior’s tonk, notions of logic, and levels of inconsistency: vindicating the pluralistic unity of science in the light of categorical logical positivism. Synthese 193, 3483–3495 (2016). https://doi.org/10.1007/s11229-015-0932-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0932-9