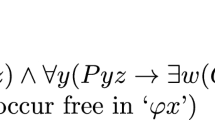Abstract
Say that mereological harmony is the view that there is at least some mirroring between the mereological structure of material objects and the mereological structure of their locations: each, in some way, mirrors the other. As it turns out, there is a confusing array of systems of harmony available to the substantivalist. In this paper, I attempt to bring some order to these systems. I explore some systems found in the literature, as well as some natural systems which haven’t been discussed. Along the way, I explore a number of metaphysical consequences of the different systems of harmony. The paper ends with a roadmap of possible views for the substantivalist.
Similar content being viewed by others
Notes
This exotic possibility is defended in Saucedo (2011).
Or, perhaps, spatial regions really exist. While I’ll proceed by assuming that eternalism is true, everything I say about spacetime regions can be interpreted in a presentist-friendly way.
For simplicity, I assume that the parthood relation is a dyadic relation. Those who think that parthood is either a three-place or four-place relation might want to characterize parthood misalignment cases differently. For instance, if parthood is a three-place relation holding among two objects and a time, then a parthood misalignment case might be characterized as x being a part of y at time t without x’s location being a part of y’s location at t, or vice versa. Though there are many interesting ways in which conceptions of parthood as a three- or four-place relation relate to mereological harmony, this exploration would take us too far outside the scope of the current paper.
There are a number of ways of axiomatizing (CM). Let’s follow Hovda (2008) and say that t is a fusion of a set s in accordance with the following definition:
$$\begin{aligned} Fu(t, s) =_{df} \forall x(x \in s \rightarrow x \le t) \wedge \forall y(y \le t \rightarrow \exists x (x \in s \wedge y \circ x)) \end{aligned}$$This is what Hovda calls a type-2 fusion. (CM) can now be axiomatized in the following way:
-
(1)
\((x \le y \wedge y \le z ) \rightarrow x \le z\)
-
(2)
\(\exists x \varphi _x \rightarrow \exists !z Fu(z, \varphi _x)\)
-
(1)
As Parsons (2007) notes, an object o is weakly located at a region r iff r is not completely free of o.
And hence deny that locations are the sorts of things which are located at themselves. Thus, we deny Casati and Varzi (1999)’s principle of Conditional Reflexivity, the principle which says that: if x is located at y, then y is located at y.
Even though I make these assumptions for simplicity of presentation, I want to acknowledge that there are a number of reasons some might find the assumptions worrisome. First, one might think that multilocation is possible. Second, one might think that some objects fail to have exact locations. Suppose there are weird hybrid objects like the fusion of my left hand and \(\pi \). Where is this object located? Though some might claim that it is located exactly where my left hand is located, others might claim that it is only weakly located there, and it isn’t exactly located anywhere. There are plenty of similar cases. For instance, suppose that space is gunky and that there is a point-sized object o. While o might be weakly located in a number of regions, it might not have an exact location. Or suppose that space is knuggy, i.e., every region has a proper superregion, and that an object t completely fills in every region. While t is weakly located everywhere, it doesn’t seem to have an exact location. A total function f requires that the fusion “my left hand + \(\pi \)”, o, and t all have exact locations. I take these examples from Parsons (2007). Another case noted in Parsons (2007) and Nolan (2006), which was first shown by Shieva Kleinschmidt to have consequences for the thesis that everything with a weak location has an exact location, is the case of stoic gunk, though see Leonard (2014) for why this case is a bit more complicated than the three examples mentioned above.
As Uzquiano notes, every proper part is a proper proper part in (CM).
Uzquiano (2011) includes a number of relevant countermodels. See pp. 204–210.
That is: \(x\le y =_{df} yFu\lbrace x,y \rbrace \)
It’s worth noting that she relativizes the parthood relation to times. But all of the systems I consider can also be relativized to times or, say, regions of spacetime for those dualists who reject the notion that parthood is a 2-place relation.
The formulation there, however, distinguishes between parthood on regions and a relation of subregionhood.
But note that Saucedo (2011) just considers the system. He doesn’t endorse it. As mentioned above, he argues that all misalignment cases are possible.
It’s also worth noting that this system is slightly redundant. For example, Simplicity is equivalent to Complexity.
In other words, the following model \({\mathcal {M}} = \lbrace D, I \rbrace \):
\({\mathcal {D}} = \lbrace a_1, r_1, r_2, r_3, \ldots \rbrace \)
\(\mathcal {I(\le )} = \lbrace \langle a, a \rangle , \ldots , \langle r_2, r_1 \rangle , \langle r_3, r_1 \rangle , \langle r_4, r_2 \rangle , \langle r_5, r_2 \rangle , \langle r_6, r_3 \rangle , \langle r_7, r_3 \rangle , \ldots \rbrace \)
\({\mathcal {I}}(f) = \lbrace \langle a_1, r_1 \rangle \rbrace \)
Of course, this relies on the assumption that spacetime atoms are themselves unextended entities. See Braddon-Mitchell and Miller (2006) for a defense of why this might not be the case. Thanks to an anonymous referee for pointing this out.
It’s important to note that only mereological sentences are substitutable. For instance, predicates like ‘is a material object’ or ‘ is a region’ are not substitutable for ‘\(\varphi \)’ because they are not expressible in mereology. Otherwise, they’d clearly hold of some material objects, or regions, though not vice versa. Also, names are banned. So when ‘r’ is a name, ‘\(r \le x\)’ is not substitutable for ‘\(\varphi x\)’. Thanks to Ted Sider for noting this point about names.
Note that the identity relation appears in the definiens of (has exactly n parts), so (Number of Parts) isn’t an instance of MH \(_4-\). Nonetheless, (No Numerical Difference) is guaranteed by MH \(_4-\), as objects with different numbers of parts can be distinguished purely in terms of mereology without identity.
Thanks to Aldo Antonelli for first bringing to my attention Identity. I should make two brief remarks concerning (No Co-location). First, in the setup of the paper, we noted that we weren’t going to take locations to be located at themselves. If we had, then we would have run into some additional trouble with MH \(_4+\). In particular, this system of harmony is inconsistent with (the dualist idea) that my body and my location are co-located and yet distinct. Second, one of the responses to the expansions problem for the universalist was to admit of cross-categorial fusions. It’s worth noting that if one takes this route, and one also thinks that such entities are located entities, then MH \(_4+\) causes some trouble. In particular, my body and the fusion of my body and my location are co-located, yet distinct. One, however, could naturally say that cross-categorial fusions of this sort simply lack exact locations.
It is worth noting, however, that Markosian (2014) also seems to accept something like MH \(_{1\le }\) when he proposes his subregion theory of parthood. So it looks like the view in Markosian (2014) is a conjunction of MH \(_{1\le }\) and Object Mirroring, though none of this is explicitly spelled out in the paper.
This is assumed, at least with respect to parthood, in Jansen and Schulz (2014), though the location relation they use is, as they admit, slightly broader than the location relation typically discussed and the notion I assume in this paper.
Thanks to Gabriel Uzquiano for originally pointing this out to me.
See Shiver (2015) for a discussion on how to formulate the claim that “everything is ultimately composed of atoms.”
In the preliminary section of this paper, I assumed that the parthood relation on material objects is the same parthood relation on regions of spacetime. This is something which the view Nolan develops rejects; however, a host-version of the expansions generating instance of harmony with the caveat that parthood is a relation on material objects and subregionhood is a relation on regions, is compatible with Nolanian supersubstantivalism; and the unrestricted full-blown instance is not.
Though we didn’t show that the left-to-right direction of MH \(_{1\le }\) is equivalent to the left-to-right direction of HH \(^-\), this proof can be read off of the inductive proof above for the thesis that MH \(_{1\le }\) entails HH \(^-\).
For instance, though MH \(_4+\) has every principle in parentheses as a consequence, MH \(_{1\circ }\) only has the two consequences written underneath in.
References
Braddon-Mitchell, D., & Miller, K. (2006). The physics of extended simples. Analysis, 66(3), 222–226.
Casati, R., & Varzi, A. (1999). Parts and places: The structures of spatial representation. Cambridge: MIT Press.
Donnelly, M. (2010). Parthood and multi-location. In D. Zimmerman (Ed.), Oxford studies in metaphysics (5th ed.). Oxford: Oxford University Press.
Gilmore, C. (2006). Where in the relativistic world are we? In J. Hawthorne (Ed.), Philosophical perspectives, Vol. 20: Metaphysics. Oxford: Blackwell.
Hawthorne, J. (2008). Three-dimensionalism vs. four-dimensionalism. In T. Sider, J. Hawthorne, & D. Zimmerman (Eds.), Contemporary debates in metaphysics (pp. 263–282). Oxford: Blackwell.
Hovda, P. (2008). What is classical mereology? Journal of Philosophical Logic, 38(1), 55–82.
Hudson, H. (2001). A materialist metaphysics of the human person. Ithaca, NY: Cornell University Press.
Jansen, L., & Schulz, S. (2014). Crisp islands in vague seas: Cases of determinate parthood relations in biological objects. In C. Calosi & P. Graziani (Eds.), Mereology and the sciences (pp. 165–190). Berlin: Springer.
Leonard, M. (2014). Locating gunky water and wine. Ratio, 27(3), 306–315.
Markosian, N. (1998). Simples. Australasian Journal of Philosophy, 76(2), 213–228.
Markosian, N. (2014). A spatial approach to mereology. In S. Kleinschmidt (Ed.), Mereology and location. Oxford: Oxford University Press.
McDaniel, K. (2006). Gunky objects in a simple world. Philo, 9(1), 39–46.
McDaniel, K. (2007). Extended simples. Philosophical Studies, 133(1), 131–141.
Nolan, D. (2006). Stoic gunk. Phronesis, 51(2), 162–183.
Nolan, D. (2014). Balls and all. In S. Kleinschmidt (Ed.), Mereology and location (pp. 91–116). Oxford: Oxford University Press.
Parsons, J. (2000). Must a four-dimensionalist believe in temporal parts? The Monist, 83(3), 399–418.
Parsons, J. (2007). Theories of location. In D. Zimmerman (Ed.), Oxford studies in metaphysics (Vol. 3, pp. 201–232). Oxford: Oxford University Press.
Sattig, T. (2006). The language and reality of time. Oxford: Clarendon Press.
Saucedo, R. (2011). Parthood and location. In D. Zimmerman (Ed.), Oxford studies in metaphysics (Vol. 6). Oxford: Oxford University Press.
Schaffer, J. (2009). Spacetime the one substance. Philosophical Studies, 145, 131–148.
Shiver, A. (2015). How do you say ‘everything is ultimately composed of atoms’? Philosophical Studies, 172(3), 607–614.
Sider, T. (2001). Four-dimensionalism: An ontology of persistence and time. Oxford: Oxford University Press.
Simons, P. (1987). Parts: A study in ontology. Oxford: Oxford University Press.
Skow, B. (2005). Once upon a spacetime. Ph.D. Thesis, New York University.
Thomson, J. J. (1998). The statue and the clay. Nous, 32(2), 149–173.
Uzquiano, G. (2011). Mereological harmony. In D. Zimmerman (Ed.), Oxford studies in metaphysics (Vol. 6, pp. 199–224). Oxford: Oxford University Press.
Varzi, A. (2007). Spatial reasoning and ontology: Parts, wholes, and locations. In M. Aiello, I. E. Pratt-Hartmann, & J. F. A. K. van Benthem (Eds.), Handbook of spatial logics (pp. 945–1038). Berlin: Springer.
Acknowledgments
For helpful comments and discussion on earlier drafts of this paper (some drafts being quite distant in the past), I’d like to thank Aldo Antonelli, Andrew Bacon, Mark Balaguer, Jacek Brzozowski, Tim Crane, Scott Dixon, Maegan Fairchild, Kit Fine, Thomas Hall, Daniel Korman, David Kovacs, Bernard Molyneux, Josh Parsons, Ben Rhors, Raul Saucedo, Jonathan Schaffer, Adam Sennet, Ted Shear, Anthony Shiver, Ted Sider, Robert Stalnaker, Michael Tooley, Jim Van Cleve, Emanuel Viebahn, Andy Yu, Alexander Zambrano, audiences at Oxford University, Yale University, Stanford University, Colorado (Boulder), UC Davis, Western Washington University, the University of Cologne, the University of Belgrade, and the 2013 Pacific APA. Special thanks to Cody Gilmore, John Hawthorne, Shieva Kleinschmidt, Jeff Russell, Gabriel Uzquiano and two anonymous referees for extensive comments on multiple drafts of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Leonard, M. What is mereological harmony?. Synthese 193, 1949–1965 (2016). https://doi.org/10.1007/s11229-015-0822-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0822-1