Reliability analysis of complete cubic networks based on extra conditional fault

Abstract

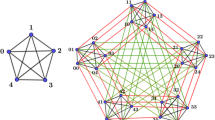
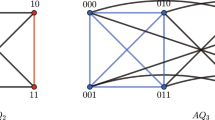
The reliability of multiprocessor systems is now a crucial concern in parallel computing, which can be characterized as connectivity and diagnosability. The s-extra connectivity (s-EC) $\kappa _s(G)$ of a network G is the minimum number of nodes whose deletion disconnects the network G, and every remaining component has no less than $s+1$ nodes. The s-extra diagnosability (s-ED) $t_s(G)$ of a network G is the maximum cardinality of faulty nodes that can be identified, given that each remaining component has at least $s+1$ nodes. This paper investigates the s-EC and s-ED of the complete cubic network CCN(n). Specifically, we initially demonstrate that the s-EC of CCN(n) is $\kappa _s(CCN(n))=(s+1)(n+1)-\frac{s(s+3)}{2}$ for $n\ge 3$ and $0\le s\le n-2$. Subsequently, we demonstrate that the s-ED under the PMC model is $t_s(CCN(n))=(s+1)(n+1)-\frac{s(s+3)}{2}+s$ for $n\ge 3$ and $1\le s\le n-2$. Similarly, under the MM* model, the s-ED is $t_s(CCN(n))=(s+1)(n+1)-\frac{s(s+3)}{2}+s$ for $n\ge 6$ and $1\le s\le \frac{n-2}{4}$. Finally, we conduct simulation experiments, and the results indicate that the s-EC consistently surpasses other known connectivities, including classical connectivity and s-component connectivity. Additionally, the s-ED consistently outperforms classical diagnosability and s-component diagnosability of CCN(n).