Analysis of a discrete-time two-class randomly alternating service model with Bernoulli arrivals | Queueing Systems Skip to main content
Springer Nature Link
Log in

Analysis of a discrete-time two-class randomly alternating service model with Bernoulli arrivals

  • Published:
Queueing Systems Aims and scope Submit manuscript

Abstract

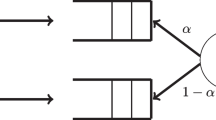
We analyze a discrete-time two-class queueing system with a single server which is alternately available for only one customer class. The server is each time allocated to a customer class for a geometrically distributed amount of time. Service times of the customers are deterministically equal to 1 time slot each. During each time slot, both classes can have at most one arrival. The bivariate process of the number of customers of both classes can be considered as a two-dimensional nearest-neighbor random walk. The generating function of this random walk has to be obtained from a functional equation. This type of functional equation is known to be difficult to solve. In this paper, we obtain closed-form expressions for the joint probability distribution for the number of customers of both classes, in steady state.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. We remark that \(\Delta (z)=-\sqrt{D_Y(z)}\) if \(z\in [1,\tau _T]\), due to the properties of the principal square root.

References

  1. Adan, I.J.B.F., Wessels, J., Zijm, W.H.M.: A compensation approach for two-dimensional Markov processes. Adv. Appl. Probab. 25(4), 783–817 (1993)

    Article  Google Scholar 

  2. Adan, I.J., Boxma, O.J., Resing, J.A.C.: Queueing models with multiple waiting lines. Queueing Syst. 37(1–3), 65–98 (2001)

    Article  Google Scholar 

  3. Bruneel, H., Kim, B.G.: Discrete-Time Models for Communication Systems Including ATM, vol. 205. Springer, Berlin (2012)

    Google Scholar 

  4. Cohen, J.W., Boxma, O.J.: Boundary Value Problems in Queueing System Analysis. North-Holland, Amsterdam (1983)

    Google Scholar 

  5. Cohen, J.W.: On the Determination of the Stationary Distribution of a Symmetric Clocked Buffered Switch. Teletraffic Science and Engineering, vol. 2, pp. 297–307. Elsevier, Amsterdam (1997)

    Google Scholar 

  6. Cohen, J.W.: On the asymmetric clocked buffered switch. Queueing Syst. 30(3–4), 385–404 (1998)

    Article  Google Scholar 

  7. Devos, A., Fiems, D., Walraevens, J., Bruneel, H.: An approximate analysis of a Bernoulli alternating service model. In: Phung-Duc, T., Kasahara, S., Wittevrongel, S. (eds.) Queueing Theory and Network Applications. QTNA 2019. Lecture Notes in Computer Science, vol. 11688. Springer, Cham (2019)

    Google Scholar 

  8. Fiems, D., Steyaert, B., Bruneel, H.: Randomly interrupted GI-G-1 queues: service strategies and stability issues. Ann. Oper. Res. 112(1–4), 171–183 (2002)

    Article  Google Scholar 

  9. Fiems, D., Maertens, T., Bruneel, H.: Queueing systems with different types of server interruptions. Eur. J. Oper. Res. 188(3), 838–845 (2008)

    Article  Google Scholar 

  10. Fayolle, G., Iasnogorodski, R.: Two coupled processors: the reduction to a Riemann–Hilbert problem. Z. Wahrscheinlichkeitstheorie verwandte Gebiete 47(3), 325–351 (1979)

    Article  Google Scholar 

  11. Fayolle, G., Malyshev, V.A., Iasnogorodski, R.: Random Walks in the Quarter-Plane. Springer, Berlin (1999)

    Book  Google Scholar 

  12. Kingman, J.F.: Two similar queues in parallel. Ann. Math. Stat. 32(4), 1314–1323 (1961)

    Article  Google Scholar 

  13. LaMaire, R.O.: An M/G/1 vacation model of an FDDI station. IEEE J. Sel. Areas Commun. 9(2), 257–264 (1991)

    Article  Google Scholar 

  14. Malyshev, V.A.: An analytical method in the theory of two-dimensional positive random walks. Sib. Math. J. 13(6), 917–929 (1972)

    Article  Google Scholar 

  15. Núñez-Queija, R.: Sojourn times in a processor sharing queue with service interruptions. Queueing Syst. 34(1–4), 351–386 (2000)

    Article  Google Scholar 

  16. Takagi, H.: Queueing Analysis: A Foundation of Performance Evaluation Volume 1: Vacation and Priority Systems, Part 1. North-Holland, Amsterdam (1991)

    Google Scholar 

  17. Takagi, H.: Queuing analysis of polling models. ACM Comput. Surv. (CSUR) 20, 5–28 (1998)

    Article  Google Scholar 

  18. Vanlerberghe, J., Maertens, T., Walraevens, J., De Vuyst, S., Bruneel, H.: On the optimization of two-class work-conserving parameterized scheduling policies. 4OR-Q J. Oper. Res. 14, 281–308 (2016)

    Article  Google Scholar 

  19. Walraevens, J., Steyaert, B., Bruneel, H.: Performance analysis of a single-server ATM queue with a priority scheduling. Comput. Oper. Res. 30(12), 1807–1829 (2003)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Telecommunications and Information Processing, Ghent University, Sint-Pietersnieuwstraat 41, 9000, Ghent, Belgium

    Arnaud Devos, Joris Walraevens, Dieter Fiems & Herwig Bruneel

Authors
  1. Arnaud Devos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Joris Walraevens
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dieter Fiems
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Herwig Bruneel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Arnaud Devos.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Devos, A., Walraevens, J., Fiems, D. et al. Analysis of a discrete-time two-class randomly alternating service model with Bernoulli arrivals. Queueing Syst 96, 133–152 (2020). https://doi.org/10.1007/s11134-020-09663-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11134-020-09663-x

Keywords

Mathematics Subject Classification

Search

Navigation