Abstract
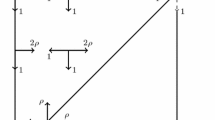
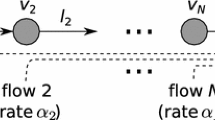
This paper investigates stability behavior in a variant of a generalized Jackson queueing network. In our network, some customers use a join-the-shortest-queue policy when entering the network or moving to the next station. Furthermore, we allow interarrival and service times to have general distributions. For networks with two stations we derive necessary and sufficient conditions for positive Harris recurrence of the network process. These conditions involve only the mean values of the network primitives. We also provide counterexamples showing that more information on distributions and tie-breaking probabilities is needed for networks with more than two stations, in order to characterize the stability of such systems. However, if the routing probabilities in the network satisfy a certain homogeneity condition, then we show that the stability behavior can be explicitly determined, again using the mean value parameters of the network. A byproduct of our analysis is a new method for using the fluid model of a queueing network to show non-positive recurrence of a process. In previous work, the fluid model was only used to show either positive Harris recurrence or transience of a network process.
Similar content being viewed by others
References
Bramson, M.: Stability of two families of queueing networks and a discussion of fluid limits. Queueing Syst. Theory Appl. 28, 7–31 (1998)
Dai, J.G.: On positive Harris recurrence of multiclass queueing networks: a unified approach via fluid limit models. Ann. Appl. Probab. 5, 49–77 (1995)
Dai, J.G.: A fluid-limit model criterion for instability of multiclass queueing networks. Ann. Appl. Probab. 6, 751–757 (1996)
Dai, J.G.: Stability of fluid and stochastic processing networks. In: MaPhySto Miscellanea Publication, No. 9, Centre for Mathematical Physics and Stochastics (1999)
Dai, J.G., Lin, W.: Maximum pressure policies in stochastic processing networks. Oper. Res. 53, 197–218 (2005)
Foley, R.D., McDonald, D.R.: Bridges and networks: exact asymptotics. Ann. Appl. Probab. 15, 542–586 (2005)
Foley, R.D., McDonald, D.R.: Large deviations of a modified Jackson network: stability and rough asymptotics. Ann. Appl. Probab. 15, 519–541 (2005)
Foss, S.G., Chernova, N.: On the stability of a partially accessible multi-station queue with state-dependent routing. Queueing Syst. Theory Appl. 29, 55–73 (1998)
Jackson, J.R.: Networks of waiting lines. Oper. Res. 5, 518–521 (1957)
Jackson, J.R.: Jobshop-like queueing systems. Manag. Sci. 10, 131–142 (1963)
Kurkova, I.A.: A load-balanced network with two servers. Queueing Syst. Theory Appl. 37, 379–389 (2001)
Medhi, J.: Stochastic Models in Queueing Theory, 2nd edn. Academic, San Diego (2002)
Resnick, S.I.: Adventures in Stochastic Processes. Birkhäuser, Boston (1992)
Suhov, Y.M., Vvedenskaya, N.D.: Fast Jackson networks with dynamic routing. Probl. Inf. Transm. 38, 136–153 (2002)
Wolff, R.W.: Stochastic Modeling and the Theory of Queues. Prentice Hall, Englewood Cliffs (1989)
Author information
Authors and Affiliations
Corresponding author
Additional information
J.G. Dai’s research supported in part by National Science Foundation grants DMI-0300599, CMMI-0727400 and CNS-0718701, and by an IBM Faculty Award.
J.J. Hasenbein’s research supported in part by National Science Foundation grant DMI-0132038.
B. Kim’s research was supported by the MIC (Ministry of Information and Communication), Korea, under the ITRC (Information Technology Research Center) support program supervised by the IITA (Institute of Information Technology Assessment).
Rights and permissions
About this article
Cite this article
Dai, J.G., Hasenbein, J.J. & Kim, B. Stability of join-the-shortest-queue networks. Queueing Syst 57, 129–145 (2007). https://doi.org/10.1007/s11134-007-9046-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-007-9046-5