Provably secure arbitrated-quantum signature

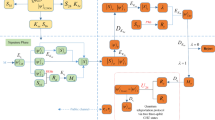
Abstract

Although the researchers have proposed many arbitrator quantum signature (AQS) for various applications in practice, the security proof of most AQSs was not strictly presented. Many results have shown that the AQS schemes without strict security proof may be broken by various measurement and forgery attacks. Therefore, a secure AQS should strictly put its security on the quantum theorems and principles. Based on the non-orthogonal entangled-triple sequence, an AQS with provable security is proposed. First, the theoretical security proof of our AQS is presented. Second, we prove the non-cloning theorem for the entangled-triple sequence. Third, by using the non-cloning property of the entangled-triple particle, we prove the new AQS signature cannot be forged. At last, the non-repudiation of the proposed AQS is analyzed. We showed that if an adversary can break the signature, his/her actions will violate some quantum principles. The security proof of the proposed signature scheme also shows the idea of provable security for a quantum signature. On the other hand, in the proposed scheme, the partners need not perform the probabilistic quantum state comparison test. It has better qubit efficiency. Therefore, compared with the other similar schemes, ours has the better merits in security and efficiency.

Appendices

Appendix A: A simple simulation of the proposed scheme

To simplify the example, we suppose the parameter n = 4. Assume that $f:\{ 0, \, 1\}^{*} \to \{ 0, \, 1\}^{4} \,$ is a public one-way hash function, and it has the uniform output.

1.1 Appendix A.1: Initializing phase

IS-1: By performing Bennett and Brassard’s BB84 Protocol, Trent and Alice share a random private key k. Assume k = (1001). Thus, k₁ = k₄ = 1, k₂ = k₃ = 0.

IS-2: Trent prepares four entangled-triple particles $\phi_{1}$, $\phi_{2}$, $\phi_{3}$ and $\phi_{4}$. The state of each particle $\phi_{i}$ (i = 1, 2, 3, 4) is $\left| {\phi_{i} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {0_{i}^{(T1)} 0_{i}^{(T2)} 0_{i}^{A} } \right\rangle \, + \left| {1_{i}^{(T1)} 1_{i}^{(T2)} 1_{i}^{A} } \right\rangle } \right)$. According to k, for each $\phi_{i}$(i = 1, 2, 3, 4), if k_i = 0, Trent performs the operator $I \otimes I \otimes I$ on $\phi_{i}$, or he performs the operator $H \otimes H \otimes H$ on $\phi_{i}$. Thus, the states of $\phi_{1}$, $\phi_{2}$, $\phi_{3}$ and $\phi_{4}$ are changed into

$$ \left\{ {\begin{array}{*{20}l} {\left| {\phi _{1} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{1}^{{(T1)}} + _{1}^{{(T2)}} + _{1}^{A} } \right\rangle + \left| { - _{1}^{{(T1)}} - _{1}^{{(T2)}} - _{1}^{A} } \right\rangle } \right)} \hfill \\ {\left| {\phi _{2} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{2}^{{(T1)}} 0_{2}^{{(T2)}} 0_{2}^{A} } \right\rangle {\text{ }} + \left| {1_{2}^{{(T1)}} 1_{2}^{{(T2)}} 1_{2}^{A} } \right\rangle {\text{ }}} \right)} \hfill \\ {\left| {\phi _{3} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{3}^{{(T1)}} 0_{3}^{{(T2)}} 0_{3}^{A} } \right\rangle {\text{ }} + \left| {1_{3}^{{(T1)}} 1_{3}^{{(T2)}} 1_{3}^{A} } \right\rangle {\text{ }}} \right)} \hfill \\ {\left| {\phi _{4} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{4}^{{(T1)}} + _{4}^{{(T2)}} + _{4}^{A} } \right\rangle + \left| { - _{4}^{{(T1)}} - _{4}^{{(T2)}} - _{4}^{A} } \right\rangle } \right)} \hfill \\ \end{array} } \right., $$

(A1)

where $\left| + \right\rangle = \left( {\left| 0 \right\rangle + \left| 1 \right\rangle } \right)/\sqrt 2$ and $\left| - \right\rangle = \left( {\left| 0 \right\rangle - \left| 1 \right\rangle } \right)/\sqrt 2$. According to $\phi_{1}$, $\phi_{2}$, $\phi_{3}$ and $\phi_{4}$, Trent composes three particle sequences $G_{T1} = \{ t_{1}^{(T1)} , \, t_{2}^{(T1)} ,t_{3}^{(T1)} , \, t_{4}^{(T1)} \}$, $G_{T2} = \{ t_{1}^{(T2)} , \, t_{2}^{(T2)} ,t_{3}^{(T2)} , \, t_{4}^{(T2)} \}$ and G_A = {a₁, a₂, a₃, a₄}, in which $t_{i}^{(T1)}$,$t_{i}^{(T2)}$, and a_i represent the 1st, the 2nd and the 3rd particle of $\phi_{i}$, respectively, where i = 1, 2, 3, 4.

IS-3: Trent randomly produces sufficient decoy particles whose states come from the non-orthogonal set $\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle ,\left| + \right\rangle ,\left| - \right\rangle } \right\}$. Then, Trent mixes them with G_A at random and gets the new non-orthogonal sequence $G^{\prime}_{A}$. After that, Trent transmits the sequence $G^{\prime}_{A}$ to Alice.

IS-4: After Alice receives $G^{\prime}_{A}$, Trent publishes the information of the decoy particles including their positions and correct states. Then, Alice measures all the decoy particles in $G^{\prime}_{A}$ and checks whether the measurement results are the same as those published by Trent. Once the error rate is above the established standards set by the system, the partners restart the protocol. Or Alice gets G_A from the sequence $G^{\prime}_{A}$ by deleting the decoy particles. G_A is kept by Alice as her private sequence.

1.2 Appendix A.2: Signing phase

Suppose that Alice will sign a classical message c = (0100101).

SS-1: Alice computes the message digest f(k||c) = m with her key k and the hash function f. Suppose $m=(1100)$. Then $m_{1}=m_{2}=1$ and $m_{3}=m_{4}=0$. After that, Alice prepares a particle sequence where the symbol “||” denotes the connection of the bit strings. After that, Alice prepares a particle sequence S = {s₁, s₂, s₃, s₄}, and the state of the i-th particle s_i of the sequence S is $\left| {s_{i} } \right\rangle = \left| {m_{i} } \right\rangle$. That is,

$$\left| {s_{1} } \right\rangle =\left| {s_{2} } \right\rangle= \left| {1} \right\rangle \, {\text{and}}\, \left| {s_{3} } \right\rangle =\left| {s_{4} } \right\rangle= \left| {0} \right\rangle.$$

SS-2: For the ith(i = 1, 2, 3, 4) operation, if k_i= 0, Alice executes the controlled NOT operator on a_i and s_i, where a_i is operated as the controlled particle, while s_i as the target particle.

For the ith(i = 1, 2, 3, 4) operation, if k_i= 1, Alice executes the operator H on a_i. Then, she performs the controlled NOT operation on a_i and s_i, where a_i is operated as the controlled particle, while s_i the target particle. Next, Alice performs the H operations on the particles a_i and s_i, respectively.

After that, the particles $t_{i}^{(T1)}$, $t_{i}^{(T2)}$, a_i and s_i are entangled together with the state as follows:

$$ \left\{ {\begin{array}{*{20}l} {\left| {\chi _{{t_{1}^{{(T1)}} ,t_{1}^{{(T2)}} ,a_{1} ,s_{1} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{1}^{{(T1)}} + _{1}^{{(T2)}} + _{1}^{A} - _{1}^{S} } \right\rangle + \left| { - _{1}^{{(T1)}} - _{1}^{{(T2)}} - _{1}^{A} {\text{ + }}_{1}^{S} } \right\rangle } \right)} \hfill \\ {\left| {\chi _{{t_{2}^{{(T1)}} ,t_{2}^{{(T2)}} ,a_{2} ,s_{2} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{2}^{{(T1)}} 0_{2}^{{(T2)}} 0_{2}^{A} 1_{2}^{S} } \right\rangle {\text{ }} + \left| {1_{2}^{{(T1)}} 1_{2}^{{(T2)}} 1_{2}^{A} 0_{2}^{S} } \right\rangle {\text{ }}} \right)} \hfill \\ {\left| {\chi _{{t_{3}^{{(T1)}} ,t_{3}^{{(T2)}} ,a_{3} ,s_{3} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{3}^{{(T1)}} 0_{3}^{{(T2)}} 0_{3}^{A} 0_{3}^{S} } \right\rangle {\text{ }} + \left| {1_{3}^{{(T1)}} 1_{3}^{{(T2)}} 1_{3}^{A} 1_{3}^{S} } \right\rangle {\text{ }}} \right)} \hfill \\ {\left| {\chi _{{t_{4}^{{(T1)}} ,t_{4}^{{(T2)}} ,a_{4} ,s_{4} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{4}^{{(T1)}} + _{4}^{{(T2)}} + _{4}^{A} + _{4}^{S} } \right\rangle + \left| { - _{4}^{{(T1)}} - _{4}^{{(T2)}} - _{4}^{A} - _{4}^{S} } \right\rangle } \right)} \hfill \\ \end{array} } \right., $$

(A2)

After that, Alice sends c and the particle sequence S to Bob. Bob keeps the particle sequence S as the quantum signature on c.

1.3 Appendix A.3: Verifying phase

VS-1: Bob publishes c = (0100101). Then, by the decoy particles and the methods in steps IS-3 and IS-4, Bob sends Trent the sequence S.

VS-2: According to the shared key k = (k₁, k₂, k₃, k₄) =  (1001), the particle sequences $G_{T1} = \{ t_{1}^{(T1)} , \, t_{2}^{(T1)} ,t_{3}^{(T1)} , \, t_{4}^{(T1)} \}$ and S = {s₁, s₂, s₃, s₄}, Trent performs four controlled unitary operations as follows.

For the ith(i = 1, 2, 3, 4) operation, if k_i = 0, Trent executes the controlled NOT operator on the controlled $t_{i}^{(T1)}$ and the target particle s_i.

For the ith (i = 1, 2, 3, 4) operation, if k_i = 1, Trent performs the H operations on the particles $t_{i}^{(T1)}$ and s_i, respectively. Then, he performs the controlled NOT operator on $t_{i}^{(T1)}$ and s_i so that $t_{i}^{(T1)}$ is operated as the controlled particle while s_i the target particle. At last, he applies operator H to $t_{i}^{(T1)}$.

After that, the entangled state of $t_{i}^{(T1)}$, $t_{i}^{(T2)}$, a_i and s_i (i = 1, 2, 3, 4) evolves into

$$ \left\{ \begin{gathered} \left| {\chi_{{t_{1}^{(T1)} ,t_{1}^{(T2)} ,a_{1} ,s_{1} }} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| { +_{1}^{(T1)} +_{1}^{(T2)} +_{1}^{A} } \right\rangle + \left| { -_{1}^{(T1)} -_{1}^{(T2)} -_{1}^{A} } \right\rangle } \right)\left| {1_{1}^{S} } \right\rangle \hfill \\ \left| {\chi_{{t_{2}^{(T1)} ,t_{2}^{(T2)} ,a_{2} ,s_{2} }} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {0_{2}^{(T1)} 0_{2}^{(T2)} 0_{2}^{A} } \right\rangle \, + \left| {1_{2}^{(T1)} 1_{2}^{(T2)} 1_{2}^{A} } \right\rangle \, } \right)\left| {1_{2}^{S} } \right\rangle \hfill \\ \left| {\chi_{{t_{3}^{(T1)} ,t_{3}^{(T2)} ,a_{3} ,s_{3} }} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {0_{3}^{(T1)} 0_{3}^{(T2)} 0_{3}^{A} } \right\rangle \, + \left| {1_{3}^{(T1)} 1_{3}^{(T2)} 1_{3}^{A} } \right\rangle \, } \right)\left| {0_{3}^{S} } \right\rangle \hfill \\ \left| {\chi_{{t_{4}^{(T1)} ,t_{4}^{(T2)} ,a_{4} ,s_{4} }} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| { +_{4}^{(T1)} +_{4}^{(T2)} +_{4}^{A} } \right\rangle + \left| { -_{4}^{(T1)} -_{4}^{(T2)} -_{4}^{A} } \right\rangle } \right)\left| {0_{4}^{S} } \right\rangle \hfill \\ \end{gathered} \right.. $$

(A3)

VS-3: Trent measures each particle s_i (i = 1, 2, 3, 4) with z-basis $\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\}$. By the measurement result of s_i, Trent sets $m^{\prime} = \left( {m^{\prime}_{1} ,m^{\prime}_{2} ,m^{\prime}_{3} ,m^{\prime}_{4} } \right)$, where.

$$ m_{i}^{\prime } = \left\{ \begin{gathered} 0,\quad {\text{if}}\,\,\left| {s_{i} } \right\rangle = \left| 0 \right\rangle \hfill \\ 1,\quad {\text{if}}\,\,\left| {s_{i} } \right\rangle = \left| 1 \right\rangle \hfill \\ \end{gathered} \right.. $$

(A4)

According to Eq. (A3), it is clear that $\left| {s_{1} } \right\rangle = \left| {s_{2} } \right\rangle = \left| 1 \right\rangle$ and $\left| {s_{3} } \right\rangle = \left| {s_{4} } \right\rangle = \left| 0 \right\rangle$. Therefore, Trent gets $m^{\prime } = \left( {1,1,0,0} \right)$. Then, by the shared k and the message c published by Bob, Trent can compute the message digest f(k||c) = m = (1100). Next, he checks whether $m = m^{\prime }$. If $m = m^{\prime }$ ($m \ne m^{\prime }$) Trent publishes “Yes”(“No”), and Bob accepts (denies) the validity of the quantum signature. If the signature is valid, Trent also keeps (c, m, Bob) as the “proof” of the quantum signature so as to solve the disputation that may occur between Alice and Bob in the future.

For this example, it is obvious that $m = m^{\prime }$. Then, the signature is valid. Thus, Trent keeps (c, m, Bob) as the “proof” of the quantum signature so as to solve the disputation that may occur between Alice and Bob in the future.

Appendix B: Analysis of the security

In this section, the example in Appendix A is used.

2.1 Appendix B.1: Information-theoretical security

Theorem 1.

The quantum signatures on all the messages have the same density operator.

According to the proposed scheme in Appendix A, we know that the quantum signature S on message c satisfies Eq. (A2). By Eq. (A2), we can get

$$ \left\{ \begin{gathered} \rho_{{s_{1} }} = \frac{1}{2}\left( {\left| { -_{1}^{S} } \right\rangle \left\langle { -_{1}^{S} } \right| + \left| { +_{1}^{S} } \right\rangle \left\langle { +_{1}^{S} } \right|} \right) = \frac{I}{2} \hfill \\ \rho_{{s_{2} }} = \frac{1}{2}\left( {\left| {1_{2}^{S} } \right\rangle \left\langle {1_{2}^{S} } \right| + \left| {0_{2}^{S} } \right\rangle \left\langle {0_{2}^{S} } \right|} \right) = \frac{I}{2} \hfill \\ \rho_{{s_{2} }} = \frac{1}{2}\left( {\left| {0_{3}^{S} } \right\rangle \left\langle {0_{3}^{S} } \right| + \left| {1_{3}^{S} } \right\rangle \left\langle {1_{3}^{S} } \right|} \right) = \frac{I}{2} \hfill \\ \rho_{{s_{4} }} = \frac{1}{2}\left( {\left| { +_{4}^{S} } \right\rangle \left\langle { +_{4}^{S} } \right| + \left| { -_{4}^{S} } \right\rangle \left\langle { -_{4}^{S} } \right|} \right) = \frac{I}{2} \hfill \\ \end{gathered} \right., $$

(A5)

Therefore, for the message c, the corresponding density operator of the signature S is $\rho_{s} = \frac{{ \otimes_{i = 1}^{4} I}}{{2^{4} }}$. Similarly, for any signature S on the message c, we can compute the same density operator $\rho_{s} = \frac{{ \otimes_{i = 1}^{4} I}}{{2^{4} }}$. Then, the correctness of Theorem 1 can be verified.

Theorem 2.

If an adversary Eve performs some unitary operator $U = \otimes_{i = 1}^{n} U_{i}$ on the signature S, the density operator of the signature will have not any change. That is, for each message–signature pair (c, S), after the unitary operator attack $U = \otimes_{i = 1}^{n} U_{i}$ on S, the density operator of the state of the disturbed quantum signature S is always $\rho_{s} = \frac{{ \otimes_{i = 1}^{n} I}}{{2^{n} }}$.

For the example, the signature S and the message c satisfy Eq. (A2). If an adversary Eve applies some unitary operator $U = \otimes_{i = 1}^{4} U_{i}$ to S, the density operator of s_i can be computed as follow.

$$ \left\{ \begin{gathered} \rho_{{s_{1} }} = \frac{1}{2}U_{1} \left( {\left| { -_{1}^{S} } \right\rangle \left\langle { -_{1}^{S} } \right| + \left| { +_{1}^{S} } \right\rangle \left\langle { +_{1}^{S} } \right|} \right)U_{1}^{ + } = \frac{I}{2} \hfill \\ \rho_{{s_{2} }} = \frac{1}{2}U_{2} \left( {\left| {1_{2}^{S} } \right\rangle \left\langle {1_{2}^{S} } \right| + \left| {0_{2}^{S} } \right\rangle \left\langle {0_{2}^{S} } \right|} \right)U_{2}^{ + } = \frac{I}{2} \hfill \\ \rho_{{s_{2} }} = \frac{1}{2}U_{3} \left( {\left| {0_{3}^{S} } \right\rangle \left\langle {0_{3}^{S} } \right| + \left| {1_{3}^{S} } \right\rangle \left\langle {1_{3}^{S} } \right|} \right)U_{3}^{ + } = \frac{I}{2} \hfill \\ \rho_{{s_{4} }} = \frac{1}{2}U_{4} \left( {\left| { +_{4}^{S} } \right\rangle \left\langle { +_{4}^{S} } \right| + \left| { -_{4}^{S} } \right\rangle \left\langle { -_{4}^{S} } \right|} \right)U_{4}^{ + } = \frac{I}{2} \hfill \\ \end{gathered} \right.. $$

Therefore, if an adversary Eve applies some unitary operator $U = \otimes_{i = 1}^{4} U_{i}$ to S, the density operator of the state of the disturbed quantum signatures S keeps as $\rho_{s} = \frac{{ \otimes_{i = 1}^{4} I}}{{2^{4} }}$. Therefore, for any unitary operator attack, the signature density operator will not have any change. Then, the correctness of Theorem 2 can be verified.

Theorem 3.

For any message c and unitary operator attack $U = \otimes_{i = 1}^{n} U_{i}$ on the signature S, the mutual information between private key space K and the probabilistic polynomial-time quantum adversary Eve is zero. That is,

$$ I\left( {K;{\text{Eve}}\left| {c, \, S, \, U} \right.} \right) = 0. $$

(A6)

Theorem 3 depends on the result of Theorem 2, Eq. (8) and the distribution of the key space for the key generated by the unconditional secure BB84 protocol. For the proof of Theorem 3, please refer to Sect. 3.1

Theorem 4

[55]. A quantum signature has information-theoretical security only if, for each polynomial p and different messages c and c^*, the trace distance.

$$ D(\rho_{c} ,\rho_{c*} ) < 1/p(n), $$

(A7)

where $\rho_{c}$($\rho_{{c^{*} }}$) denotes the density operator of the signature S (S^*) on c(c^*).

Theorem 5.

Our new AQS has the information-theoretical security.

Let c and c^* be any two different messages. Let S and S^* be the quantum signatures on the messages c and c^*, respectively. We use $\rho_{c}$ and $\rho_{{c^{*} }}$ denote the density operators of the states of the quantum signatures S and S^*, respectively. According to Theorem 1, it follows that $\rho_{c} = \rho_{{c^{*} }} = \frac{{ \otimes_{i = 1}^{4} I}}{{2^{4} }}$. Therefore,

$$ D(\rho_{c} ,\rho_{c*} ) = 0. $$

(A8)

It is clear that Eq. (A8) satisfies the result of Theorem 4. Therefore, our scheme can be of information-theoretical security.

2.2 Appendix B.2: Unforgeability

Theorem 6.

Given an entangled-triple sequence $\Pi = \left\{ {\pi_{1} ,\pi_{2} , \ldots ,\pi_{k} } \right\}$, in which each entangled $\pi_{i}$ (1 ≤ i ≤ k) is randomly selected in the set $\left\{ {\frac{1}{\sqrt 2 }\left( {\left| {000} \right\rangle + \left| {111} \right\rangle } \right),\frac{1}{\sqrt 2 }\left( {\left| { + + + } \right\rangle + \left| { - - - } \right\rangle } \right)} \right\}$, there is not any unitary operator W so that the sub-system of each $\pi_{i}$ can be cloned. That is, there is not any unitary operator W so that.

$$ W\left( {\frac{1}{\sqrt 2 }\left( {\left| {000} \right\rangle + \left| {111} \right\rangle } \right)\left| \varepsilon \right\rangle } \right) = \frac{1}{\sqrt 2 }\left( {\left| {0000} \right\rangle + \left| {1111} \right\rangle } \right) $$

and

$$ W\left( {\frac{1}{\sqrt 2 }\left( {\left| { + + + } \right\rangle + \left| { - - - } \right\rangle } \right)\left| \varepsilon \right\rangle } \right) = \frac{1}{\sqrt 2 }\left( {\left| { + + + + } \right\rangle + \left| { - - - - } \right\rangle } \right), $$

where $\varepsilon$ is an auxiliary particle.

The proof the Theorem 3 depends on the non-orthogonality of the states $\frac{1}{\sqrt 2 }\left( {\left| {000} \right\rangle + \left| {111} \right\rangle } \right)$ and $\frac{1}{\sqrt 2 }\left( {\left| { + + + } \right\rangle + \left| { - - - } \right\rangle } \right)$. For more detail proof of Theorem 3, please refer to Sect. 3.2.

Theorem 7.

Without the knowledge of the signer’s private key, it is not feasible for adversary Eve to produce a forged quantum signature.

For this example, the parameter n = 4 and the signer’s private key k = (k₁, k₂, k₃ k₄) = (1001). Thus, k₁ = k₄ = 1, k₂ = k₃ = 0. Suppose Eve is a quantum adversary, who plays the role of the forger. Note that Sect. 3.1has proved the information-theoretical security for the proposed AQS, which can ensure the secrecy of signatory’s key. For our scheme, to forge the quantum signature, Eve has to query the oracle f for its output. Suppose that Eve can successfully forge a signature S on some message c = (0101100) without knowing the signatory’s key k. And the answer for the output of the query on the oracle f about the message c is m = (0101). Note that if S is a valid forgery. Then, the forgery S must satisfy Eq. (A9) as follows:

$$ \left\{ {\begin{array}{*{20}l} {\left| {\chi _{{t_{1}^{{(T1)}} ,t_{1}^{{(T2)}} ,a_{1} ,s_{1} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{1}^{{(T1)}} + _{1}^{{(T2)}} + _{1}^{A} {\text{ + }}_{1}^{S} } \right\rangle + \left| { - _{1}^{{(T1)}} - _{1}^{{(T2)}} - _{1}^{A} - _{1}^{S} } \right\rangle } \right)} \hfill \\ {\left| {\chi _{{t_{2}^{{(T1)}} ,t_{2}^{{(T2)}} ,a_{2} ,s_{2} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{2}^{{(T1)}} 0_{2}^{{(T2)}} 0_{2}^{A} 1_{2}^{S} } \right\rangle {\text{ }} + \left| {1_{2}^{{(T1)}} 1_{2}^{{(T2)}} 1_{2}^{A} 0_{2}^{S} } \right\rangle {\text{ }}} \right)} \hfill \\ {\left| {\chi _{{t_{3}^{{(T1)}} ,t_{3}^{{(T2)}} ,a_{3} ,s_{3} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{3}^{{(T1)}} 0_{3}^{{(T2)}} 0_{3}^{A} 0_{3}^{S} } \right\rangle {\text{ }} + \left| {1_{3}^{{(T1)}} 1_{3}^{{(T2)}} 1_{3}^{A} 1_{3}^{S} } \right\rangle {\text{ }}} \right)} \hfill \\ {\left| {\chi _{{t_{4}^{{(T1)}} ,t_{4}^{{(T2)}} ,a_{4} ,s_{4} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{4}^{{(T1)}} + _{4}^{{(T2)}} + _{4}^{A} - _{4}^{S} } \right\rangle + \left| { - _{4}^{{(T1)}} - _{4}^{{(T2)}} - _{4}^{A} + _{4}^{S} } \right\rangle } \right)} \hfill \\ \end{array} } \right.. $$

(A9)

According to m = (0, 1, 0, 1) and the forged quantum signature S, Eve composes a new particle sequence $S|_{{m_{{i_{j} }} = 0}}$. That is, for each particle s_i (1 ≤ i ≤ 4) of the particle sequence S, if m_i = 0, Eve puts the particle s_i into the set $S|_{{m_{{i_{j} }} = 0}}$. Then,

$$S|_{{m_{{i_{j} }} = 0}} = \left\{ {s_{1} ,s_{3} } \right\}$$

(A10)

According to Eq. (A1), it follows that

$$ \Phi {\text{|}}_{{m_{{i_{j} }} = 0}} = \left\{ {\begin{array}{*{20}l} {\left| {\phi _{1} } \right\rangle {\text{ = }}\frac{1}{{\sqrt 2 }}\left( {\left| { + _{1}^{{(T1)}} + _{1}^{{(T2)}} + _{1}^{A} } \right\rangle + \left| { - _{1}^{{(T1)}} - _{1}^{{(T2)}} - _{1}^{A} } \right\rangle } \right)} \hfill \\ {\left| {\phi _{3} } \right\rangle {\text{ = }}\frac{1}{{\sqrt 2 }}\left( {\left| {0_{3}^{{(T1)}} 0_{3}^{{(T2)}} 0_{3}^{A} } \right\rangle {\text{ }} + \left| {1_{3}^{{(T1)}} 1_{3}^{{(T2)}} 1_{3}^{A} } \right\rangle {\text{ }}} \right)} \hfill \\ \end{array} } \right\}. $$

(A11)

After the successful forgery, Eve queries about the private particles indexed by 1 and 3, the signing system outputs the particle sequence $\Phi {|}_{{m_{{i_{j} }} = 0}}$ for Eve.

On the other hand, according to Eq. (A10) and the indexes 1 and 3, the signing system outputs a sequence

$$ \chi_{T1,T2,A,S} |_{{m_{{i_{j} }} = 0}} = \left\{ {\left| {\chi_{{t_{1}^{(T1)} ,t_{1}^{(T2)} ,a_{1} ,s_{1} }} } \right\rangle ,\left| {\chi_{{t_{3}^{(T1)} ,t_{3}^{(T2)} ,a_{3} ,s_{3} }} } \right\rangle } \right\}. $$

(A12)

Now, we compare the form of each particle of the particle sequence $\Phi {|}_{{m_{{i_{j} }} = 0}}$ with that of the particle sequence $\chi_{T1,T2,A,S} |_{{m_{{i_{j} }} = 0}}$. According to Eqs. (A9–A12), it follows that

$$ \left\{ {\begin{array}{*{20}l} {\left| {\phi _{1} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{1}^{{(T1)}} + _{1}^{{(T2)}} + _{1}^{A} } \right\rangle + \left| { - _{1}^{{(T1)}} - _{1}^{{(T2)}} - _{1}^{A} } \right\rangle } \right)} \hfill \\ {\left| {\chi _{{t_{1}^{{(T1)}} ,t_{1}^{{(T2)}} ,a_{1} ,s_{1} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| { + _{1}^{{(T1)}} + _{1}^{{(T2)}} + _{1}^{A} + _{1}^{S} } \right\rangle + \left| { - _{1}^{{(T1)}} - _{1}^{{(T2)}} - _{1}^{A} - _{1}^{S} } \right\rangle } \right)} \hfill \\ \end{array} } \right.. $$

(A13)

$$ \left\{ {\begin{array}{*{20}l} {\left| {\phi _{3} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{3}^{{(T1)}} 0_{3}^{{(T2)}} 0_{3}^{A} } \right\rangle {\text{ }} + \left| {1_{3}^{{(T1)}} 1_{3}^{{(T2)}} 1_{3}^{A} } \right\rangle {\text{ }}} \right)} \hfill \\ {\left| {\chi _{{t_{3}^{{(T1)}} ,t_{3}^{{(T2)}} ,a_{3} ,s_{3} }} } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {0_{3}^{{(T1)}} 0_{3}^{{(T2)}} 0_{3}^{A} 0_{3}^{S} } \right\rangle + \left| {1_{3}^{{(T1)}} 1_{3}^{{(T2)}} 1_{3}^{A} 1_{3}^{S} } \right\rangle } \right)} \hfill \\ \end{array} } \right.. $$

(A14)

According to Eqs. (A10, A11, A13, A14), we can get that if Eve can produce a valid forged signature S, he can clone a particle sequence $S|_{{m_{{i_{j} }} = 0}} = \left\{ {s_{1} ,s_{3} } \right\}$ from the entangled-triple sequence $\left\{ {\phi_{1} ,\phi_{3} } \right\}$, which is conflict to the non-cloning theorem (proved in Theorem 6) for the sub-system of each entangled $\phi_{{i_{j} }}$ of $\left\{ {\phi_{1} ,\phi_{3} } \right\}$. Therefore, it will be not feasible for Eve to forge the quantum signature of the signer.