Concurrence of two identical atoms in a rectangular waveguide: linear approximation with single excitation

Abstract

Waveguide electrodynamics has been attracted much attention; however, a waveguide with a cross section has seldom considered. We study two two-level systems (TLSs) interacting with a reservoir of guided modes confined in a rectangular waveguide of a cross section. For the energy separation of the identical TLSs far away from the cutoff frequencies of transverse modes, the delay differential equations are obtained with single-excitation initial in the TLSs. We accurately solved the delay differential equations for the TLSs interacting with either single transverse mode or double transverse modes of the waveguide. The retarded character of multiple reemissions and reabsorptions of photons between the TLSs is revealed, and the effects of the inter-TLS distance on the time evolution of the concurrence of the TLSs is examined.

Appendix

The detailed derivation of Eqs. (8) and (12).

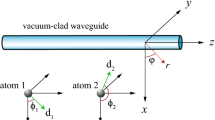
We consider a system of two two-level atoms weakly coupled to a rectangular hollow metallic waveguide made of perfect conductors. Under the dipolar and rotating wave approximation, the total Hamiltonian in the Schrö dinger picture is

$$\begin{aligned} H&=\sum _{l=1}^{2}\hbar \omega _{A}\sigma _{l}^{+}\sigma _{l}^{-}+\sum _{j}\int \mathrm{d}k\hbar \omega _{jk}{\hat{a}}_{jk}^{\dagger }{\hat{a}}_{jk}\nonumber \\&\quad +i\sum _{l=1}^{2}\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}}{\sqrt{\omega _{jk}}}\left( S_{l}^{-}{\hat{a}}_{jk}^{\dagger }e^{ikz_{l}}- S_{l}^{+}{\hat{a}}_{jk}e^{-ikz_{l}}\right) \end{aligned}$$

(24)

Any state of the two TLSs is linear superposition of the basis of the separable product states $\left| 1\right\rangle =\left| g_{1}g_{2}\right\rangle , \left| 2\right\rangle =\left| e_{1}g_{2}\right\rangle , \left| 3\right\rangle =\left| g_{1}e_{2}\right\rangle$ and $\left| 4\right\rangle =\left| e_{1}e_{2}\right\rangle .$ While in a single-excitation subspace, the basis $\left\{ \left| 20\right\rangle , \left| 30\right\rangle , {\hat{a}} _{jk}^{\dagger }\left| 10\right\rangle \right\}$ is complete to describe the system because the number of quanta is conserved. Here, $\left| 0\right\rangle$ is the vacuum state of the quantum field. So the wave function of the total system can be written as

$$\begin{aligned} \left| \psi (t)\right\rangle =b_{1}\left| 20\right\rangle +b_{2}\left| 30\right\rangle +\sum _{j}\int \mathrm{d}kb_{jk}{\hat{a}}_{jk}^{\dagger }\left| 10\right\rangle \end{aligned}$$

(25)

$b_{1}(t), b_{2}(t)$ and $b_{jk}(t)$ are corresponding amplitude. The wave function of the total system obeys the Schrödinger equation

$$\begin{aligned} i\hbar \frac{\partial \left| \psi (t)\right\rangle }{\partial t} =H\left| \psi (t)\right\rangle \end{aligned}$$

(26)

substituting Eqs. (24) and (25) into Eq. (26), we obtain

$$\begin{aligned}&{\dot{b}}_{1}\left| 20\right\rangle +{\dot{b}}_{2}\left| 30\right\rangle +\sum _{j}\int \mathrm{d}k{\dot{b}}_{jk}{\hat{a}}_{jk}^{\dagger }\left| 10\right\rangle \nonumber \\&\quad =-\frac{i}{\hbar }\left[ \sum _{l=1}^{2}\hbar \omega _{A}\sigma _{l}^{+} \sigma _{l}^{-}+\sum _{j}\int \mathrm{d}k\hbar \omega _{jk}{\hat{a}}_{jk}^{\dagger }{\hat{a}} _{jk}\right. \nonumber \\&\qquad +i\sum _{l=1}^{2}\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}}{\sqrt{\omega _{jk}}}( S_{l}^{-}{\hat{a}}_{jk}^{\dagger }e^{ikz_{l}} \nonumber \\&\qquad \left. -S_{l}^{+}{\hat{a}} _{jk}e^{-ikz_{l}})\right] \left( b_{1}\left| 20\right\rangle +b_{2}\left| 30\right\rangle +\sum _{j}\int \mathrm{d}kb_{jk}{\hat{a}}_{jk}^{\dagger }\left| 10\right\rangle \right) \nonumber \\&\quad =-i\omega _{A}b_{1}\left| 20\right\rangle -i\omega _{A}b_{2}\left| 30\right\rangle -i\sum _{j}\int \mathrm{d}k\omega _{jk}b_{jk}{\hat{a}} _{jk}^{\dagger }\left| 10\right\rangle \nonumber \\&\qquad +\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}b_{1}}{\sqrt{\omega _{jk}} }e^{ikz_{1}}{\hat{a}} _{jk}^{\dagger }\left| 10\right\rangle \nonumber \\&\qquad +\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}b_{2}}{\sqrt{\omega _{jk}}} e^{ikz_{2}}{\hat{a}} _{jk}^{\dagger }\left| 10\right\rangle \nonumber \\&\qquad -\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}b_{jk}}{ \sqrt{\omega _{jk}}}e^{-ikz_{1}}\left| 20\right\rangle -\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}b_{jk}}{\sqrt{\omega _{jk}}}e^{-ikz_{2}}\left| 30\right\rangle \nonumber \\&\quad =\left( -i\omega _{A}b_{1}-\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}b_{jk}}{\sqrt{\omega _{jk} }}e^{-ikz_{1}}\right) \left| 20\right\rangle \nonumber \\&\qquad +\left( -i\omega _{A}b_{2}-\sum _{j}\int \mathrm{d}k\hbar \frac{g_{j}b_{jk}}{\sqrt{\omega _{jk}}} e^{-ikz_{2}}\right) \left| 30\right\rangle \nonumber \\&\qquad +\sum _{j}\int \mathrm{d}k\left( -i\omega _{jk}b_{jk}+\frac{g_{j}b_{1}}{\sqrt{ \omega _{jk}}}e^{ikz_{1}}+\frac{g_{j}b_{2}}{\sqrt{\omega _{jk}}} e^{ikz_{2}}\right) {\hat{a}} _{jk}^{\dagger }\left| 10\right\rangle \end{aligned}$$

(27)

taking the overlap of the both sides of Eq. (27) with $\left\langle 20\right| , \left\langle 30\right|$ and $\left\langle 10\right| {\hat{a}} _{jk}$, respectively, gives

$$\begin{aligned} {\dot{b}}_{1}(t)&=-i\omega _{A}b_{1}(t)-\sum _{j}\int \mathrm{d}k\frac{g_{j}b_{jk}(t)}{\sqrt{ \omega _{jk}}}e^{-ikz_{1}} \end{aligned}$$

(28a)

$$\begin{aligned} {\dot{b}}_{2}(t)&=-i\omega _{A}b_{2}(t)-\sum _{j}\int \mathrm{d}k\frac{g_{j}b_{jk}(t)}{\sqrt{ \omega _{jk}}}e^{-ikz_{2}} \end{aligned}$$

(28b)

$$\begin{aligned} {\dot{b}}_{jk}(t)&=-i\omega _{jk}b_{jk}(t)+\frac{g_{j}}{\sqrt{\omega _{jk}}}[ b_{1}(t)e^{ikz_{1}}+b_{2}(t)e^{ikz_{2}}] \end{aligned}$$

(28c)

As the coupling strength is quite weak compared to the atomic frequency $\omega _{A}$ and field frequencies $\omega _{jk}$, we introduce three new variables to remove the high-frequency effect,

$$\begin{aligned} b_{1}(t)&=B_{1}(t)e^{-i\omega _{A}t}, \end{aligned}$$

(29a)

$$\begin{aligned} b_{2}(t)&=B_{2}(t)e^{-i\omega _{A}t}, \end{aligned}$$

(29b)

$$\begin{aligned} b_{jk}(t)&=B_{jk}\left( t\right) e^{-i\omega _{jk}t}, \end{aligned}$$

(29c)

using Eqs. (29), (28) become

$$\begin{aligned} {\dot{B}}_{1}(t)&=-\int \mathrm{d}k\frac{g_{j}B_{jk}(t)e^{-i\left( \omega _{jk}-\omega _{A}\right) t}}{\sqrt{\omega _{jk}}}e^{-ikz_{1}} \end{aligned}$$

(30a)

$$\begin{aligned} {\dot{B}}_{2}(t)&=-\int \mathrm{d}k\frac{g_{j}B_{jk}(t)e^{-i\left( \omega _{jk}-\omega _{A}\right) t}}{\sqrt{\omega _{jk}}}e^{-ikz_{2}} \end{aligned}$$

(30b)

$$\begin{aligned} {\dot{B}}_{jk}(t)&=\frac{g_{j}e^{ikz_{1}}}{\sqrt{\omega _{jk}}}[ B_{1}(t)+B_{2}(t)e^{ikz_{0}}]e^{i\left( \omega _{jk}-\omega _{A}\right) t} \end{aligned}$$

(30c)

where $z_{0}=z_{2}-z_{1}$. Integrating equation of $B_{jk}(t)$ and inserting it into the equations for $B_{1}(t)$ and $B_{2}(t),$ we have

$$\begin{aligned} {\dot{B}}_{1}(t)&=-\sum _{j}\int _{0}^{t}\mathrm{d}\tau \int \mathrm{d}k\frac{ g_{j}^{2}}{\omega _{jk}}[ B_{1}(\tau )+B_{2}(\tau )e^{ikz_{0}}] e^{-i\left( \omega _{jk}-\omega _{A}\right) \left( t-\tau \right) } \end{aligned}$$

(31a)

$$\begin{aligned} {\dot{B}}_{2}(t)&=-\sum _{j}\int _{0}^{t}\mathrm{d}\tau \int \mathrm{d}k\frac{ g_{j}^{2}}{\omega _{jk}}[ B_{1}(\tau )e^{-ikz_{0}}+B_{2}(\tau )] e^{-i\left( \omega _{jk}-\omega _{A}\right) \left( t-\tau \right) } \end{aligned}$$

(31b)

Then, take the linear expansion of dispersion relationship

$$\begin{aligned} \omega _{jk}&=\omega _{A}+v_{j}(k-k_{j0}),k>0 \end{aligned}$$

(32a)

$$\begin{aligned} \omega _{jk}&=\omega _{A}-v_{j}(k+k_{j0}),k<0 \end{aligned}$$

(32b)

into Eq. (31) and we assume the coefficient $\frac{ g_{j}^{2}}{\omega _{jk}}$ is independent with frequencies, $\frac{ g_{j}^{2}}{\omega _{jk}}\rightarrow \frac{ g_{j}^{2}}{\omega _{A}}$, which is a variant of Weisskopf–Wigner theory [54], Eq. (31) can be expressed as

$$\begin{aligned} {\dot{B}}_{\mu }(t)&=-\sum _{j}\frac{g_{j}^{2}}{\omega _{A}} \int _{0}^{t}\mathrm{d}\tau \int _{0}^{\infty }\mathrm{d}k[ B_{\mu }(\tau )+B_{\nu }(\tau )e^{i\times \left( -1\right) ^{\nu }kz_{0}}] e^{-iv_{j}(k-k_{j0})\left( t-\tau \right) }\nonumber \\&\quad -\sum _{j}\frac{g_{j}^{2}}{\omega _{A}} \int _{0}^{t}\mathrm{d}\tau \int _{-\infty }^{0}\mathrm{d}k[ B_{\mu }(\tau )+B_{\nu }(\tau )e^{i\times ( -1) ^{\nu }kz_{0}}] e^{iv_{j}(k+k_{j0})( t-\tau ) }\nonumber \\&=-\sum _{j}\frac{g_{j}^{2}}{\omega _{A}} \int _{0}^{t}\mathrm{d}\tau \int _{0}^{\infty }\mathrm{d}k[ B_{\mu }(\tau )+B_{\nu }(\tau )e^{i\times \left( -1\right) ^{\nu }kz_{0}}] e^{-iv_{j}(k-k_{j0})\left( t-\tau \right) }\nonumber \\&\quad -\sum _{j}\frac{g_{j}^{2}}{\omega _{A}} \int _{0}^{t}\mathrm{d}\tau \int _{0 }^{\infty }\mathrm{d}k[ B_{\mu }(\tau )+B_{\nu }(\tau )e^{-i\times ( -1) ^{\nu }kz_{0}}] e^{-iv_{j}(k-k_{j0})( t-\tau ) } \nonumber \\&=-\sum _{j}\gamma _{j}\int _{0}^{t}\mathrm{d}\tau \left[ 2B_{\mu }(\tau )\delta ( t-\tau ) +B_{\nu }(\tau )\delta \left( t-\tau -\frac{\left( -1\right) ^{\nu }z_{0}}{v_{j}}\right) \right. \nonumber \\&\quad \left. +B_{\nu }(\tau )\delta \left( t-\tau +\frac{\left( -1\right) ^{\nu }z_{0}}{v_{j}} \right) \right] e^{iv_{j}k_{j0}( t-\tau ) } \end{aligned}$$

(33)

where $\mu ,\nu =1,2(\mu \ne \nu )$, $\gamma _{j}=\frac{\pi g_{j}^{2}}{v_{j}\omega _{A}}$. The integral bound are approximated as $\int _{ 0}^{+\infty }\mathrm{d}k\simeq \frac{1}{2}\int _{-\infty }^{+\infty }\mathrm{d}k$, since we are only interested in photons with a narrow bandwidth in the vicinity of $\omega _{A}$ [55]. Then, from Eq. (33) we know that for $\mu =1,\nu =2$

$$\begin{aligned} {\dot{B}}_{1}(t)&=-\sum _{j}\gamma _{j}\int _{0}^{t}\mathrm{d}\tau \left[ 2B_{1}(\tau )\delta ( t-\tau )+B_{2}(\tau )\delta \left( t-\tau -\frac{z_{0}}{v_{j}}\right) \right. \nonumber \\&\quad \left. +B_{2}(\tau )\delta \left( t-\tau +\frac{z_{0}}{v_{j}} \right) \right] e^{iv_{j}k_{j0}( t-\tau ) } \nonumber \\&=-\sum _{j}\gamma _{j}\left[ B_{1}( t) + e^{ik_{j0}d}B_{2}\left( t-\frac{d}{ v_{j}}\right) \varTheta \left( t-\frac{d}{v_{j}}\right) \right] \end{aligned}$$

(34)

and for $\mu =2,\nu =1$

$$\begin{aligned} {\dot{B}}_{2}(t)&=-\sum _{j}\gamma _{j}\int _{0}^{t}\mathrm{d}\tau \left[ 2B_{2}(\tau )\delta \left( t-\tau \right) +B_{1}(\tau )\delta \left( t-\tau +\frac{z_{0}}{v_{j}}\right) \right. \nonumber \\&\quad \left. +B_{1}(\tau )\delta \left( t-\tau -\frac{z_{0}}{v_{j}} \right) \right] e^{iv_{j}k_{j0}( t-\tau ) } \nonumber \\&=-\sum _{j}\gamma _{j}\left[ B_{2}( t) +e^{ik_{j0}d}B_{1}\left( t-\frac{d}{ v_{j}}\right) \varTheta \left( t-\frac{d}{v_{j}}\right) \right] \end{aligned}$$

(35)

where $d=|z_{0}|$, $\varTheta (x)$ is the Heaviside unit step function and the formula $\int _{0}^{t}f(\tau )\delta (t-\tau )\mathrm{d}\tau =\frac{1}{2}f(t)$ is applied.