Abstract
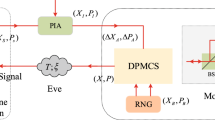
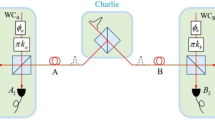
Continuous-variable quantum key distribution based on plug-and-play dual-phase-modulated coherent-states (DPMCS) protocol has been proved to be equivalent to the one-way Gaussian-modulated coherent-states protocol, but it is not just limited to this. This protocol can effectively against the LO-aimed attacks and maintain the system robust. However, the maximum transmission distance of the protocol is restricted due to its large excess noise. In this paper, we enhance the plug-and-play DPMCS protocol using quantum catalysis operation, which can be implemented by the existing technologies. To further highlight the advantage of the implementation of quantum catalysis operation, we make performance comparison not only between the proposed protocol and the original scheme but also the single-photon subtraction-based (SPS) plug-and-play DPMCS protocol. Security analysis shows that the proposed protocol can extend the maximum transmission distance up to hundreds of kilometers even under the effect of the imperfect source noise and show more excellent performance than the SPS-based plug-and-play DPMCS protocol. Furthermore, we also take the finite-size effect into consideration and thus achieve more practical results than those obtained in the asymptotic limit.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Lo, H.K., Curty, M., Tamaki, K.: Secure quantum key distribution. Nat. Photon. 8(8), 595 (2014)
Pirandola, S., Andersen, U. L., Banchi, L., Berta, M., Bunandar, D., Colbeck, R., Englund, D, Gehring, T., Lupo, C., Ottaviani, C., Pereira, J.: Advances in quantum cryptography. arXiv:1906.01645 (2019)
Scarani, V., Bechmann-Pasquinucci, H., Cerf, N.J., Dušek, M., Lütkenhaus, N., Peev, M.: The security of practical quantum key distribution. Rev. Mod. Phys. 81(3), 1301 (2009)
Weedbrook, C., Pirandola, S., García-Patrón, R., Cerf, N.J., Ralph, T.C., Shapiro, J.H., Lloyd, S.: Gaussian quantum information. Rev. Mod. Phys. 84, 621 (2012)
Grosshans, F., Grangier, P.: Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88(5), 057902 (2002)
Grosshans, F., Van Assche, G., Wenger, J., Brouri, R., Cerf, N.J., Grangier, P.: Quantum key distribution using Gaussian-modulated coherent states. Nature 421, 238 (2003)
Pirandola, S., Braunstein, S.L., Lloyd, S.: Characterization of collective Gaussian attacks and security of coherent-state quantum cryptography. Phys. Rev. Lett. 101(20), 200504 (2008)
Renner, R., Cirac, J.I.: de Finetti representation theorem for infinite-dimensional quantum systems and applications to quantum cryptography. Phys. Rev. Lett. 102(11), 110504 (2009)
Leverrier, A., Grosshans, F., Grangier, P.: Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 81(6), 062343 (2010)
Furrer, F., Franz, T., Berta, M., Leverrier, A., Scholz, V.B., Tomamichel, M., Werner, R.F.: Continuous variable quantum key distribution: finite-key analysis of composable security against coherent attacks. Phys. Rev. Lett. 109(10), 100502 (2012)
Leverrier, A.: Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 114(7), 070501 (2015)
Leverrier, A.: Security of continuous-variable quantum key distribution via a Gaussian de Finetti reduction. Phys. Rev. Lett. 118(20), 200501 (2017)
Huang, D., Huang, P., Lin, D., Zeng, G.: Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 6, 19201 (2016)
Jouguet, P., Kunz-Jacques, S., Leverrier, A., Grangier, P., Diamanti, E.: Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photon. 7(5), 378 (2013)
Zhang, Y., Li, Z., Chen, Z., Weedbrook, C., Zhao, Y., Wang, X., Huang, Y., Xu, C., Zhang, X., Wang, Z., Wang, G., Yu, S., Guo, H.: Continuous-variable QKD over 50 km commercial fiber. Quantum Sci. Technol. 4, 035006 (2019)
Huang, D., Huang, P., Li, H., Wang, T., Zhou, Y., Zeng, G.: Field demonstration of a continuous-variable quantum key distribution network. Opt. Lett. 41(15), 3511–3514 (2016)
Huang, J.Z., Weedbrook, C., Yin, Z.Q., Wang, S., Li, H.W., Chen, W., Guo, G.C., Han, Z.F.: Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 87(6), 062329 (2013)
Ma, X.C., Sun, S.H., Jiang, M.S., Liang, L.M.: Wavelength attack on practical continuous-variable quantum-key-distribution system with a heterodyne protocol. Phys. Rev. A 87(5), 052309 (2013)
Jouguet, P., Kunz-Jacques, S., Diamanti, E.: Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 87(6), 062313 (2013)
Qin, H., Kumar, R., Alléaume, R.: Saturation attack on continuous-variable quantum key distribution system. Proc. SPIE 8899, 88990N (2013)
Ma, X.C., Sun, S.H., Jiang, M.S., Liang, L.M.: Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 88(2), 022339 (2013)
Qi, B., Lougovski, P., Pooser, R., Grice, W., Bobrek, M.: Generating the local oscillator “locally” in continuous-variable quantum key distribution based on coherent detection. Phys. Rev. X 5(4), 041009 (2015)
Soh, D.B., Brif, C., Coles, P.J., Lütkenhaus, N., Camacho, R.M., Urayama, J., Sarovar, M.: Self-referenced continuous-variable quantum key distribution protocol. Phys. Rev. X 5(4), 041010 (2015)
Huang, D., Huang, P., Lin, D., Wang, C., Zeng, G.: High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 40(16), 3695–3698 (2015)
Huang, D., Huang, P., Wang, T., Li, H., Zhou, Y., Zeng, G.: Continuous-variable quantum key distribution based on a plug-and-play dual-phase-modulated coherent-states protocol. Phys. Rev. A 94(3), 032305 (2016)
Wu, X., Wang, Y., Liao, Q., Zhong, H., Guo, Y.: Simultaneous classical communication and quantum key distribution based on plug-and-play configuration with an optical amplifier. Entropy 21(4), 333 (2019)
Bartley, T.J., Crowley, P.J., Datta, A., Nunn, J., Zhang, L., Walmsley, I.: Strategies for enhancing quantum entanglement by local photon subtraction. Phys. Rev. A 87(2), 022313 (2013)
Wu, J., Liu, S., Hu, L., Huang, J., Duan, Z., Ji, Y.: Improving entanglement of even entangled coherent states by a coherent superposition of photon subtraction and addition. J. Opt. Soc. Am. B 32(11), 2299–2307 (2015)
Ourjoumtsev, A., Dantan, A., Tualle-Brouri, R., Grangier, P.: Increasing entanglement between Gaussian states by coherent photon subtraction. Phys. Rev. Lett. 98(3), 030502 (2007)
Huang, P., He, G., Fang, J., Zeng, G.: Performance improvement of continuous-variable quantum key distribution via photon subtraction. Phys. Rev. A 87(1), 012317 (2013)
Wu, X.D., Wang, Y.J., Zhong, H., Liao, Q., Guo, Y.: Plug-and-play dual-phase-modulated continuous-variable quantum key distribution with photon subtraction. Front. Phys. 14(4), 41501 (2019)
Peng, Q., Wu, X., Guo, Y.: Improving eight-state continuous variable quantum key distribution by applying photon subtraction. Appl. Sci. 9(7), 1333 (2019)
Li, Z., Zhang, Y., Wang, X., Xu, B., Peng, X., Guo, H.: Non-Gaussian postselection and virtual photon subtraction in continuous-variable quantum key distribution. Phys. Rev. A 93(1), 012310 (2016)
Liao, Q., Guo, Y., Huang, D., Huang, P., Zeng, G.H.: Long-distance continuous-variable quantum key distribution using non-Gaussian state-discrimination detection. New J. Phys. 20, 023015 (2018)
Ma, H.X., Huang, P., Bai, D.Y., Wang, S.Y., Bao, W.S., Zeng, G.: Continuous-variable measurement-device-independent quantum key distribution with photon subtraction. Phys. Rev. A 97(4), 042329 (2018)
Guo, Y., Liao, Q., Wang, Y.J., Huang, D., Huang, P., Zeng, G.H.: Performance improvement of continuous-variable quantum key distribution with an entangled source in the middle via photon subtraction. Phys. Rev. A 95, 032304 (2017)
Zhao, Y., Zhang, Y., Xu, B., Yu, S., Guo, H.: Continuous-variable measurement-device-independent quantum key distribution with virtual photon subtraction. Phys. Rev. A 97(4), 042328 (2018)
Lvovsky, A.I., Mlynek, J.: Quantum-optical catalysis: generating nonclassical states of light by means of linear optics. Phys. Rev. Lett. 88(25), 250401 (2002)
Guo, Y., Ye, W., Zhong, H., Liao, Q.: Continuous-variable quantum key distribution with non-Gaussian quantum catalysis. Phys. Rev. A 99(3), 032327 (2019)
Lee, S.Y., Ji, S.W., Kim, H.J., Nha, H.: Enhancing quantum entanglement for continuous variables by a coherent superposition of photon subtraction and addition. Phys. Rev. A 84(1), 012302 (2011)
Pirandola, S., Laurenza, R., Ottaviani, C., Banchi, L.: Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017)
Usenko, V.C., Filip, R.: Feasibility of continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 81, 022318 (2010)
Shen, Y., Peng, X., Yang, J., Guo, H.: Continuous-variable quantum key distribution with Gaussian source noise. Phys. Rev. A 83, 052304 (2011)
Wu, X., Wang, Y., Li, S., Zhang, W., Huang, D., Guo, Y.: Security analysis of passive measurement-device-independent continuous-variable quantum key distribution with almost no public communication. Quantum Inf. Process. 18(12), 372 (2019)
Derkach, I., Usenko, V.C., Filip, R.: Continuous-variable quantum key distribution with a leakage from state preparation. Phys. Rev. A 96, 062309 (2017)
Wu, X., Wang, Y., Huang, D.: Passive continuous-variable quantum secret sharing using a thermal source. Phys. Rev. A 101(2), 022301 (2020)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61801522) and National Nature Science Foundation of Hunan Province, China (Grant No. 2019JJ40352).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Calculation of asymptotic secret key rate
Now let us calculate the asymptotic secret key rate. Without loss of generality, we suppose Bob performs homodyne detection. Taking the reverse reconciliation into consideration, the asymptotic secret key rate is given by
where I(A : B) represents the Shannon mutual information between Alice and Bob, \(\chi (A:E)\) represents the Holevo bound between Alice and Eve, \(\beta \) stands for the reconciliation efficiency for reverse reconciliation, and \(P_{t}\) stands for the success probability of implementing SSQC operation.
After passing through the untrusted quantum channel and Alice’s detection, the covariance matrix of \(\rho _{\mathrm{FBA}_{2}}\) reads
The Shannon mutual information shared by Alice and Bob \(I_{AB}\) is given by
with \(V_{B}=(\vartheta +1)/2\), \(V_{A}=\lambda \), and
Since Eve can purify the system \(\mathrm{FBA}_{2}\) and Alice can employ her measurement to purify the system FBE, thus we have
where \(G(x)=(x+1)\log _{2}(x+1)-x\log _{2}x\), and the symplectic eigenvalues \(\nu _{1,2}\) is given by
with
The symplectic eigenvalue \(\nu _{3}\) is expressed as \(\nu _{3}=\sqrt{\vartheta ^{2}-\vartheta \kappa ^{2}/\lambda }\). According to above analysis, we can calculate the asymptotic secret key rate in Eq. (8).
Appendix B: Finite-size secret key rate
For the proposed protocol, the finite-size secret key rate is given by [9]
where \(\beta \) and I(A : B) are as the same as the aforementioned definitions. N stands for the total exchanged signals, and n stands for the number of signals which is taken advantage of for derivation of QKD. Note that the remained signals \(f=N-n\) are utilized to perform parameter estimation. \(\epsilon _{\mathrm{PE}}\) stands for the failure probability of parameter estimation and \(\chi _{\epsilon _{\mathrm{PE}}}(A:E)\) stands for the maximal value of the Holevo information in finite-size scenario. \(\varDelta (n)\) is related to the security of the privacy amplification, which is given by
where \(\bar{\epsilon }\) and \(\epsilon _{\mathrm{PB}}\) stand for, respectively, the smoothing parameter and the failure probability of privacy amplification, and the Hilbert space dim \(H_{A}=2\).
To determine \(\chi _{\epsilon _{\mathrm{PE}}}(A:E)\), we need to construct the covariance matrix \(\varXi _{\epsilon _{\mathrm{PE}}}\) in parameter estimation procedure. Therefore, f couples of correlated variables \((x_{i},y_{i})_{i=1...f}\) are sampled and a normal model is taken advantage of for these correlated variables to link Alice and Bob’s data, which is given by
where \(\tau =\sqrt{T}\) and z follows a centered normal distribution with variance \(\delta ^{2}=1+T\zeta \). Then, the covariance matrix \(\varXi _{\epsilon _{\mathrm{PE}}}\) is given by
where \(\tau _{\mathrm{min}}\) and \(\delta ^{2}_{\mathrm{max}}\) represent minimum of \(\tau \) and maximum of \(\delta ^{2}\), respectively. It is remarkable that the maximum-likelihood estimators \(\hat{\tau }\) and \(\hat{\delta }^{2}\), respectively, can be calculated by
Besides, the following distributions
mean that the estimators \(\hat{\tau }\) and \(\hat{\delta }^{2}\) are independent for each other. Since parameters \(\tau \) and \(\delta ^{2}\) shown in Eq. (20) are true values, we can calculate \(\tau _{\mathrm{min}}\) (the lower bound of \(\tau \)) and \(\delta ^{2}_{\mathrm{max}}\) (the upper bound of \(\delta ^{2}\)), which is expressed as
where \(z_{\epsilon _{\mathrm{PE}}/2}\) is such that \(1-erf(z_{\epsilon _{\mathrm{PE}}/2}/\sqrt{2})/2=\epsilon _{\mathrm{PE}}/2\), and \(erf(x)=\frac{2}{\sqrt{\pi }}\int ^{x}_{0}e^{-t^{2}}dt\) is error function. Theoretically, the expected values of \(\hat{\tau }\) and \(\hat{\delta }^{2}\) read
Consequently, \(\tau _{\mathrm{min}}\) and \(\delta ^{2}_{\mathrm{max}}\) can be given by
It is worth mentioning that we can take the optimal value of the error probabilities as [9]
After that, the finite-size secret key rate can be calculated through utilizing the derived bounds \(\tau _{\mathrm{min}}\) and \(\delta ^{2}_{\mathrm{max}}\).
Rights and permissions
About this article
Cite this article
Wu, X., Wang, Y., Zhong, H. et al. Performance improvement of plug-and-play dual-phase-modulated continuous-variable quantum key distribution with quantum catalysis. Quantum Inf Process 19, 234 (2020). https://doi.org/10.1007/s11128-020-02730-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-020-02730-5