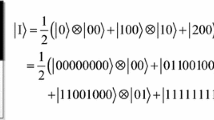Quantum realization of the nearest-neighbor interpolation method for FRQI and NEQR | Quantum Information Processing Skip to main content
Springer Nature Link
Log in

Quantum realization of the nearest-neighbor interpolation method for FRQI and NEQR

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

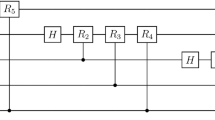
This paper is concerned with the feasibility of the classical nearest-neighbor interpolation based on flexible representation of quantum images (FRQI) and novel enhanced quantum representation (NEQR). Firstly, the feasibility of the classical image nearest-neighbor interpolation for quantum images of FRQI and NEQR is proven. Then, by defining the halving operation and by making use of quantum rotation gates, the concrete quantum circuit of the nearest-neighbor interpolation for FRQI is designed for the first time. Furthermore, quantum circuit of the nearest-neighbor interpolation for NEQR is given. The merit of the proposed NEQR circuit lies in their low complexity, which is achieved by utilizing the halving operation and the quantum oracle operator. Finally, in order to further improve the performance of the former circuits, new interpolation circuits for FRQI and NEQR are presented by using Control-NOT gates instead of a halving operation. Simulation results show the effectiveness of the proposed circuits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Benioff, P.: The computer as a physical system: a microscopic quantum mechanical Hamiltonian models of computers as represented by Turing machines. J. Stat. Phys. 22(5), 563–591 (1980)

    Article  MathSciNet  ADS  Google Scholar 

  2. Feynman, R.P.: Simulating physics with computers. Int. J. Theor. Phys. 21(6/7), 467–488 (1982)

    Article  MathSciNet  Google Scholar 

  3. Venegas-Andraca, S.E., Bose, S.: Storing, processing and retrieving an image using quantum mechanics. Proc. SPIE Conf. Quantum Inf. Comput. 5105, 137–147 (2003)

    ADS  Google Scholar 

  4. Venegas-Andraca, S.E., Ball, J.L.: Processing images in entangled quantum systems. Quantum Inf. Process. 9(1), 1–11 (2010)

    Article  MathSciNet  Google Scholar 

  5. Latorre, J.I.: Image compression and entanglement. arXiv:quant-ph/0510031 (2005)

  6. Le, P.Q., Dong, F., Hirota, K.: A flexible representation of quantum images for polynomial preparation, image compression and processing operations. Quantum Inf. Process. 10(1), 63–84 (2010)

    Article  MathSciNet  Google Scholar 

  7. Sun,B., Le, P.Q., Iliyasu, A.M., et al.: A multi-channel representation for images on quantum computers using the RGB \(\alpha \) color space. In: Proceedings of the IEEE 7th International Symposium on Intelligent Signal Processing, pp 1–6 (2011)

  8. Zhang, Y., Lu, K., Gao, Y.H., Xu, K.: A novel quantum representation for log-polar images. Quantum Inf. Process. 12(9), 3103–3126 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  9. Zhang, Y., Lu, K., Gao, Y.H., Wang, M.: NEQR: a novel enhanced quantum representation of digital images. Quantum Inf. Process. 12(8), 2833–2860 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  10. Iliyasu, A.M., Le, P.Q., Dong, F., et al.: Watermarking and authentication of quantum images based on restricted geometric transformation. Inf. Sci. 186(1), 126–149 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  11. Zhang, W.W., Gao, F., Liu, B., Jia, H.Y., Wen, Q., Chen, H.: A quantum watermark protocol. Int. J. Theor. Phys. 52(2), 504–513 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  12. Zhang, W.W., Gao, F., Liu, B., Wen, Q., Chen, H.: A watermark strategy for quantum images based on quantum Fourier transform. Quantum Inf. Process. 12(2), 793–803 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  13. Zhou, R.G., Wu, Q., Zhang, M.Q., et al.: Quantum image encryption and decryption algorithms based on quantum image geometric transformations. Int. J. Theor. Phys. 52(6), 1802–1817 (2013)

    Article  MathSciNet  Google Scholar 

  14. Yang, Y.G., Xia, J., Jia, X., et al.: Novel image encryption/decryption based on quantum Fourier transform and double phase encoding. Quantum Inf. Process. 12(11), 3477–3493 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  15. Yang, Y.G., Jia, X., Sun, S., et al.: Quantum cryptographic algorithm for color images using quantum Fourier transform and double random-phase encoding. Inf. Sci. 277, 445–457 (2014)

    Article  Google Scholar 

  16. Song, X.H., Wang, S., El-latif, A.A.A., Niu, X.M.: Quantum image encryption based on restricted geometric and color transformations. Quantum Inf. Process. 13(8), 1765–1787 (2014)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  17. Jiang, N., Wu, W.Y., Wang, L.: The quantum realization of Arnold and Fibonacci image scrambling. Quantum Inf. Process. 13(5), 1223–1236 (2014)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  18. Jiang, N., Wang, L.: Analysis and improvement of the quantum Arnold image scrambling. Quantum Inf. Process. 13(5), 1545–1551 (2014)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  19. Jiang, N., Wang, L., Wu, W.Y.: Quantum Hilbert image scrambling. Int. J. Theor. Phys. 53(7), 2463–2484 (2014)

    Article  MATH  Google Scholar 

  20. Le, P.Q., Iliyasu, A.M., Dong, F.Y., Hirota, K.: Fast geometric transformations on quantum images. Int J. Appl. Math. 40(3), 113–123 (2010)

    MATH  MathSciNet  Google Scholar 

  21. Nielson, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2010)

    Book  Google Scholar 

  22. Fijany, A., Williams, C.: Quantum wavelet transform: fast algorithm and complete circuits. arXiv:quant-ph/9809004 (1998)

  23. Klappenecker, A., Rötteler, M.: Discrete cosine transforms on quantum computers. In: IEEE8-EURASIP Symposium on Image and Signal Processing and Analysis (ISPA01), Pula, Croatia, pp. 464–468 (2001)

  24. Tseng, C.C., Hwang, T.M.: Quantum circuit design of \(8 \times 8\) discrete cosine transform using its fast computation flow graph. In: IEEE International Symposium on Circuits and Systems, 2005 (ISCAS 2005), pp. 828–831 (2005)

  25. Wang, J., Jiang, N., Wang, L.: Quantum image translation. Quantum Inf. Process. 14(5), 1589–1604 (2014)

    Article  ADS  Google Scholar 

  26. Jiang, N., Wang, L.: Quantum image scaling using nearest neighbor interpolation. Quantum Inf. Process. 14(5), 1559–1571 (2014)

    Article  ADS  Google Scholar 

  27. Zhang, Y., Lu, K., Xu, K., Gao, Y.H.: Local feature point extraction for quantum images. Quantum Inf. Process. 14(5), 1573–1588 (2014)

    Article  MathSciNet  ADS  Google Scholar 

  28. Barenco, A., Bennett, C.H., Cleve, R., DiVincenzp, D.P., Margolus, N., Shor, P., Sleator, T., Smolin, J.A., Weinfurther, H.: Elementary gates for quantum computation. Phys. Rev. A. 52(5), 3457 (1995)

    Article  ADS  Google Scholar 

Download references

Acknowledgments

This work is supported by the National Science Foundation of China (61301099, 60832010, 61501148 and 61361166006). We thank the previous researchers’ work about nearest-neighbor interpolation method for INEQR. Thanks are due to many anonymous reviewers for their assistance with the discussion about the improved circuits and the simulation results.

Author information

Authors and Affiliations

  1. Department of Computer Science and Technology, Harbin Institute of Technology, Harbin, China

    Jianzhi Sang, Shen Wang & Xiamu Niu

Authors
  1. Jianzhi Sang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiamu Niu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiamu Niu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sang, J., Wang, S. & Niu, X. Quantum realization of the nearest-neighbor interpolation method for FRQI and NEQR. Quantum Inf Process 15, 37–64 (2016). https://doi.org/10.1007/s11128-015-1135-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-015-1135-5

Keywords

Search

Navigation