Adiabatic quantum programming: minor embedding with hard faults | Quantum Information Processing
Skip to main content
Springer Nature Link
Log in

Adiabatic quantum programming: minor embedding with hard faults

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

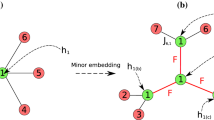
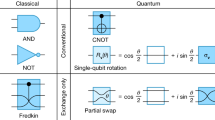
Abstract

Adiabatic quantum programming defines the time-dependent mapping of a quantum algorithm into an underlying hardware or logical fabric. An essential step is embedding problem-specific information into the quantum logical fabric. We present algorithms for embedding arbitrary instances of the adiabatic quantum optimization algorithm into a square lattice of specialized unit cells. These methods extend with fabric growth while scaling linearly in time and quadratically in footprint. We also provide methods for handling hard faults in the logical fabric without invoking approximations to the original problem and illustrate their versatility through numerical studies of embeddability versus fault rates in square lattices of complete bipartite unit cells. The studies show that these algorithms are more resilient to faulty fabrics than naive embedding approaches, a feature which should prove useful in benchmarking the adiabatic quantum optimization algorithm on existing faulty hardware.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Adler, I., et al.: Faster parameterized algorithms for minor containment. Theor. Comput. Sci. 412, 7018–7028 (2011)

    Article  MATH  Google Scholar 

  2. Altshuler, B., Karvi, H., Roland, J.: Anderson localization makes adiabatic quantum optimization fail. Proc. Natl. Acad. Sci. USA 108, E19–E20 (2011)

    Article  Google Scholar 

  3. Amir, E.: Approximation algorithms for treewidth. Algorithmica 56, 448–479 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bian, Z., Chudak, F., Macready, W.G., Clark, L., Gaitan, F.: Experimental determination of Ramsey numbers. Phys. Rev. Lett. 111, 130505 (2013)

    Google Scholar 

  5. Bodlaender, H.L.: A tourist guide through treewidth. Acta Cybern. 11, 1–23 (1993)

    MathSciNet  MATH  Google Scholar 

  6. Bodlaender, H.L.: A linear-time algorithm for finding tree decompositions of small treewidth. SIAM J. Comput. 25, 1035–1317 (1996)

    Article  MathSciNet  Google Scholar 

  7. Bodlaender, H.L., Koster, A.M.C.A.: Treewidth Computations II. Lower Bounds, Technical Report UU-CS-2010-022. Department of Information and Computing Sciences, Utrecht University (2010)

  8. Boros, E., Hammer, P.L.: Pseudo-boolean optimization. Discret. Appl. Math. 123, 155–225 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  9. Choi, V.: Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quantum Inf. Process. 7, 193–209 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  10. Choi, V.: Minor-embedding in adiabatic quantum computation: II. Minor-universal graph design. Quantum Inf. Process. 10, 343–353 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Dickson, N.G., Amin, M.H.S.: Does adiabatic quantum optimization fail for NP-complete problems? Phys. Rev. Lett. 106, 050502 (2011)

    Google Scholar 

  12. Dickson, N.G., Amin, M.H.S.: Algorithmic approach to adiabatic quantum optimization. Phys. Rev. A 85, 032303 (2012)

    Google Scholar 

  13. Diestel, R.: Graph Theory. Springer, Heidelberg (2005)

    MATH  Google Scholar 

  14. D-Wave Systems Inc., 100–4401 Still Creek Drive, Burnaby V5C 6G9, BC, Canada. http://www.dwavesys.com/

  15. Farhi, E., Goldstone, J., Gutmann, S., Sipser, M.: Quantum computation by adiabatic evolution, arxiv:quant-ph/0001106 (2000)

  16. Farhi, E., et al.: A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–476 (2001)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  17. Fomin, F.V., Thilikos, D.M.: Dominating sets and local treewidth. LNCS 2832, 221–229 (2003)

    MathSciNet  Google Scholar 

  18. Gaitan, F., Clark, L.: Ramsey numbers and adiabatic quantum computing. Phys. Rev. Lett. 108, 010501 (2012)

    Google Scholar 

  19. Harris, R., et al.: Experimental investigation of an eight qubit unit cell in a superconducting optimization processor. Phys. Rev. B 82, 024511–024526 (2010)

    Article  ADS  Google Scholar 

  20. Kleinberg, J., Rubinfeld, R.: Short paths in expander graphs. In: Proceedings of the 37th Annual Symposium on Foundations of Computer Science, pp. 86–95 (1996)

  21. Neven, H., Rose, G., Macready, W.G.: Image recognition with an adiabatic quantum computer I. Mapping to quadratic unconstrained binary optimization, arXiv:0804.4457v1 [quant-ph] (2008)

  22. Perdomo-Ortiz, A., Dickson, N., Drew-Brook, M., Rose, G., Aspuru-Guzik, A.: Finding low-energy conformations of lattice protein models by quantum annealing. Sci. Rep. 2, 571 (2012)

  23. Pudenz, K.L., Lidar, D.A.: Quantum adiabatic machine learning. Quantum Inf. Process. 12, 2027–2070 (2012)

  24. Robertson, N., Seymour, P.D.: Graph minors. XIII: the disjoint paths problem. J. Comb. Theory Ser. B 63, 65–110 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  25. Xiong, L., Dinneen, M.J.: The Feasibility and Use of a Minor Containment Algorithm, Computer Science Technical Reports 171, University of Auckland (2000)

Download references

Acknowledgments

This work was supported by the Lockheed Martin Corporation under Contract No. NFE-11-03394. The authors thank Greg Tallant (Lockheed) for technical interchange and Daniel Pack (ORNL) for help preparing Fig. 2. This manuscript has been authored by a contractor of the U.S. Government under Contract No. DE-AC05-00OR22725. Accordingly, the U.S. Government retains a non-exclusive, royalty-free license to publish or reproduce the published form of this contribution, or allow others to do so, for U.S. Government purposes.

Author information

Author notes

  1. Blair D. Sullivan

    Present address: Department of Computer Science, North Carolina State University, Raleigh, NC , 27695, USA

Authors and Affiliations

  1. Department of Mathematics and Computer Science, Emory University, 400 Dowman Drive, Atlanta, GA , 30322, USA

    Christine Klymko

  2. Oak Ridge National Laboratory, Quantum Computing Institute, 1 Bethel Valley Road, Oak Ridge, TN , 37831, USA

    Blair D. Sullivan & Travis S. Humble

Authors
  1. Christine Klymko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Blair D. Sullivan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Travis S. Humble
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Travis S. Humble.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Klymko, C., Sullivan, B.D. & Humble, T.S. Adiabatic quantum programming: minor embedding with hard faults. Quantum Inf Process 13, 709–729 (2014). https://doi.org/10.1007/s11128-013-0683-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-013-0683-9

Keywords

Search

Navigation