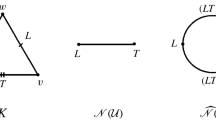Abstract
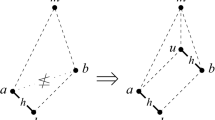
The classical way to study a finite poset (X, ≤ ) using topology is by means of the simplicial complex Δ X of its nonempty chains. There is also an alternative approach, regarding X as a finite topological space. In this article we introduce new constructions for studying X topologically: inspired by a classical paper of Dowker (Ann Math 56:84–95, 1952), we define the simplicial complexes K X and L X associated to the relation ≤. In many cases these polyhedra have the same homotopy type as the order complex Δ X . We give a complete characterization of the simplicial complexes that are the K or L-complexes of some finite poset and prove that K X and L X are topologically equivalent to the smaller complexes K′ X , L′ X induced by the relation <. More precisely, we prove that K X (resp. L X ) simplicially collapses to K′ X (resp. L′ X ). The paper concludes with a result that relates the K-complexes of two posets X, Y with closed relations R ⊂ X × Y.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alexandroff, P.S.: Diskrete Räume. MathematiceskiiSbornik (N.S.) 2, 501–518 (1937)
Bak, A., Brown, R., Minian, E.G., Porter, T.: Global actions, groupoid atlases and applications. J. Homotopy Relat. Struct. 1, 101–167 (2006)
Barmak, J.A., Minian, E.G.: 2-Dimension from the topological viewpoint. Order 24, 49–58 (2007)
Barmak, J.A., Minian, E.G.: Minimal finite models. J. Homotopy Relat. Struct. 2, 127–140 (2007)
Barmak, J.A., Minian, E.G.: Simple homotopy types and finite spaces. Adv. Math. 218, 87–104 (2008)
Björner, A.: Topological methods. In: Graham, R., Grötschel, M., Lovász, L. (eds.) Handbook of Combinatorics. Elsevier, New York (1995)
Cohen, M.M.: A Course in Simple Homotopy Theory. Springer-Verlag, New York (1970)
del Hoyo, M., Minian, E.G.: Classical invariants for global actions and groupoid atlases. Appl. Categ. Struct. 16(6), 689–721 (2008)
Dowker, C.H.: Homology groups of relations. Ann. Math. 56, 84–95 (1952)
Kozlov, D.: Combinatorial Algebraic Topology. Algorithms and Computation in Mathematics, vol. 21. Springer, Berlin (2008)
May, J.P.: Finite topological spaces. Notes for REU (2003). Available at http://www.math.uchicago.edu/may/MISCMaster.html
McCord, M.C.: Singular homology groups and homotopy groups of finite topological spaces. Duke Math. J. 33, 465–474(1966)
McCord, M.C.: Homotopy type comparison of a space with complexes associated with its open covers. Proc. Am. Math. Soc. 18(4), 705–708 (1967)
Milnor, J.: Whitehead Torsion. Bull. Amer. Math. Soc. 72, 358–426 (1966)
Quillen, D.: Higher algebraic K-theory I. Lect. Notes Math. 341, 85–147 (1973)
Quillen, D.: Homotopy properties of the poset of non-trivial p-subgroups of a group. Adv. Math. 28, 101–128 (1978)
Segal, G.: Classifying spaces and spectral sequences. Inst. Hautes Etudes Sci. Publ. Math. 34, 105–112 (1968)
Siebenmann, L.C.: Infinite simple homotopy types. Indag. Math. 32, 479–495 (1970)
Spanier, E.: Algebraic Topology. McGraw Hill, New York (1966)
Stanley, R.: Enumerative Combinatorics, vol. 1. Cambrdige Studies in Advanced Mathematics, 49. Cambridge University Press, Cambridge (1997)
Stong, R.E.: Finite topological spaces. Trans. Am. Math. Soc. 123, 325–340 (1966)
Whitehead, J.H.C.: Simplicial spaces, nuclei and m-groups. Proc. Lond. Math. Soc. 45, 243–327 (1939)
Whitehead, J.H.C.: On incidence matrices, nuclei and homotopy types. Ann. Math. 42, 1197–1239 (1941)
Whitehead, J.H.C.: Simple homotopy types. Am. J. Math. 72, 1–57 (1950)
Zeeman, E.C.: On the dunce hat. Topology 2, 341–358 (1964)
Author information
Authors and Affiliations
Corresponding author
Additional information
E.G. Minian’s research is partially supported by Conicet and by grant ANPCyT PICT 17-38280.
Rights and permissions
About this article
Cite this article
Minian, E.G. The Geometry of Relations. Order 27, 213–224 (2010). https://doi.org/10.1007/s11083-010-9146-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11083-010-9146-4