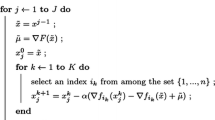Abstract
In this paper, we consider a regularized least squares problem subject to convex constraints. Our algorithm is based on the superiorization technique, equipped with a new step size rule which uses subgradient projections. The superiorization method is a two-step method where one step reduces the value of the penalty term and the other step reduces the residual of the underlying linear system (using an algorithmic operator T). For the new step size rule, we present a convergence analysis for the case when T belongs to a large subclass of strictly quasi-nonexpansive operators. To examine our algorithm numerically, we consider box constraints and use the total variation (TV) functional as a regularization term. The specific test cases are chosen from computed tomography using both noisy and noiseless data. We compare our algorithm with previously used parameters in superiorization. The T operator is based on sequential block iteration (for which our convergence analysis is valid), but we also use the conjugate gradient method (without theoretical support). Finally, we compare with the well-known “fast iterative shrinkage-thresholding algorithm” (FISTA). The numerical results demonstrate that our new step size rule improves previous step size rules for the superiorization methodology and is competitive with, and in several instances behaves better than, the other methods.








Similar content being viewed by others
References
Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38(3), 367–426 (1996)
Beck, A., Guttmann-Beck, N.: FOM–a MATLAB toolbox of first-order methods for solving convex optimization problems. Optim. Methods Softw 34(1), 172–193 (2019)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2(1), 183–202 (2009)
Björck, Å.: Numerical Methods for Least Squares Problems, vol. 51. SIAM, Philadelphia (1996)
Butnariu, D., Davidi, R., Herman, G.T., Kazantsev, I.G.: Stable convergence behavior under summable perturbations of a class of projection methods for convex feasibility and optimization problems. IEEE J. Sel. Top. Signal Process. 1(4), 540–547 (2007)
Cegielski, A.: Iterative Methods for Fixed Point Problems in Hilbert Spaces Springer (2012)
Cegielski, A., Al-Musallam, F.: Superiorization with level control. Inv. Probl. 33(4), 044009 (2017)
Censor, Y.: Weak and strong superiorization: between feasibility-seeking and minimization. Analele Universitatii Ovidius Constanta-Seria Matematica 23(3), 41–54 (2015)
Censor, Y.: Can linear superiorization be useful for linear optimization problems? Inv. Probl. 33(4), 044006 (2017)
Censor, Y., Davidi, R., Herman, G.T.: Perturbation resilience and superiorization of iterative algorithms. Inv. Probl. 26(6), 065008 (2010)
Censor, Y., Davidi, R., Herman, G.T., Schulte, R.W., Tetruashvili, L.: Projected subgradient minimization versus superiorization. J. Optim. Theory Appl. 160(3), 730–747 (2014)
Censor, Y., Elfving, T.: Block-iterative algorithms with diagonally scaled oblique projections for the linear feasibility problem. SIAM J. Matrix Anal. Appl. 24(1), 40–58 (2002)
Censor, Y., Elfving, T., Herman, G.T., Nikazad, T.: On diagonally relaxed orthogonal projection methods. SIAM J. Sci. Comput. 30(1), 473–504 (2008)
Censor, Y., Gordon, D., Gordon, R.: BICAV: an inherently parallel algorithm for sparse systems with pixel-dependent weighting. IEEE Trans. Med. Imaging 20(10), 1050–1060 (2001)
Elfving, T., Nikazad, T.: Properties of a class of block-iterative methods. Inv. Probl. 25(11), 115011 (2009)
Gordon, R., Bender, R., Herman, G.T.: Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and x-ray photography. J. Theor. Biol. 29(3), 471–481 (1970)
Hansen, P.C.: Discrete Inverse Problems: Insight and Algorithms. SIAM, Philadelphia (2010)
Hansen, P.C., Jørgensen, J.S.: AIR Tools II: algebraic iterative reconstruction methods, improved implementation. Numer. Algorithms 79(1), 107–137 (2018)
Herman, G.T.: Fundamentals of Computerized Tomography: Image Reconstruction from Projections. Springer Science & Business Media, Berlin (2009)
Herman, G.T., Garduño, E., Davidi, R., Censor, Y.: Superiorization: an optimization heuristic for medical physics. Med. Phys. 39(9), 5532–5546 (2012)
Natterer, F.: The Mathematics of Computerized Tomography. SIAM, Philadelphia (2001)
Nedic, A., Bertsekas, D.P.: Incremental subgradient methods for nondifferentiable optimization. SIAM J. Optim. 12(1), 109–138 (2001)
Neto, E.S.H., De Pierro, A.́R.: Incremental subgradients for constrained convex optimization: a unified framework and new methods. SIAM J. Optim. 20(3), 1547–1572 (2009)
Nikazad, T., Abbasi, M.: Perturbation-resilient iterative methods with an infinite pool of mappings. SIAM J. Numer. Anal. 53(1), 390–404 (2015)
Nikazad, T., Abbasi, M.: A unified treatment of some perturbed fixed point iterative methods with an infinite pool of operators. Inv. Probl. 33(4), 044002 (2017)
Nikazad, T., Abbasi, M., Elfving, T.: Error minimizing relaxation strategies in Landweber and Kaczmarz type iterations. J. Inv. Ill-posed Probl. 25 (1), 35–56 (2017)
Nikazad, T., Abbasi, M., Mirzapour, M.: Convergence of string-averaging method for a class of operators. Optim. Methods Softw. 31(6), 1189–1208 (2016)
Nikazad, T., Davidi, R., Herman, G.T.: Accelerated perturbation-resilient block-iterative projection methods with application to image reconstruction. Inv. Probl. 28(3), 035005 (2012)
Penfold, S., Schulte, R.W., Censor, Y., Rosenfeld, A. B.: Total variation superiorization schemes in proton computed tomography image reconstruction. Med. Phys. 37(11), 5887–5895 (2010)
Reem, D., De Pierro, A.: A new convergence analysis and perturbation resilience of some accelerated proximal forward–backward algorithms with errors. Inv. Probl. 33(4), 044001 (2017)
Zibetti, M.V.W., Lin, C., Herman, G.T.: Total variation superiorized conjugate gradient method for image reconstruction. Inv. Probl. 34(3), 034001 (2018)
Acknowledgements
We thank two anonymous reviewers for their detailed and constructive comments which much improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In this appendix, we provide some reasons for picking subgradient projections rather than other non-ascent directions in Algorithm 2.
Let g and Ω be a convex function and a closed convex set, respectively. Furthermore, let
and ℓ denote a subgradient of g at x. Also, assume that there exists T > 0 such that x − Tℓ ∈Ω. We show that there exists t > 0 such that d(y, C) < d(x, C) where y = x − tℓ and d is a Euclidean metric on \(\mathbb {R}^{n}.\) Based on the definition of ℓ, we get 〈z − x, ℓ〉≤ g(z) − g(x). Since z ∈ C and x ∈Ω, we get g(z) − g(x) < 0 which leads to 〈z − x, ℓ〉 < 0. Put 𝜃 = g(z) − g(x) < 0 and for t > 0 we have
Since 𝜃 < 0, we get that 2𝜃 + t∥ℓ∥2 < 0 for small enough t > 0. Therefore, we get
Since g is a convex function, we conclude that C is a convex set and consequently PC(x), the orthogonal projection of x onto C, exists. Replacing z by PC(x) in (32) leads to
Combining (33) and the fact that d(y, C) = ∥PC(y) − y∥≤∥PC(x) − y∥, we get d(y, C) < d(x, C). Note: for 0 < t ≤ T and x − Tℓ, x ∈Ω, we get y = x − tℓ = (t/T)(x − Tℓ) + (1 − t/T)x ∈Ω.
Rights and permissions
About this article
Cite this article
Nikazad, T., Abbasi, M., Afzalipour, L. et al. A new step size rule for the superiorization method and its application in computerized tomography. Numer Algor 90, 1253–1277 (2022). https://doi.org/10.1007/s11075-021-01229-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-021-01229-z
Keywords
- Convex feasibility problem
- Strictly quasi-nonexpansive operator
- Convex optimization
- Perturbation resilient iterative method
- Superiorization
- Computed tomography
- Sequential block method