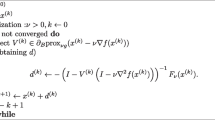Newton method for ℓ0-regularized optimization | Numerical Algorithms Skip to main content
Springer Nature Link
Log in

Newton method for ℓ0-regularized optimization

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

As a tractable approach, regularization is frequently adopted in sparse optimization. This gives rise to regularized optimization, which aims to minimize the ℓ0 norm or its continuous surrogates that characterize the sparsity. From the continuity of surrogates to the discreteness of the ℓ0 norm, the most challenging model is the ℓ0-regularized optimization. There is an impressive body of work on the development of numerical algorithms to overcome this challenge. However, most of the developed methods only ensure that either the (sub)sequence converges to a stationary point from the deterministic optimization perspective or that the distance between each iteration and any given sparse reference point is bounded by an error bound in the sense of probability. In this paper, we develop a Newton-type method for the ℓ0-regularized optimization and prove that the generated sequence converges to a stationary point globally and quadratically under the standard assumptions, theoretically explaining that our method can perform surprisingly well.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. Available at https://github.com/ShenglongZhou/NL0R

  2. http://ftp.cs.wisc.edu/math-prog/matlab/lemke.m

References

  1. Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized gauss–seidel methods. Math. Program. 137(1-2), 91–129 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bahmani, S., Raj, B., Boufounos, P.T.: Greedy sparsity constrained optimization. J. Mach. Learn. Res. 14(Mar), 807–841 (2013)

    MathSciNet  MATH  Google Scholar 

  3. Bao, C., Dong, B., Hou, L., Shen, Z., Zhang, X., Zhang, X.: Image restoration by minimizing zero norm of wavelet frame coefficients. Inv. Probl. 32(11), 115004 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  4. Beck, A., Eldar, Y.C.: Sparsity constrained nonlinear optimization: Optimality conditions and algorithms. SIAM J. Optim. 23(3), 1480–1509 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Beck, A., Hallak, N.: Proximal mapping for symmetric penalty and sparsity. SIAM J. Optim. 28(1), 496–527 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bertsimas, D., King, A., Mazumder, R.: Best subset selection via a modern optimization lens. Ann. Stat., 813–852 (2016)

  7. Bian, W., Chen, X.: Smoothing neural network for constrained non-Lipschitz optimization with applications. IEEE Transactions on Neural Networks and Learning Systems 23(3), 399–411 (2012)

    Article  MathSciNet  Google Scholar 

  8. Bian, W., Chen, X.: Linearly constrained non-Lipschitz optimization for image restoration. SIAM Journal on Imaging Sciences 8(4), 2294–2322 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bian, W., Chen, X.: A smoothing proximal gradient algorithm for nonsmooth convex regression with cardinality penalty. SIAM J. Numer. Anal. 58 (1), 858–883 (2020)

    Article  MathSciNet  Google Scholar 

  10. Blanchard, J.D., Tanner, J.: Wei, K.: CGIHT: conjugate gradient iterative hard thresholding for compressed sensing and matrix completion. Information and Inference: A Journal of the IMA 4(4), 289–327 (2015)

    MathSciNet  MATH  Google Scholar 

  11. Blumensath, T.: Accelerated iterative hard thresholding. Signal Process. 92(3), 752–756 (2012)

    Article  Google Scholar 

  12. Blumensath, T., Davies, M.E.: Gradient pursuits. IEEE Trans. Signal Process. 56(6), 2370–2382 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  13. Blumensath, T., Davies, M.E.: Iterative thresholding for sparse approximations. Journal of Fourier analysis and Applications 14(5-6), 629–654 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  14. Blumensath, T., Davies, M.E.: Normalized iterative hard thresholding: Guaranteed stability and performance. IEEE Journal of Selected Topics in Signal Processing 4(2), 298–309 (2010)

    Article  Google Scholar 

  15. Candès, E. J., Romberg, J., Tao, T.: Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52(2), 489–509 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  16. Candès, E. J., Tao, T.: Decoding by linear programming. IEEE Trans. Inf. Theory 51(12), 4203–4215 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  17. Chen, X., Ng, M.K., Zhang, C.: Non-Lipschitz ℓp-regularization and box constrained model for image restoration. IEEE Trans. Image Process. 21(12), 4709–4721 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  18. Cheng, W., Chen, Z., Hu, Q.: An active set Barzilar-Borwein algorithm for ℓ0 regularized optimization Journal of Global Optimization (2019)

  19. Cottle, R.W.: Linear complementarity problem Springer (2009)

  20. Dai, W., Milenkovic, O.: Subspace pursuit for compressive sensing signal reconstruction. IEEE transactions on Information Theory 55(5), 2230–2249 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. De Luca, T., Facchinei, F., Kanzow, C.: A semismooth equation approach to the solution of nonlinear complementarity problems. Math. Program. 75(3), 407–439 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  22. Dinh, T., Wang, B., Bertozzi, A.L., Osher, S.J., Xin, J.: Sparsity meets robustness: channel pruning for the feynman-kac formalism principled robust deep neural nets. arXiv:2003.00631 (2020)

  23. Donoho, D.L.: Compressed sensing. IEEE Trans. Inf. Theory 52 (4), 1289–1306 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  24. Elad, M.: Sparse and redundant representations: from theory to applications in signal and image processing Springer Science & Business Media (2010)

  25. Elad, M., Figueiredo, M.A., Ma, Y.: On the role of sparse and redundant representations in image processing. Proc. IEEE 98(6), 972–982 (2010)

    Article  Google Scholar 

  26. Facchinei, F.: Minimization of sc1 functions and the maratos effect. Oper. Res. Lett. 17(3), 131–138 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  27. Facchinei, F., Kanzow, C.: A nonsmooth inexact newton method for the solution of large-scale nonlinear complementarity problems. Math. Program. 76 (3), 493–512 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  28. Foucart, S.: Hard thresholding pursuit: an algorithm for compressive sensing. SIAM J. Numer. Anal. 49(6), 2543–2563 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  29. Huang, J., Jiao, Y., Liu, Y., Lu, X.: A constructive approach to l0 penalized regression. J. Mach. Learn. Res. 19(1), 403–439 (2018)

    Google Scholar 

  30. Ito, K., Kunisch, K.: A variational approach to sparsity optimization based on lagrange multiplier theory. Inv. Probl. 30(1), 015001 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  31. Jiao, Y., Jin, B., Lu, X.: A primal dual active set with continuation algorithm for the ℓ0-regularized optimization problem. Appl. Comput. Harmon. Anal. 39(3), 400–426 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  32. Lai, M.J., Xu, Y., Yin, W.: Improved iteratively reweighted least squares for unconstrained smoothed ℓq minimization. SIAM J. Numer. Anal. 51(2), 927–957 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  33. Lin, S., Ji, R., Li, Y., Deng, C., Li, X.: Toward compact convnets via structure-sparsity regularized filter pruning. IEEE Trans. Neural Netw. Learn. Syst. (2019)

  34. Lou, Y., Yan, M.: Fast l1 − l2 minimization via a proximal operator. J. Sci. Comput. 74(2), 767–785 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  35. Lu, Z.: Iterative hard thresholding methods for ℓ0 regularized convex cone programming. Math. Program. 147(1-2), 125–154 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  36. Lu, Z., Zhang, Y.: Sparse approximation via penalty decomposition methods. SIAM J. Optim. 23(4), 2448–2478 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  37. Moré, J. J., Sorensen, D.C.: Computing a trust region step. SIAM J. Sci. Stat. Comput. 4(3), 553–572 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  38. Needell, D., Tropp, J.A.: Cosamp: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 26(3), 301–321 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  39. Pan, L., Zhou, S., Xiu, N., Qi, H.D.: A convergent iterative hard thresholding for nonnegative sparsity optimization. Pacific J. Optim. 13 (2), 325–353 (2017)

    MathSciNet  MATH  Google Scholar 

  40. Pati, Y.C., Rezaiifar, R., Krishnaprasad, P.S.: Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In: Signals, Systems and Computers, 1993. 1993 Conference Record of the Twenty-Seventh Asilomar Conference on, pp 40–44. IEEE (1993)

  41. Patrascu, A., Necoara, I., Patrinos, P.: A proximal alternating minimization method for ℓ0-regularized nonlinear optimization problems: Application to state estimation. In: Proceedings of the IEEE Conference on Decision and Control, vol. 2015, pp 4254–4259 (2015)

  42. Shang, M., Zhang, C., Xiu, N.: Minimal zero norm solutions of linear complementarity problems. J. Optim. Theory Appl. 163(3), 795–814 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  43. Shang, M., Zhou, S., Xiu, N.: Extragradient thresholding methods for sparse solutions of co-coercive ncps. J. Inequal. Appl. 2015(1), 34 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  44. Soubies, E., Blanc-Féraud, L., Aubert, G.: A continuous exact ℓ0 penalty (cel0) for least squares regularized problem. SIAM J. Imaging Sci. 8(3), 1607–1639 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  45. Soussen, C., Idier, J., Duan, J., Brie, D.: Homotopy based algorithms for ℓ0-regularized least squares. IEEE Trans. Signal Process. 63(13), 3301–3316 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  46. Tropp, J.A.: Just relax: Convex programming methods for identifying sparse signals in noise. IEEE Trans. Inf. Theory 52(3), 1030–1051 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  47. Tropp, J.A., Gilbert, A.C.: Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 53(12), 4655–4666 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  48. Wright, J., Ma, Y., Mairal, J., Sapiro, G., Huang, T.S., Yan, S.: Sparse representation for computer vision and pattern recognition. Proc. IEEE 98(6), 1031–1044 (2010)

    Article  Google Scholar 

  49. Xie, J., He, S., Zhang, S.: Randomized portfolio selection with constraints. Pacific J. Optim. 4(1), 89–112 (2008)

    MathSciNet  MATH  Google Scholar 

  50. Yin, P., Lou, Y., He, Q., Xin, J.: Minimization of 1-2 for compressed sensing. SIAM J. Sci. Comput. 37(1), A536–A563 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  51. Yuan, X.T., Li, P., Zhang, T.: Gradient hard thresholding pursuit. J. Mach. Learn. Res. 18(1), 6027–6069 (2017)

    MathSciNet  MATH  Google Scholar 

  52. Yuan, X.T., Liu, Q.: Newton greedy pursuit: A quadratic approximation method for sparsity-constrained optimization. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 4122–4129 (2014)

  53. Yuan, X.T., Liu, X., Yan, S.: Visual classification with multitask joint sparse representation. IEEE Trans. Image Process. 21(10), 4349–4360 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  54. Zhou, S., Shang, M., Pan, L., Li, M.: Newton hard thresholding pursuit for sparse lcp via a new merit function. arXiv:2004.02244 (2020)

  55. Zhou, S., Xiu, N., Qi, H.D.: Global and quadratic convergence of Newton hard-thresholding pursuit. J. Mach. Learn. Res. 22(12), 1–45 (2021)

    MathSciNet  MATH  Google Scholar 

  56. Zhou, S., Xiu, N., Wang, Y., Kong, L., Qi, H.D.: A null-space-based weighted ℓ1 minimization approach to compressed sensing. Inf. Inference 5(1), 76–102 (2016)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors sincerely thank the editor and an anonymous referee for their constructive comments, which have significantly improved the quality of the paper.

Funding

This work was funded by the National Science Foundation of China (11971052, 11801325, 11771255) and Young Innovation Teams of Shandong Province (2019KJI013).

Author information

Authors and Affiliations

  1. School of Mathematics, University of Southampton, Southampton, SO17 1BJ, UK

    Shenglong Zhou

  2. Department of Mathematics and Statistics, Shandong University of Technology, Zibo, 255049, China

    Lili Pan

  3. Department of Applied Mathematics, Beijing Jiaotong University, Beijing, 100044, China

    Naihua Xiu

Authors
  1. Shenglong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lili Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Naihua Xiu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lili Pan.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, S., Pan, L. & Xiu, N. Newton method for ℓ0-regularized optimization. Numer Algor 88, 1541–1570 (2021). https://doi.org/10.1007/s11075-021-01085-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-021-01085-x

Keywords

Mathematics Subject Classification (2010)

Search

Navigation