Finite-Time Stability for Caputo–Katugampola Fractional-Order Time-Delayed Neural Networks | Neural Processing Letters Skip to main content
Springer Nature Link
Log in

Finite-Time Stability for Caputo–Katugampola Fractional-Order Time-Delayed Neural Networks

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

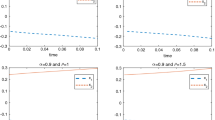
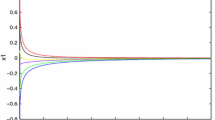
In this paper, an original scheme is presented, in order to study the finite-time stability of the equilibrium point, and to prove its existence and uniqueness, for Caputo–Katugampola fractional-order neural networks, with time delay. The proposed scheme uses a newly introduced fractional derivative concept in the literature, which is the Caputo–Katugampola fractional derivative. The effectiveness of the theoretical results is shown through simulations for two numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Price M, Glass J, Chandrakasan AP (2018) A low-power speech recognizer and voice activity detector using deep neural networks. IEEE J Solid-State Circuits 53(1):66–75

    Google Scholar 

  2. Gopinath B (2018) A benign and malignant pattern identification in cytopathological images of thyroid nodules using gabor filter and neural networks. Asian J Converg Technol. https://doi.org/10.33130/asian%20journals.v4iI.414

  3. Li Y, Tong S (2017) Adaptive neural networks decentralized FTC design for nonstrict-feedback nonlinear interconnected large-scale systems against actuator faults. IEEE Trans Neural Netw Learn Syst 28(11):2541–2554

    MathSciNet  Google Scholar 

  4. Rajchakit G (2017) Stability of control neural networks. Int J Res Sci Eng 3(6):22

    Google Scholar 

  5. Zhang XM, Han QL (2014) Global asymptotic stability analysis for delayed neural networks using a matrix-based quadratic convex approach. Neural Netw 54:57–69

    MATH  Google Scholar 

  6. Zhu Q, Cao J (2014) Mean-square exponential input-to-state stability of stochastic delayed neural networks. Neurocomputing 131:157–163

    Google Scholar 

  7. Chen X, Song Q (2013) Global stability of complex-valued neural networks with both leakage time delay and discrete time delay on time scales. Neurocomputing 121:254–264

    Google Scholar 

  8. Xu C, Chen L (2018) Effect of leakage delay on the almost periodic solutions of fuzzy cellular neural networks. J Exp Theor Artif Intell 30(6):993–1011

    Google Scholar 

  9. Xu C, Chen L, Li P (2019) Effect of proportional delays and continuously distributed leakage delays on global exponential convergence of CNNS. Asian J Control 21(5):1–8

    MathSciNet  Google Scholar 

  10. Xu C (2018) Local and global Hopf bifurcation analysis on simplified bidirectional associative memory neural networks with multiple delays. Math Comput Simul 149:69–90

    MathSciNet  Google Scholar 

  11. Xu C, Tang X, Li P (2018) Existence and global stability of almost automorphic solutions for shunting inhibitory cellular neural networks with time-varying delays in leakage terms on time scales. J Appl Anal Comput 8(4):1033–1049

    MathSciNet  Google Scholar 

  12. Xu C, Li P (2018) On anti-periodic solutions for neutral shunting inhibitory cellular neural networks with time-varying delays and D operator. Neurocomputing 275:377–382

    Google Scholar 

  13. Xu C, Li P (2018) Global exponential convergence of fuzzy cellular neural networks with leakage delays, distributed delays and proportional delays. Circuits Syst Signal Process 37(1):163–177

    MathSciNet  MATH  Google Scholar 

  14. Kamenkov G (1953) On stability of motion over a finite interval of time. J Appl Math Mech 17(2):529–540

    MathSciNet  Google Scholar 

  15. Bhat SP, Bernstein DS (1998) Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans Autom Control 43(5):678–682

    MathSciNet  MATH  Google Scholar 

  16. Wang H, Zhu Q (2015) Finite-time stabilization of high-order stochastic nonlinear systems in strict-feedback form. Automatica 54:284–291

    MathSciNet  MATH  Google Scholar 

  17. Mobayen S (2016) Finite-time stabilization of a class of chaotic systems with matched and unmatched uncertainties: an LMI approach. Complexity 21(5):14–19

    MathSciNet  Google Scholar 

  18. Lu K, Xia Y (2015) Finite-time attitude stabilization for rigid spacecraft. Int J Robust Nonlinear Control 25(1):32–51

    MathSciNet  MATH  Google Scholar 

  19. Engheta N (1996) On fractional calculus and fractional multipoles in electromagnetism. IEEE Trans Antennas Propag 44(4):554–566

    MathSciNet  MATH  Google Scholar 

  20. Laskin N (2000) Fractional market dynamics. Phys A 287(3):482–492

    MathSciNet  Google Scholar 

  21. Jmal A, Naifar O, Ben Makhlouf A, Derbel N, Hammami MA (2018) Observer-based model reference control for linear fractional-order systems. Int J Digit Signal Smart Syst 2(2):136–149

    MATH  Google Scholar 

  22. Jmal A, Naifar O, Ben Makhlouf A, Derbel N, Hammami MA (2018) Sensor fault estimation for fractional-order descriptor one-sided Lipschitz systems. Nonlinear Dyn 91(3):1713–1722

    MATH  Google Scholar 

  23. Ben Makhlouf A, Nagy AM (2018) Finite‐time stability of linear Caputo–Katugampola fractional-order time delay systems. Asian J Control. https://doi.org/10.1002/asjc.1880

  24. Kaslik E, Sivasundaram S (2012) Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw 32:245–256

    MATH  Google Scholar 

  25. Bao HB, Cao JD (2015) Projective synchronization of fractional-order memristor-based neural networks. Neural Netw 63:1–9

    MATH  Google Scholar 

  26. Thuan MV, Huong DC, Hong DT (2018) New results on robust finite-time passivity for fractional-order neural networks with uncertainties. Neural Process Lett. https://doi.org/10.1007/s11063-018-9902-9

  27. Thuan MV, Binh TN, Huong DC (2018) Finite-time guaranteed cost control of caputo fractional-order neural networks. Asian J Control 22(1):1–10

    Google Scholar 

  28. Peng X, Wu H, Song K, Shi J (2017) Global synchronization in finite time for fractional-order neural networks with discontinuous activations and time delays. Neural Netw 94:46–54

    Google Scholar 

  29. Peng X, Wu H, Cao J (2018) Global nonfragile synchronization in finite time for fractional-order discontinuous neural networks with nonlinear growth activations. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2018.2876726

  30. Peng X, Wu H (2018) Robust mittag-leffler synchronization for uncertain fractional-order discontinuous neural networks via non-fragile control strategy. Neural Process Lett 48(3):1521–1542

    Google Scholar 

  31. Liu M, Wu H (2018) Stochastic finite-time synchronization for discontinuous semi-Markovian switching neural networks with time delays and noise disturbance. Neurocomputing 310:246–264

    Google Scholar 

  32. Ran-Chao W, Xin-Dong H, Li-Ping C (2013) Finite-time stability of fractional-order neural networks with delay. Commun Theor Phys 60(2):189

    MathSciNet  MATH  Google Scholar 

  33. Alofi A, Cao J, Elaiw A, Al-Mazrooei A (2014) Delay-dependent stability criterion of Caputo fractional neural networks with distributed delay. Discret Dyn Nat Soc. https://doi.org/10.1155/2014/529358

  34. Ke Y, Miao C (2015) Stability analysis of fractional-order Cohen–Grossberg neural networks with time delay. Int J Comput Math 92(6):1102–1113

    MathSciNet  MATH  Google Scholar 

  35. Yang X, Song Q, Liu Y, Zhao Z (2015) Finite-time stability analysis of fractional-order neural networks with delay. Neurocomputing 152:19–26

    Google Scholar 

  36. Xu C, Li P (2018) On finite-time stability for fractional-order neural networks with proportional delays. Neural Process Lett. https://doi.org/10.1007/s11063-018-9917-2

  37. Katugampola UN (2011) New approach to a generalized fractional integral. Appl Math Comput 218(3):860–865

    MathSciNet  MATH  Google Scholar 

  38. Katugampola UN (2014) A new approach to generalized fractional derivatives. Bull Math Anal Appl 6(4):1–15

    MathSciNet  MATH  Google Scholar 

  39. Kilbas AA, Srivastava HH, Trujillo JJ (2006) Theory and applications of fractional differential equations. Elsevier, Amsterdam

    MATH  Google Scholar 

  40. Anderson DR, Ulness DJ (2015) Properties of the Katugampola fractional derivative with potential application in quantum mechanics. J Math Phys 56(6):063502

    MathSciNet  MATH  Google Scholar 

  41. Wu H, Zhang X, Xue S, Wang L, Wang Y (2016) LMI conditions to global Mittag–Leffler stability of fractional-order neural networks with impulses. Neurocomputing 193:148–154

    Google Scholar 

  42. Wang LF, Wu H, Liu DY, Boutat D, Chen YM (2018) Lur’e Postnikov Lyapunov functional technique to global Mittag–Leffler stability of fractional-order neural networks with piecewise constant argument. Neurocomputing 302:23–32

    Google Scholar 

  43. Kuczma M (2009) An introduction to the theory of functional equations and inequalities: Cauchy’s equation and Jensen’s inequality. Springer Science & Business Media, Berlin

    MATH  Google Scholar 

  44. Mitrinovic ND (1970) Analytic inequalities. Springer, New York

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Control and Energy Management Laboratory, National School of Engineering, Sfax University, BP 1173, 3038, Sfax, Tunisia

    Assaad Jmal & Omar Naifar

  2. Department of Mathematics, College of Science, Jouf University, Aljouf, Saudi Arabia

    Abdellatif Ben Makhlouf

  3. Department of Mathematics, Faculty of Science, Kuwait University, 13060, Safat, Kuwait

    A. M. Nagy

  4. Department of Mathematics, Faculty of Science, Benha University, Benha, 13518, Egypt

    A. M. Nagy

Authors
  1. Assaad Jmal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdellatif Ben Makhlouf
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. M. Nagy
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Omar Naifar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. M. Nagy.

Ethics declarations

Conflict of interest

The authors declare that they have no conflicts of interest.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jmal, A., Ben Makhlouf, A., Nagy, A.M. et al. Finite-Time Stability for Caputo–Katugampola Fractional-Order Time-Delayed Neural Networks. Neural Process Lett 50, 607–621 (2019). https://doi.org/10.1007/s11063-019-10060-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-019-10060-6

Keywords

Search

Navigation