Identification of Box–Jenkins models for spatially interconnected systems in closed-loop | Multidimensional Systems and Signal Processing Skip to main content
Springer Nature Link
Log in

Identification of Box–Jenkins models for spatially interconnected systems in closed-loop

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

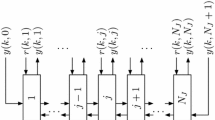
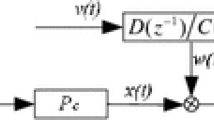
This paper presents an identification method for spatially interconnected distributed systems operating in closed-loop. The proposed approach makes use of refined instrumental variable method to identify spatially interconnected systems in Box–Jenkins form, where the controller is assumed to be known. The method presented here can yields statistically optimal estimates, and compared with other approaches to identify such systems under similar scenarios, takes far less time. The approach is applicable to both separable and non-separable systems and takes into account the boundary conditions. Though described only for two-dimensional systems, it is readily extendible to systems having more spatial dimensions. The effectiveness of the method is shown by a simulation example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Ali, M., Abbas, H., Chughtai, S., & Werner, H. (2010). Identification of spatially interconnected systems using neural networks. In Proceedings of the 49th IEEE conference on decision and control (pp. 6938–6943).

  • Ali, M., Ali, A., Abbas, H., & Werner, H. (2011a). Identification of Box–Jenkins models for parameter-varying spatially interconnected systems. In Proceedings of the American control conference, San Francisco, CA, USA.

  • Ali, M., Ali, A., Chughtai, S., & Werner, H. (2011b). Consisitent identification of spatially interconnected systems. In Proceedings of the American control conference, San Francisco, CA, USA.

  • Ali, M., Chughtai, S., & Werner, H. (2009). Identification of spatially interconnected systems. In Proceedings of the 48th IEEE conference on decision and control (pp. 7163–7168), Shanghai, China.

  • Ali, M., Popov, A., Werner, H., & Abbas, H. (2011c). Identification of distributed systems with identical subsystems. In Proceedings of the 18th IFAC world congress, Milano, Italy.

  • Arun, K., Krogmeier, J., & Potter, L. (1987). Identification of 2-D noncausal systems. In Proceedings of the IEEE conference on decision and control, Los Angeles, CA.

  • Augusta, P., Hurak, Z., & Rogers, E. (2007). An algebraic approach to the control of spatially distributed systems—The 2-D systems case with a physical application. In Proceedings of the 3rd IFAC symposium on systems, structure and control, Brazil.

  • Bamieh, B., Paganini, F., & Dahleh, M. (2002). Distributed control of spatially invariant systems. IEEE Transactions on Automatic Control, 47(7), 1091–1107.

    Article  MathSciNet  MATH  Google Scholar 

  • Banks, H., & Kunish, K. (1989). Estimation techniques for distributed parameters systems. Boston: Birkhäuser. ISBN 0817634339.

  • Bewley, T., & Liu, S. (1998). Optimal and robust control and estimation of linear paths to transition. Journal of Fluid Mechanics, 365(12), 305–349.

    Article  MathSciNet  MATH  Google Scholar 

  • Chen, C., & Kao, Y. (1979). Identification of two-dimensional transfer function from finite input-output data. IEEE Transactions on Automatic Control, 24(5), 748–752.

    Article  MATH  Google Scholar 

  • Chughtai, S., & Werner, H. (2007). Fixed structure controller design for a class of spatially interconnected systems. In Proceedings of the IFAC symposium on large scale systems, Gdansk, Poland.

  • Chughtai, S., & Werner, H. (2008a). Distributed control for a class of spatially interconnected discrete-time systems. In Proceedings of the 17th IFAC world congress (pp. 7761–7766), Seoul, South Korea.

  • Chughtai, S., & Werner, H. (2008b). New dilated LMIs to synthesize controllers for a class of spatially interconnected systems. In Proceedings of the 17th IFAC world congress (pp. 7767–7771), Seoul, South Korea.

  • D’Andrea, R. (1999) Linear matrix enequalities, multidimensional system optimization, and control of spatially distributed systems an example. In Proceedings of the American control conference (pp. 2713–2717).

  • D’Andrea, R., & Dullerud, G. E. (2003). Distributed control design for spatially interconnected systems. IEEE Transactions on Automatic Control, 48(9), 1478–1495.

    Article  MathSciNet  MATH  Google Scholar 

  • Fraanji, R., & Verhaegen, M. (2005). A spatial canonical approach to multidimensional state-space identification for distributed parameter systems. In Fourth international workshop on multidimensional systems NDS 2005, Wuppertal, Germany.

  • Gilson, M., Garnier, H., Young, P., & Van den Hof, P. (2006). A refined IV method for closed loop system identification. In Proceedings of the 14th IFAC symposium on system identification (pp. 903–908).

  • Gilson, M., Garnier, H., Young, P., &  Van den Hof, P. (2009). Refined instrumental variable methods for closed loop system identification. In Proceedings of the 15th IFAC symposium on system identification (pp. 284–289).

  • Gorinevsky, D., Boyd, S., & Stein, G. (2008). Design of low-bandwidth spatially distributed feedback. IEEE Transactions on Automatic Control, 53(1), 257–272.

    Article  MathSciNet  MATH  Google Scholar 

  • Krogmeier, J., & Arun, K. (1989). A comparative study of causal and non-causal models for multidimensional spectrum estimation. In Maple Press.

  • Lashgari, B., Silverman, L. M., & Abramatic, J. (1983). Approximation of 2-D separable in denominator filters. IEEE Transactions on Circuits and Systems, 30(2), 107–121.

    Article  MathSciNet  MATH  Google Scholar 

  • Li, P., Kruger, U., & Irwin, G. W. (2006). Identification of dynamic systems under closed-loop control. International Journal of Systems and Science, 37(3), 181–195.

    Article  MathSciNet  MATH  Google Scholar 

  • Ljung, L. (1999). System identification, theory for the user (2nd edn). USA: Prentice-Hall. ISBN 0-13-656695-2.

  • Ramos, J. (1994). A subspace algorithm for identifying 2-D separable in denominator filters. IEEE Transactions on Circuits and Systems, 41(1), 63–67.

    Article  MATH  Google Scholar 

  • Söderström, T., & Stoica, P. (1983). Instrumental variable methods for system identification. Berlin, Heidelberg, New York, Tokyo: Springer-Verlag.

  • Van den Hof, P. M., & de Callafon, R. A. (1996). Multivariable closed-loop identification: From indirect identification to dual-youla parametrization. In Proceedings of the 35th IEEE conference on decision and control.

Download references

Author information

Authors and Affiliations

  1. UET Taxila, Islamabad, Pakistan

    Ahsan Ali & Mukhtar Ali

Authors
  1. Ahsan Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mukhtar Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mukhtar Ali.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, A., Ali, M. Identification of Box–Jenkins models for spatially interconnected systems in closed-loop. Multidim Syst Sign Process 29, 245–255 (2018). https://doi.org/10.1007/s11045-016-0462-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-016-0462-8

Keywords