Applications of the discrete element method in mechanical engineering | Multibody System Dynamics
Skip to main content
Springer Nature Link
Log in

Applications of the discrete element method in mechanical engineering

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

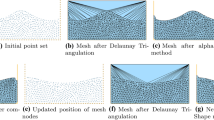
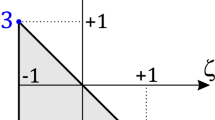
Abstract

Compared to other fields of engineering, in mechanical engineering, the Discrete Element Method (DEM) is not yet a well known method. Nevertheless, there is a variety of simulation problems where the method has obvious advantages due to its meshless nature. For problems where several free bodies can collide and break after having been largely deformed, the DEM is the method of choice. Neighborhood search and collision detection between bodies as well as the separation of large solids into smaller particles are naturally incorporated in the method. The main DEM algorithm consists of a relatively simple loop that basically contains the three substeps contact detection, force computation and integration. However, there exists a large variety of different algorithms to choose the substeps to compose the optimal method for a given problem. In this contribution, we describe the dynamics of particle systems together with appropriate numerical integration schemes and give an overview over different types of particle interactions that can be composed to adapt the method to fit to a given simulation problem. Surface triangulations are used to model complicated, non-convex bodies in contact with particle systems. The capabilities of the method are finally demonstrated by means of application examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Cundall, P.A.: A computer model for simulation of progressive, large-scale movements in blocky rock systems. In: Proceedings of the Symposium of the International Society of Rock Mechanics, Nancy (1971)

  2. Cundall, P.A., Strack, O.D.L.: A discrete numerical model for granular assemblies. Geotechnique 29, 47–56 (1979)

    Article  Google Scholar 

  3. Shabana, A.A.: Computational Dynamics. Wiley, New York (2001)

    Google Scholar 

  4. Omelyan, I.P.: On the numerical integration of motion for rigid polyatomics: the modified quaternion approach. Comput. Phys. 12(1), 97–103 (1998)

    Article  Google Scholar 

  5. Roberson, R.E., Schwertassek, R.: Dynamics of Multibody Systems. Springer, Berlin (1988)

    MATH  Google Scholar 

  6. Hairer, E., Wanner, G.: Stiff differential equations solved by Radau methods. J. Comput. Appl. Math. 111, 93–111 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  7. Hairer, E., Wanner, G.: Solving Ordinary Differential Equations. II: Stiff and Differential-Algebraic Problems. Springer, Berlin (1991)

    MATH  Google Scholar 

  8. Petzold, L.R.: A description of DASSL: a differential/algebraic system solver. In: Stepleman, R. (ed.) Scientific Computing: Application of Mathematics and Computing to the Physical Sciences, vol. 2, pp. 65–68 (1983)

  9. Verlet, L.: Computer experiments on classical fluids. Phys. Rev. 159, 98–103 (1967)

    Article  Google Scholar 

  10. Allen, M.P., Tildesley, D.J.: Computer Simulations of Liquids. Clarendon, Oxford (1989)

    Google Scholar 

  11. Geradin, M., Rixon, D.: Mechanical Vibrations. Theory and Application to Structural Dynamics. Wiley, Chichester (1997)

    Google Scholar 

  12. Zohdi, T.I.: Charge-induced clustering in multifield particulate flows. Int. J. Numer. Methods Eng. 62, 870–898 (2004)

    Article  MathSciNet  Google Scholar 

  13. Lankarani, H.M., Nikravesh, P.E.: A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 112, 369–376 (1990)

    Article  Google Scholar 

  14. Muth, B., Eberhard, P.: Collisions between particles of complex shape. In: Garcia-Rojo, R., Herrmann, H.J., McNamara, S. (eds.) Powders and Grains, pp. 1379–1383 (2005)

  15. Muth, B., Eberhard, P.: Investigation of large systems consisting of many spatial polyhedral bodies. In: van Campen, D.H., Lzurko, M.D., van den Oever, W.P.J.M. (eds.) Proceedings of the ENOC-2005, Fifth EUROMECH Nonlinear Dynamics Conference, pp. 1644–1650 (2005)

  16. Brendel, L., Dippel, S.: Lasting Contacts in Molecular Dynamics Simulations, p. 313ff. Kluwer Academic, Dordrecht (1998)

    Google Scholar 

  17. Herrmann, H., D’Adetta, G.A., Kun, F., Ramm, E.: Two-dimensional dynamic simulation of fracture and fragmentation of solids. Comput. Assis. Mech. Eng. Sci. 6, 385–402 (1999)

    MATH  Google Scholar 

  18. Potapov, A.V., Hopkins, M.A., Campbell, C.S.: A two-dimensional dynamic simulation of solid fracture. Int. J. Mod. Phys. C 6(3), 371–398 (1995)

    Article  Google Scholar 

  19. D’Addetta, G.A., Ramm, E.: A microstructure-based simulation environment on the basis of an interface enhanced particle model. Granul. Matter 8, 159–174 (2006)

    Article  Google Scholar 

  20. Liu, K., Gao, L., Tanimura, S.: Application of discrete element method in impact problems. JSME Int. J. Ser. A 47(2), 138–145 (2004)

    Article  Google Scholar 

  21. Courant, R., Friedrichs, K., Lewy, H.: On the partial difference equations of mathematical physics. IBM J. 11, 215–234 (1967)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Engineering and Computational Mechanics, University of Stuttgart, Pfaffenwaldring 9, 70569, Stuttgart, Germany

    Florian Fleissner, Timo Gaugele & Peter Eberhard

Authors
  1. Florian Fleissner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Timo Gaugele
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peter Eberhard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Florian Fleissner.

Additional information

Commemorative Contribution.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fleissner, F., Gaugele, T. & Eberhard, P. Applications of the discrete element method in mechanical engineering. Multibody Syst Dyn 18, 81–94 (2007). https://doi.org/10.1007/s11044-007-9066-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-007-9066-2

Keywords

Search

Navigation