1 Introduction

The ear is a susceptible organ of the human body. One of its primary functions is to use hearing by detecting, transmitting, and converting sounds. Another significant function of the ear is to maintain a sense of balance in our bodies. Like vision, hearing is one of our most important sources of biological information [25, 49].

Anatomically, the ear can be divided into three discriminable parts: the inner, middle, and outer ear. It includes a chain by the malleus, incus, and stapes, collectively called the auditory ossicles. It is a complex system of fluid-filled channels and cavities located deep in the hard, rocky part of the temporal bone [3, 28].

Middle ear diseases (MEDs), with the high incidence, described as lesions in the middle ear, which play a vital role in otorhinolaryngology clinical practice [10, 42]. It is the primary reason for hearing loss in many developing countries around the world [18, 34], and chronic suppurative otitis media (CSOM) and middle ear cholesteatoma (MEC) are two common types seen in clinical practice. Both of them seriously affect the patients’ quality of life and increase the burden of life [9, 29, 47]. Early diagnosis and effective treatment are the clinical goals of Otolaryngologists at present.

Otitis media (OM) is an inflammatory disease that affects all or part of the middle ear. That can also occur in the middle ear but does not usually damage the surrounding bony structures, presenting a filling phenomenon in CT scans [41]. In this paper, we mainly focus on chronic suppurative otitis media (CSOM), the most common type of otitis media, characterized by persistent repeated inflammation and complications of the tympanum or mastoid cavity [2, 8, 27]. In the CT images, the middle ear structure of patients with CSOM is relatively complete, but there are still some fillers can be found in the tympanic and mastoid cavity [30, 45].

Middle ear cholesteatoma (MEC), an uncontrolled expanding growth of the epithelium tissues surrounded by an inflammatory reaction, is another common type of middle ear disease. Although these lesions are benign, they can erode the normal bone structure of temporal bone and cause various complications. For example, damage to the auditory ossicle chain can lead to conducted hearing loss (HL). In addition, the erosion of semicircular fistulas and facial neural tubes may lead to disorders of the balance function and facial paralysis, respectively [13, 14, 19, 38]. High-resolution CT provides excellent detail in detecting cholesteatoma in the middle ear [23, 26]. From CT images, the middle ear bone structure of patients with cholesteatoma is usually partially eroded, and the surface of eroded bone is relatively smooth [40].

In recent studies, some researchers have conducted retrospective studies of patients at the BC Children’s Hospital Microtia Clinic from Jan.1, 1990 to Apr.17, 2017 to examine existing imaging and clinical records to determine the presence or nonexistence of middle ear cholesteatoma [31]. Recently, there has developed a new consensus statement on the definition and classification of middle ear cholesteatoma [5].

In clinical practice, the symptoms and results of the objective examination characteristics of MEC and CSOM are similar. MEC is often not detected or even misdiagnosed at the early stage, especially when combined with inflammation. Due to differences in pathological changes, lesion manifestations, and complications between these two diseases, achieving accurate diagnostic discrimination is crucial in clinical practice. Therapy for MEC is usually surgical intervention as early as possible. In contrast, CSOM can be treated conservatively in most cases [32], which may avoid unnecessary injuries and improve recovery efficiency to a great extent.

Previous studies have used deep learning to classify and diagnose MEDs, or other otolaryngology diseases. The most recent research indicates that using CNNs in endoscopic examinations to automate the diagnosis of ear disease and detect of tympanic membrane perforations and middle ear infection can achieve excellent precision [6, 15, 20, 52, 53, 57]. Yan-Mei Wang et al. proposed a deep learning framework for the diagnosing of CSOM based on CT scans, and the model’s performance was shown to be superior to that of clinical experts in some cases [51]. Wang et al. presented a deep-learning method for the diagnosis of CSOM and MEC, which chose Visual Geometry Group 16 (VGG-16) as the model’s backbone [55]. Moreover, Wang et al. fused individual features from both CNN and GCN to assist radiologists in rapidly detecting COVID-19 from chest CT images [54]. Parvaze et al. extracting crafted features to analyze and identification the pathologies features of peritumoral vasogenic edema [35, 36].

Comparatively, graph neural networks (GNNs) [7, 16, 22, 48] is a promising technology and emerging network architecture, which can efficiently deal with graph structure data by modeling relations between sample nodes (or vertices). In these variants of the GNN model, the graph isomorphism network (GIN) [58] has the greatest ability to represent from different graph structures and has quantifiable generalization ability, which quickly attracted wide attention from the GNN community. This special graph structural information shows some meaningful structural patterns. Because the symptoms and results of objective features of MEC and CSOM are very similar, and MEC is often not found or even misdiagnosed at an early stage, therefore, accurate diagnosis and differential diagnosis of these two diseases in clinical practice are of great significance. However, most of the previous studies used deep learning to classify and diagnose meds, but the structural features of the middle ear were not analyzed. In this work, our goal is to enhance the GIN toward better structural modeling and middle ear disease property identification via using special structural information. Moreover, our OMCNIC achieved a better classification result than [51, 55], and we analyze the effects with different parts of the middle ear structure on CSOM and MEC. We provide several middle ear examples of CSOM, MEC and normal structure in Fig. 1.

Fig. 1
figure 1

Illustration of 3 classes of ME patch examples

Full size image

To reduce the workload of radiologists and improve their work efficiency, in this paper, we proposed the first work that uses a graph isomorphism network method to evaluate the impact of structure-constrained deep feature fusion with the middle ear on chronic suppurative otitis media and cholesteatoma with CT images. The experimental results indicate the validity of our algorithm. The major contributions of this work are summarized as follows:

  • We first automatically crop the region of interest (ROI) from CT images, i.e., ME patches.

  • Based on the image patches, we use structure-constrained deep feature fusion to represent the middle ear structure and convert the middle ear structure image into a graph.

  • We use the graph isomorphism network to identify ME disease and evaluate the impact of different structures with the middle ear diseases efficiently.

  • By analyzing the effects of different structures in the middle ear on cholesteatoma and chronic suppurative otitis media, this approach can provide a new direction for preoperative and postoperative care for cholesteatoma surgery.

The rest of the contents of this paper are as follows: Part II gives the data description and preprocessing details. Part III will present our GIN model to classify chronic suppurative otitis media, cholesteatoma and normal (CSOMCN) diseases. Part IV gives our experimental results. Part V is the discussion, and Part VI is the conclusion.

2 Data description and preprocessing

The medical research and ethics committee of Xiangya Hospital, Central South University approved this study. The researchers collected these data from 573 patients who underwent middle ear surgeries in the Department of Otorhinolaryngology, Xiangya Hospital, from Jan. 2018 to Oct. 2020, the age range of patients was 5–72 years, with a mean ± SD of 38.75 ± 14.38 years. They then reviewed medical records to exclude any patient diagnosed with a congenital malformation or any postoperative situation.

Each enrolled patient at least had received one temporal bone CT scans, resulting in a total of more than 573 scans available for this study. These scans were obtained by a 256-channel multidetector Revolution CT scanner (GE Healthcare). The parameters of CT scanning were: tube voltage of 100 kV, tube current of 325mAs, pitch coefficient of 0.6875, matrix size of 512 × 512, field of view of 220 × 220 mm, thickness of layer of 0.625 mm. Body position was the standard cranial-anteriorly, scanning mode was spiral scanning, window width was 3000 ~ 4000 HU and window position was 300 ~ 500 HU.

Based on cooperation with Xiangya Hospital, the dataset that we finally adopted consists of 499 patients. Our final dataset consists of 998 unilateral ears, including 108 cases of middle ear cholesteatoma (MEC) (46 in the left ear and 62 in the right ear), 622 cases of CSOM (314 in the left and 308 in the right) and 268 cases of normal ME (139 in the left and 129 in the right), and each of cases was classified and labeled by professionals. All data were obtained with informed consent signed by the subjects. The training labels of the ROI network were annotated by an otolaryngologist. Inspired by the main ideas of Neural Style Transfer proposed by the researchers Garg [11, 46], by combining with the specificity and scarcity of our middle ear MEC data, we reused MEC data, and adding inverted left ear MEC case data to the training of the right ear pathology classifier.

Our dataset is divided into a training set, a verification set and a test set in proportions of 80%, 10% and 10%. By working together with the hospital on artificial intelligence and medical data, we obtained the hospital’s medical data and needed to preprocess the CT scans. To achieve better training results, we systematically labeled the original data under the guidance of a specialist in otolaryngology. We chose to cover the middle ear structure and crop the middle ear structure and then used it to create the ROI label to better train our classification network and to analyze the correlation between different middle ear structures. Figure 2 is an example of data preprocessing of CSOMCN on the left and right ears.

Fig. 2
figure 2

Preprocessing examples of the OMCN image

Full size image

2.1 Region of interest search net

In our experiment, we wanted our GIN algorithm to focus on the ME region in the CT image by ignoring as much other noise as possible, so we tried to build a network of regions of interest (ROIs) to extract important parts of the ME. Only in this way can we verify the accuracy and effectiveness of our OMCNIC. In addition, in order to improve accuracy and increase credibility, a professional otolaryngologist defined the “window of interest” that we need to select. Therefore, we used U-net [39] to help automatically choose bounding boxes. The U-Net network adopts a U-shaped structure with an encoder-decoder structure, which transmits low-layer feature information to the higher layer through cross-layer connection, avoiding information loss and improving segmentation accuracy. In addition, the U-Net network can maintain feature richness by increasing the number of convolution kernels and reducing the step size of pooling. These features are ideal for the region of interest extraction of medical images such as CT images. At the same time, due to the similarity of CT image density and noise interference of MEC and CSOM, it is very challenging to segment and extract ROI from ME images, and it is necessary to select a verified deep learning network to ensure accuracy and robustness. U-Net is widely used in the field of medical imaging and has achieved excellent performance in a number of medical image segmentation tasks, which can handle the challenges encountered in medical image segmentation and ROI extraction tasks very well [43]. Therefore, by analyzing the specificity of the MED image and verifying the analysis experimentally, the selection of U-Net to extract the region of interest of the ME image can ensure the accuracy and robustness of ME patches. So, we first approximately determine the ME structure through U-net’s search network. Then, we analyzed the advantages and disadvantages of various interpolation methods and the characteristics of the lesion area of our ME patches, and found that bilinear interpolation is more suitable for stabilizing the image clarity and border accuracy of the ME patches, so we use bilinear interpolation of ROI-Align to deal with the misalignment problem in U-net. Finally, we obtained a fixed-size feature map and the correct bounding box. Based on this, we were able to extract the corresponding ME patch for each patient’s CT image.

In Fig. 2, we choose the special ME patches to represent all structures of the ME. In the first stage, we use U-net to obtain the ROI image, and our goal in this phase refers to image segmentation tasks [39]; we give the loss function of our ROI search net in the following formula (Eq. 1):

$$\genfrac{}{}{0pt}{}{\begin{array}{c}E=\sum_{x\in \Omega}\omega (x)\log \left({p}_{\tau (x)}(x)\right)\ \end{array}}{\begin{array}{c}\ \\ {}\omega (x)={w}_c(x)+{\omega}_0\bullet \exp \left(-\frac{{\left({d}_1(x)+{d}_2(x)\right)}^2}{2{\sigma}^2}\right)\end{array}}$$
(1)

The energy function is calculated by the following Eq. 1, where τ : Ω → {1, …, K} is the true label of each pixel and \(\omega :\Omega \mathfrak{\to}\mathfrak{R}\) is a weight map. The separation boundary is calculated by using morphological operations, where \({\omega}_c:\Omega \mathfrak{\to}\mathfrak{R}\) is the weight map to balance the class frequencies, \({d}_1:\Omega \mathfrak{\to}\mathfrak{R}\)denotes the distance to the border of the nearest pixel and \({d}_2:\Omega \mathfrak{\to}\mathfrak{R}\) the distance to the border of the second nearest pixel. The ROI search net could divided into these steps: firstly, according to the input CT training data and proportionally divide them into training and validation sets, then do the sample mini-batch of data pairs to iterative, and then using Adam as the optimizer and using Eq. 1 as the loss function and via gradient descent to update parameters, finally we obtain the best trained model that we need.

3 Methodology

In the overall framework design of this work, we can divide it into three parts. Firstly, we collect and collate MED datasets from Department of Otorhinolaryngology of Xiangya Hospital, and do a certain preprocessing, reused MEC data and conduct data augmentation operations, and complete the fine data labeling work with the assistance of Xiangya Otorhinolaryngology experts. Then, we use the U-net algorithm to search ME patches to obtain the ROI, and then we use structure-constrained deep feature fusion to represent the middle ear structure and convert the middle ear structure image into a graph. At last, in order to make better use of the structure-constrained ME patches feature, the framework uses Graph Isomorphism Network (GIN) network to identify ME disease and evaluate the impact of different structures with the middle ear diseases efficiently.

Fig. 3
figure 3

Illustration of structure-constrained deep feature fusion of the graph

Full size image

3.1 Structure-constrained deep feature fusion

Image fusion technology has great application value in remote sensing detection, medical image analysis and clear image reconstruction, especially in computer vision [1]. In general, image fusion is divided into pixel-level image fusion, feature-level image fusion and decision-level image fusion [44]. Inspired by the idea of image feature level fusion, we extract the MEC and CSOM feature information from the source ME image, then, the fused image features are obtained by analyzing, processing and integrating the feature information. Therefore, we define an undirected graph G:= (V, E) to represent the structure of the ME, where V denotes as a set of vertices and E = {((u, v) | u, v ∈ V)} denotes as a set of edges. In this approach, we aim to cluster information from patches. For this purpose, we construct an ME graph for each patch image Pi in the dataset. In order to reduce the complexity of construction, we first resize the ME patch into a size of 100*100 and then construct an undirected graph across the smaller patches. Then, we construct different nodes by extracting the homogeneous intensity in the ME patch as the vertices of the undirected graph G and prune vertices outside the mask. And then, we calculate the correlation distance between the two vertices as the weight of the corresponding edge by Eq. 2:

$${\displaystyle \begin{array}{c}\omega =1-\frac{\left(u-\overline{u}\right)\cdot \left(v-\overline{v}\right)}{\parallel \left(u-\overline{u}\right){\parallel}_2\parallel \left(v-\overline{v}\right){\parallel}_2}\in \mathcal{W}\end{array}}$$
(2)

We take the pixel value of the corresponding vertex on the patch as the attribute value of the vertex on the undirected graph G. The coordinates and intensity are formed as the attribute value by using a k-nearest neighbor adjacency matrix with Eq. 3:

$${\displaystyle \begin{array}{c}{f}_{i,j}\to {a}_{i,j}=\exp \left(-\frac{{\parallel {x}_i-{x}_j\parallel}^2}{\sigma_x^2}\right)\in \mathcal{A}\end{array}}$$
(3)

where vectors xi and xj are the spectral signatures associated with the vertices vi and vj, and σx is the scale parameter defined as the average coordinate distance xk of the k-nearest neighbors (e.g., k = 8) for each vertex. Let Ej as a set of edges in vj, then we let rj as the feature vector of Ej and we define rj as Eq. 4:

$${\displaystyle \begin{array}{c}{r}_j=\phi \left(\sum\limits_{e_{i,j}\in {E}_j}\kern0.1em {f}_{i,j}\right)\in \mathcal{R}\end{array}}$$
(4)

where ϕ is a linear transform function. fi, j is the feature vector of its neighborhoods ei, j with the vertices vi and vj. Once \(\mathcal{A}\) is given, we can construct the graph Laplacian matrix \({\mathcal{L}}^{\prime }\) as following Eq. 5:

$${\displaystyle \begin{array}{c}\begin{array}{c}\mathcal{L}=\mathcal{D}-\mathcal{A}\\ {}\mathcal{D}=\sum\limits_j\kern0.1em {A}_{i,j}\\ {}{\mathcal{L}}^{\prime }={\mathcal{D}}^{\frac{1}{2}}{\mathcal{L}\mathcal{D}}^{\frac{1}{2}}\\ {}=I-{\mathcal{D}}^{\frac{1}{2}}\mathcal{A}{\mathcal{D}}^{\frac{1}{2}}\end{array}\end{array}}$$
(5)

where Ι is the identity matrix. The resultant graphs are of sizes 30–100 nodes for an ME patch, we found that our GIN with 75 nodes has achieved the best entire average classification results. The construction detail of the ME graph is given in Alg. 1. Using the proposed structure-constrained deep feature fusion, each ME graph is obtained and is represented in its structure-aware representation.

Figure 3 presents visualization of the structure-constrained deep feature fusion graphs, which indicate the graph representation (i.e., node, coordinate and feature of the node) of MEC. From the ‘node’ column of Fig. 3, the middle ear bone structure of patients with cholesteatoma is incomplete, the sinus opening in the tympanic membrane is enlarged, and the surrounding bone layer is thinner. From the ‘with coord’ column of Fig. 3, we can find that the corresponding location of tympanic node is very sparse, that is, the mastoid process of the middle ear is destroyed. According to the ‘feat and coord’ column of Fig. 3, we can observe that the relation between these nodes is that the more edges there are between two nodes, the closer their relationship.

Algorithm 1
figure a

Strategy of Structure-Constrained Deep Feature Fusion

Full size image

3.2 OMCNIC algorithm

The graph Isomorphic Network (GIN) [58] is a classic variant of GNN with great potential, and it has a discriminative power that is equal to that of Weisfeiler-Lehman (WL) graph isomorphism test power [4, 56]. The GIN could iterate the node information by the following Eq. 6:

$${\displaystyle \begin{array}{c}{h}_i^{k+1}= ML{P}^k\left(\left(1+{\xi}^k\right){h}_i^k+\sum\limits_{j\in {N}_i}\kern0.1em {h}_j^k\right)\end{array}}$$
(6)

we set \({h}_i^0={\mathcal{A}}_i\), ξk is a parameter that can be improved by learning and MLP is a multilayer perceptron. Moreover, GIN concatenates the information represented by the nodes on all layers of the model according to the Eq. 7 to obtain the final representation:

$${\displaystyle \begin{array}{c}{h}_G=\textrm{CONCAT}\left(\sum\limits_{v\in G,k=0}^K\kern0.1em {h}_v^k\right)\end{array}}$$
(7)

we set v and G represent as the node and the corresponding graph, respectively. we set COCATN(∙) as the concatenate function. It has been proved from experimentally that the GIN has a more powerful representational power of graph structures than other GNN variant models.

Chronic otitis media and cholesteatoma classification can be regarded as a multiclass identification problem of ME structural graphs in artificial intelligence, which can be denoted as follows: we first given a set of structural graphs G = {G1, G2, ⋯, Gn} and their label set Y = {y1, y2, ⋯, ym}, each structural graph Gi has an attribute vector of vertices \(\left(r\in \mathcal{A}\right)\) and a feature vector of edges \(\left(r\in \mathcal{R}\right)\). Furthermore, we set σ(∙) to represent the learning function which could learns the corresponding vector \({h}_G=\sigma \left(\mathcal{A},\mathcal{R}\right)\) to aid to predict the labels. At last, we let the labeling function ζ(∙) to allocates the label of the entire structural graph y = ζ(hG).

We have improved the ability of GIN to represent the structure graph by two solutions: vertex feature cascading and neighborhood weight changes with using a gate unit. We concatenate rj (from Eq. 4) to the neighbor’s feature vector of the central vertex hj on every layer of the GIN clustering. Therefore, the Eq. 6 could be replaced by the following formulation Eq. 8.

$${\displaystyle \begin{array}{c}{h}_i^{k+1}= ML{P}^k\left(\left(1+{\xi}^k\right){h}_i^k+\sum\limits_{j\in {N}_i}\kern0.1em \left({h}_j^k\oplus {r}_j^k\right)\right)\end{array}}$$
(8)

Where ⊕ set as the concatenation. Moreover, Eq. 7 can be replaced by the following Eq. 9:

$${\displaystyle \begin{array}{c}{h}_G= CONCAT\left(\sum\limits_{i\in V,k=0}^K\kern0.1em {h}_i^k\oplus {r}_i^k\right)\end{array}}$$
(9)

Therefore, the enhance GIN algorithm that we presented can cluster the information of the vertex neighbors and made these patterns change into hidden vectors. In the GIN, all neighbors make the same contribution to vertices updates, which results in ignoring the difference in intensity of impact between the central node and its different neighbors. To solve this problem, we introduced a control gate unit to regulating the role of neighbors in updating the characteristics of the central node [12, 37]. Hence, Eq. 8 can be redefined as the following Eq. 10:

$${\displaystyle \begin{array}{c}{h}_i^{k+1}= ML{P}^k\left(\left(1+{\xi}^k\right){h}_i^k+\sum\limits_{j\in {N}_i}\kern0.1em \left(\vartheta \left({h}_j^k{\mathcal{W}}^k+{b}^k\right)\otimes {h}_j^k\oplus {r}_j^k\right)\right)\end{array}}$$
(10)

Where ⊗ is elementwise multiplication, we set \({\mathcal{W}}\;^k\) (Eq. 2) and bk represent as the weight matrix and bias of the k-th layer, respectively. By this way, acts as an adjustable, changeable controller for neighborhood weights, which learns the weight matrix to adjust the different intensity of impact between the central node and its neighbors during the training phase. Figure 4 and Alg. 2 outline the main steps of our proposed OMCNIC.

Algorithm 2
figure b

Our proposed Graph Isomorphism Network (OMCNIC)

Full size image

4 Experimental results

The proposed OMCNIC framework is used to perform the training on a ASUS 8460-PLUS server (hexa-core 2.90 GHz processor, 64 GB RAM and one NVIDIA GeForce RTX 2070 SUPER video card). The presented methods were implemented in Python using the Pytorch framework.

Fig. 4
figure 4

Illustration of structure-constrained deep feature fusion of the graph

Full size image

4.1 Performance evaluation method

In this paper, we use accuracy (ACC), sensitivity (Sens) and specificity (Spec) as our evaluation metrics. According to the classification of all test samples, the classification results of the experiment can be divided into true positive \(\left({\mathcal{M}}_{tp}\right)\), false positive \(\left({\mathcal{M}}_{fp}\right)\), true negative \(\left({\mathcal{M}}_{tn}\right)\) and false negative \(\left({\mathcal{M}}_{fn}\right)\). The three evaluation indicators are defined as follows:

$$Acc=\frac{{\mathcal{M}}_{tp}+{\mathcal{M}}_{tn}}{{\mathcal{M}}_{tp}+{\mathcal{M}}_{fp}+{\mathcal{M}}_{tn}+{\mathcal{M}}_{fn}}$$
(11a)
$$Sensitivity=\frac{{\mathcal{M}}_{tp}}{{\mathcal{M}}_{tp}+{\mathcal{M}}_{fn}}$$
(11b)
$$Specificity=\frac{{\mathcal{M}}_{tn}}{{\mathcal{M}}_{fp}+{\mathcal{M}}_{tn}}$$
(11c)

Obviously, the sensitivity refers to the proportion of positive values we predict among all the original label is positive, while the specificity refers to the proportion of negative values we predict among all the original label is negative. The accuracy (ACC) reflects the accuracy of the overall judgment of the classification model.

4.2 Hyperparameter setting

The presented and mentioned networks are trained by the Adam optimizer [21]. The primary idea of Adam’s algorithm is to computing the update step size of the parameters. The main idea of the Adam algorithm is used to calculate the updated step of the parameters. The method can automatic adjustment of the parameters of the learning rate, has little memory requirements so greatly improved the speed of training, improved stability, and thus it is suitable as the optimizer of the multi-classification problem. The Adam method is also applicable to non-stationary targets and problems with very noisy or sparse gradients, and the algorithm has stable convergence in theory [21]. Therefore, by analyzing the specificity and sparsity of our ME data and performing experimental validation, we found that the algorithm of stable and efficient Adam is suitable for our MED identification and classification problems. The form of Adam (Eq. 12) is derived as follows:

$${\displaystyle \begin{array}{c}\genfrac{}{}{0pt}{}{\alpha_t=\alpha \bullet \sqrt{1-{\beta}_2^t}/\left(1-{\beta}_1^t\right)}{\theta_t\leftarrow {\theta}_{t-1}-{\alpha}_t\bullet {m}_t/\left(\sqrt{v_t}+\hat{\epsilon}\right)}\end{array}}$$
(12)

where α is the learning rate with the default set as 0.001, mt and vt are the mean and variance of the gradient after deviation correction, respectively, and the parameter β1, β2 ∈ [0, 1), \(\hat{\epsilon}\) default is set as 10−8 to prevent a divisor of 0. More details about the setting of each parameter value in Adam hyperparameters, the underlying mathematical mechanism and the proof of convergence can be studied in detail in [21].

Rectified linear unit (ReLU) is constant at partial gradients greater than 0, there is no gradient dispersion, and the derivative of ReLU is calculated faster. The derivative of ReLU in the negative half region is 0, so when the activation value of neurons is negative, the gradient is 0, this neuron does not participate in training and has sparsity. Therefore, by analyzing the specificity of ME data and validating it experimentally, in the intermediate process of convolution, we choose the rectified linear unit (ReLU) as our activation function [50]. The form of the ReLU (Eq. 13) is derived as follows:

$${\displaystyle \begin{array}{c} ReLU(t)=\left\{\begin{array}{c}t,\kern1.5em if\kern0.75em t>0\\ {}0,\kern1.5em if\kern0.75em t\le 0\end{array}\right.\end{array}}$$
(13)

The most obvious feature of the Softmax function is that it takes the ratio of the input of each neuron to the sum of all the inputs of the current layer as the output of that neuron; that is, the greater the output of the neuron, the higher the corresponding category of the neuron is more likely to be a true category. At the same time, Softmax has the advantages of monotonicity and non-locality, which can solve the problem of slow learning and so on [17, 24]. Moreover, the training effect of Softmax with a log-likelihood cost function is better than that with a quadratic cost function, and more details of the mathematical form to prove the effectiveness of Softmax can be seen in [33]. Therefore, in the final fine-tuning of the fully connected layer, we use the Softmax function as an activation function. Then, it outputs a probability distribution for the six classes: “MEC left”, “MEC right”, “CSOM Left”, “CSOM right”, “normal left” and “normal right”. The form of the Softmax (Eq. 14) is derived as follows:

$${\displaystyle \begin{array}{c}{S}_i=\frac{e^{a_i}}{\sum_{j=1}^C{e}^{a_j}}\end{array}}$$
(14)

In the actual test model, when the sample image passes through the Softmax layer, it will take the maximum index in the vector as the prediction label of this sample. Using the cross-entropy loss function, when the error is large, the gradient is also large, the decline is faster; if the error is small, the update is slower; at the same time, the activation function in some cases into the saturation region, the gradient disappeared problem, and more details of the mathematical form to prove the effectiveness of cross-entropy loss function can be seen in [33]. So, by analyzing the characteristics of our classification problems and combining the previous Softmax [17, 24], we choose the categorical form as our loss function, the form of which (Eq. 15) is derived as follows:

$${\displaystyle \begin{array}{c} Loss=-\sum\limits_{j=1}^{outputsize}{y}_j\mathit{\log}{\hat{y}}_j\end{array}}$$
(15)

Where \({\hat{y}}_j\) is the output value and yj is the ground truth. For fairness and convenience, in this study, OMCNIC and other compared methods use the same hyperparameter settings as follows. Batch normalization was applied, the Adam optimizer with an initial learning rate of 0.001 and a learning rate delay of 0.5 per every 10 epochs were applied. Additionally, the following settings were used: the number of hidden units ∈ {8, 16, 32, 64}, the dropout ratio ∈ {0, 0.3, 0.5} and the batch size ∈ {8, 16, 32}.

4.3 Effect of structure-constrained deep feature fusion

Based on previous work, our OMCNIC has achieved good classification results. As listed in Table 1, ‘Category’ indicates the entire six categories composed of chronic suppurative otitis media, middle ear cholesteatoma and normal, ‘coor’ indicates the coordinate distance of vertices and ‘Feat’ indicates the feature vector of vertices that our GIN algorithm adopted. The experimental results indicate that the OMCNIC algorithm with the coordinate distance and feature vector achieve the best overall classification results, yielding an average accuracy, sensitivity and specificity on the actual test set of 96.36%, 99.00%, and 89.68%, respectively. In the validation set, the Val accuracy, Val sensitivity and Val specificity are 80.81%, 91.87%, and 93.57%, respectively. When the feature vector concatenation was removed, in terms of accuracy and specificity on the training dataset, OMCNIC performance was reduced by 2.88% and 4.24%, respectively, but still improved by 1.8% and 0.96% compared with GIN, respectively. When the coordinate weight adjustment was removed, in terms of accuracy and specificity on training datasets, OMCNIC performance was reduced by 1.66% and 2.01%, respectively, but still improved by 3.02% and 3.19%, respectively, compared with GIN.

Table 1 Our OMCNIC Classification Result
Full size table

In particular, our OMCNIC obtained dramatically better performance than previous GIN, increasing the performance by 4.68% on accuracy, 8.56% on sensitivity and 5.2% on specificity. This shows the effectiveness of our OMCNIC in taking the structural coordinate distance and feature vector influence between GIN-based vertices and their neighbors. As shown in Table 1, when we remove feature vector concentration or coordinate distance adjustment from the OMCNIC framework, the overall accuracy of OMCNIC decreases, but is still outperformed to GIN. The experimental results clearly support that the structural characteristics, i.e., the feature vector and coordinate distance, which could efficiently make the GNN learning more local structural features of the middle ear, hence boosting the identification of structural ME properties.

We demonstrate the confusion matrix of the testing results in Fig. 5a. The confusion matrix provides a more complete display of the performance of our algorithm. On the one hand, by testing the performance of our algorithm with structure-constrained deep feature fusion, we found that our OMCNIC achieved the best entire average classification results. On the other hand, by comparing the results from Fig. 5a, we can find that the classification accuracy of MEC and CSOM is overall higher than that of normal cases, that is primary owing to the following reasons. First of all, due to the unbalance distribution of the datasets, the pathological details of some middle ear structures of normal and chronic suppurative otitis media cannot be learned well. In contrast, the middle ear structure of middle ear cholesteatoma in the middle is well illustrated by the nodes graph, so it can be learned well by the computer implementation. Therefore, based on the goal of no missed diagnosis, we give a biased mechanism in the classification process that actually made a low accuracy in normal classes. As shown in Fig. 5b, we demonstrate the ROC result of our proposed algorithm.

Fig. 5
figure 5

The testing performance of our OMCNIC. a Confusion Matrix. b ROC curve

Full size image

4.4 Comparison with baseline models

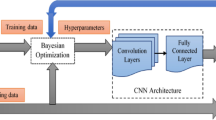
We evaluated the efficiency of our proposed algorithm for constructing the GNN to learn the structural representation for the middle ear, developing comparisons with VGG-16, InceptionV3, the graph convolutional network (GCN [22]) and the graph attention network (GAT [48]). We used accuracy for disease identification of the middle ear to evaluate and compare the performance differences between our model and the baseline model. Figure 6 shows the accuracy in the testing dataset of the comparative models on the identification of disorders of the middle ear. All in all, the overall performance of our OMCNIC is significantly better than other SOTA models. Therefore, OMCNIC is a formidable alternative framework for structural middle ear disease identification.

Fig. 6
figure 6

Comparison of accuracy results in tests of different models on ME patches

Full size image

As shown in Fig. 6, VGG-16 and InceptionV3 (the first two rows) perform the worst. It is not surprising because they are the models that have access to spatial representations. Their disappointing performance empirically supports the necessity of spatial dependencies for middle ear identification. Since the other two GNN models are enabled to capture neighboring information, we then compare them to find which method utilizes structure knowledge more effectively, most of the classification results are better than the former two models. Consequently, OMCNIC achieves moderate improvement increments of at least 0.90% with CSOM Left and at most 16.70% with Normal Right over the other two GNN model CSOMCN classification accuracy results, respectively; because the structural relation between ME patches can be excellent modeled as a graph by the GIN. As expected, the OMCNIC outperforms those comparative models, showing its ability to blend the representations of different graph structures.

As shown in Table 2, Inception-V3 [51] performed worst in accuracy and recall measures, while VGG-16 [55] performed worst in Precision and F1-score measures; we found that, compared with other methods, our OMCNIC model is only slightly inferior to the other models in specificity indicators, the other indicators have reached state of the art (SOTA) superior to the other two models. In addition, due to the very similar pathological characteristics of CSOM and MEC and the imbalance between these two types of data, partial symptoms are not evident, and the fact that both CSOM and MEC are prone to misdiagnosis, which leads to a greater number of false positives; low specificity is then obtained. Their disappointing performance in the first two CNN models empirically demonstrates this necessity for MED recognition of pathological graph structure dependence and representation relationships. However, OMCNIC significantly increased by 19.66%, 15.70%, 0.50% and 8.49% compared with the Inception-V3 model in accuracy, recall, precision and F1-score, respectively; and then, compared with VGG-16 model, our OMCNIC model increased by 6.16%, 13.60%, 5.95% and 10.30% in accuracy, recall, precision and F1-score, respectively. Because of the structural constraints between ME patches, the GIN model can be well constructed for unique and easy-to-learn middle ear pathological features, as expected, this shows the importance and high efficiency of the structural information representation features of middle ear pathology chart in the diagnosis of middle ear diseases.

Table 2 Comparison of our approach with the state-of-the-art approaches in CSOMCN classification
Full size table

Furthermore, for the class MEC that has very few samples or unbalanced samples, the GCNs could gain higher identification accuracy by take into account the form of a graph structure. In contrast, the CNN models cannot precisely model those classes. Nevertheless, it is notable that the structure-constrained deep feature fusion is capable of better identifying these challenging examples, due to the common use of the coordinate distance and the feature vector of nodes.

5 Discussion

The experimental results indicate that the enhanced GIN algorithm (i.e., OMCNIC) is obviously better than all the baseline models, including GIN, in terms of accuracy, and has obtained the best performance at present. These results show that OMCNIC has powerful graph structure modeling. This is mainly because OMCNIC not only inherits the powerful judgment power of GIN, but also uses structural feature information in graph structural modeling.

In the preprocessing phase, our preprocessing in medicine is faced with the exclusion and inclusion criteria, which need to be based on the clinical diagnostic criteria of CSOM and MEC, it includes reviewing the medical history, preoperative examination results, intraoperative and postoperative pathological findings, screening the patients’ data that accord with the standard of CT, and eliminating the patients’ data that have too much noise and do not accord with the requirement of CT; to do this, we asked experienced otolaryngology to sift through and remove the ear data that doesn’t meet our requirements. And then, when faced data imbalances during the technical pre-processing phase, reasonable data expansion and data enhancement are required, and because MEC patient data are scarce, we reused MEC data, adding inverted left ear MEC case data to the training of the right ear pathology classifier.

Graph isomorphism network (GIN) has the greatest ability to represent from different graph structures and has quantifiable generalization ability, which quickly attracted wide attention from the GNN community and the performance is better than other previous GNN framework. Nevertheless, the GIN has not sufficiently utilizing the features information of the structural graph, cannot to adequately take advantage its structural modeling capability. Based on the GIN, our work primarily utilizing the structural characteristics, i.e., the feature vector concentration and coordinate distance between the vertex and its neighbors, to heighten the graph structural modeling capacity and to promote identification of ME properties. Therefore, we proposed a better method to identify the ME properties, called OMCNIC, which is based on the improvement of GIN. We can obvious find that the OMCNIC performance is dramatically affected by the feature vector concatenation and coordinate weight regulation. Our OMCNIC was realized by cascading the feature vector of the vertex neighbors and the coordinate distance of the vertex, thus adjusting the neighborhood weight in the information cluster by adding a control gate unit.

In the future, we will expand and explore our further work from the following aspects: (1) continue to expand the sample size, cooperate with many medical institutions, carry out multi-center research, and further improve the generalizability and interpretability of the model; (2) single layer was used in this study, and we hope to improve the accuracy of small-scale lesions by analyzing the images from 3D multi-angle; (3) to expand the image of atypical cases, we hope to extend our algorithm to computer-aided diagnostics other middle ear and inner ear diseases. In addition, we look forward to developing a framework for the assistant diagnosis of middle ear diseases, it has great social benefits for the disease management of the ME and CSOM patient database, the construction of a multi-disciplinary team and the multi-center on-line combined diagnosis and treatment.

6 Conclusion

In this paper, our OMCNIC presents a promising method for the identification of large-scale middle ear diseases. The experimental results indicate that our structure-constrained deep feature fusion algorithm can quickly and effectively classify CSOM and MEC. The presented algorithm is also promising for other graph structural modeling problems in medical and biomedical domains. Nevertheless, like to other deep learning methods, our OMCNIC method still has a weakly interpretability. It is difficult to obviously recognize which sub- structures of the ME play significant roles in the identification challenge. In the future, we will continue our research in enhancing the model interpretability.