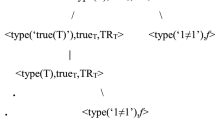Abstract
Curry’s paradox is well known. The original version employed a conditional connective, and is not forthcoming if the conditional does not satisfy contraction. A newer version uses a validity predicate, instead of a conditional, and is not forthcoming if validity does not satisfy structural contraction. But there is a variation of the paradox which uses “external validity” (that is, essentially, preservation of theoremhood). And since external validity contracts, one might expect the appropriate version of the Curry paradox to be inescapable. In this paper we show that this is not the case. We consider two ways of formalising the notion of external validity, and show that in both of these the paradox is not forthcoming without the appropriate forms of contraction.
Similar content being viewed by others
Notes
Or, assuming that → detaches and satisfies the Deduction Theorem, the contraction axiom schema (Law of Absorption): (A→(A → B)) → (A → B).
External validity is sometimes called ‘admissibility’. See, e.g., [4].
Or evenσ ≡ (T(σ¯) → A), where ‘≡’stands for syntactic identity.
Beall and Murzi require
$\vdash Val(\overline {A}, \overline {B}) \text {iff} A \vdash B$because they assume that validity claims are themselves valid if true.
We slightly change the notation. In particular, Beall and Murzi use an absurdity constant ⊥ instead of an arbitrary formula A.
According to Roy Cook [5], the assumption of self-referentiality makes the v-Curry reasoning dependent on some extra-logical theory such as Peano Arithmetic, so that there is no paradox of strictly logical validity. In the present case the reasoning depends on the (π − I) and (π − E) rules.
We use the sequent arrow ⇒ instead of the turnstile ⊩.
Von Kutschera [8] uses another version of (cut), namely
$ TR \quad {\Delta } \Rightarrow T; \, {\Delta }, T \Rightarrow U \vdash {\Delta } \Rightarrow U, $which on the one hand builds in a contraction to a single occurrence of Δ and on the other hand is less general than TR′. TR is interderivable with TR′ in the presence of VV, SK and ST. Since we will consider dropping VV or SK, we will use TR′ instead of TR.
In addition to PE′, von Kutschera also uses another premise introduction rule and says that it is equivalent with PE′, namely
$$PE \quad {\Delta} \Rightarrow {\Gamma}; \, {\Delta}, T \Rightarrow U \vdash {\Delta}, ({\Gamma} \Rightarrow T) \Rightarrow U $$where, due to the restriction to positive S-formulas, the sequence Γ must be non-empty. The rule PE also builds in a contraction to a single occurrence of Δ. Clearly, PE can be derived from PE′:

where * indicates (possibly repeated) uses of TR′, SK and ST. The converse, however, is problematic, because von Kutschera derives ( ⇒ T) ⇒ T from ( ⇒ T) ⇒( ⇒ T) by means of PE′ and thus allows Γ in PE′ to be empty. The obvious route to a derivation of PE′ from PE is blocked for empty Γ:

We will therefore use PE′ instead of PE.
Note that in the TR′-step of Theorem 1 we use SK, whereas the use of TR can be handled without any appeal to SK.
If TR′ were eliminable, the problem would disappear. But our use of PE′ instead of PE stands in the way of cut-elimination. A counter example to cut-elimination is the sequent (U ⇒ V),(T ⇒ U),T ⇒ V for \(\mathcal {L}\)-formulas T, U, V. It can be proved with the aid of TR′:

but has no cut-free proof.
References
Avron, A. (1988). The semantics and proof theory of linear logic. Theoretical Computer Science, 57, 161–184.
Beall, J. (2013). Curry’s Paradox In Zalta, E. N. (Ed.), The Stanford Encyclopedia of Philosophy. Spring Edition. http://plato.stanford.edu/archives/spr2013/entries/curry-paradox.
Beall, J., & Murzi, J. (2013). Two Flavors of Curry’s Paradox. The Journal of Philosophy, 110, 143–165.
Brady, R.T. (1994). Rules in Relevant Logic–I: Semantic Classification. Journal of Philosophical Logic, 23, 111–137.
Cook, R.T. (2014). There is No Paradox of Logical Validity. Logica Universalis. doi:10.1007/s11787014-0094-4.
Curry, H.B. (1942). The Inconsistency of Certain Formal Logics. Journal of Symbolic Logic, 7, 115–117.
Došen, K. (1988). Sequent Systems and Groupoid Models I. Studia Logica, 47, 353–389.
von Kutschera, F. (1968). Die Vollständigkeit des Operatorensystems {¬,∧,∨,⊃} für die intuitionistische Aussagenlogik im Rahmen der Gentzensemantik. Archiv für mathematische Logik und Grundlagenforschung, 11, 3–16.
Mares, E., & Paoli, F. (2014). Logical Consequence and the Paradoxes. Journal of Philosophical Logic, 43, 439–469.
Priest, G. (2013) Fusion and Confusion. Topoi. doi:10.1007/s11245-013-9175-x.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wansing, H., Priest, G. External Curries. J Philos Logic 44, 453–471 (2015). https://doi.org/10.1007/s10992-014-9336-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-014-9336-4