Epsilon-Trig Regularization Method for Bang-Bang Optimal Control Problems | Journal of Optimization Theory and Applications Skip to main content
Springer Nature Link
Log in

Epsilon-Trig Regularization Method for Bang-Bang Optimal Control Problems

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

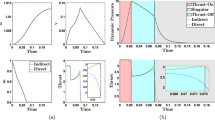
Bang-bang control problems have numerical issues due to discontinuities in the control structure and require smoothing when using optimal control theory that relies on derivatives. Traditional smooth regularization introduces a small error into the original problem using error controls and an error parameter to enable the construction of accurate smoothed solutions. When path constraints are introduced into the problem, the traditional smooth regularization fails to bound the error controls involved. It also introduces a dimensional inconsistency related to the error parameter. Moreover, the traditional approach solves for the error controls separately, which makes the problem formulation complicated for a large number of error controls. The proposed Epsilon-Trig regularization method was developed to address these issues by using trigonometric functions to impose implicit bounds on the controls. The system of state equations is modified such that the smoothed control is expressed in sine form, and only one of the state equations contains an error control in cosine form. Since the Epsilon-Trig method has an error parameter only in one state equation, there is no dimensional inconsistency. Moreover, the Epsilon-Trig method only requires the solution to one control, which greatly simplifies the problem formulation. Its simplicity and improved capability over the traditional smooth regularization method for a wide variety of problems including the Goddard rocket problem have been discussed in this study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Bertrand, R., Epenoy, R.: New smoothing techniques for solving bang-bang optimal control problems-numerical results and statistical interpretation. Optim. Control Appl. Methods 23(4), 171–197 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  2. Dadebo, S.A., McAuley, K.B.: On the computation of optimal singular controls. In Proceedings of the 4th IEEE Conference on Control Applications, pp. 150–155 (1995)

  3. Jacobson, D., Gershwin, S., Lele, M.: Computation of optimal singular controls. IEEE Trans. Autom. Control 15(1), 67–73 (1970)

    Article  MathSciNet  Google Scholar 

  4. Edgar, T.F., Lapidus, L.: The computation of optimal singular bang?bang control I: linear systems. AIChE J. 18(4), 774–779 (1972)

    Article  Google Scholar 

  5. Edgar, T.F., Lapidus, L.: The computation of optimal singular bang-bang control II: linear systems. AIChE J. 18(4), 780–785 (1972)

    Article  Google Scholar 

  6. Chen, Y., Huang, J.: A continuation method for singular optimal control synthesis. In: American Control Conference, IEEE, 1256–1260 (1993)

  7. Gergaud, J., J. Noailles: Application of simplicial algorithm to a spacecraft trajectory optimization problem. In: Seventh IFAC Workshop on Control Appl. of Nonlinear Prog. and Optim. (1988)

  8. Silva, C.J., Trélat, E.: Smooth regularization of bang-bang optimal control problems. IEEE Trans. Autom. Control 55(11), 2488–2499 (2010)

    Article  MathSciNet  Google Scholar 

  9. Longuski, J.M., Guzman, J.J., Prussing, J.E.: Optimal Control with Aerospace Applications. Springer, New York (2014)

    Book  MATH  Google Scholar 

  10. Mall, K., Grant, M.J.: Trigonomerization of Optimal Control Problems with Bounded Controls. AIAA Aviation Forum and Exposition, Washington D. C. (2016)

    Book  Google Scholar 

  11. Haberkorn, T., Martinon, P., Gergaud, J.: Low thrust minimum-fuel orbital transfer: a homotopic approach. J. Guid. Control Dyn. 27(6), 1046–1060 (2004)

    Article  Google Scholar 

  12. Taheri, E., Kolmanovsky, I., Atkins, E.: Enhanced smoothing technique for indirect optimization of minimum-fuel low-thrust trajectories. J. Guida. Control Dyn. 39(11), 2500–2511 (2016)

  13. Guo, T., Jiang, F., Li, J.: Homotopic approach and pseudospectral method applied jointly to low thrust trajectory optimization. Acta Astronautica 71, 38–50 (2012)

    Article  Google Scholar 

  14. Li, J., Xi, X.: Fuel-optimal low-thrust reconfiguration of formation-flying satellites via homotopic approach. J. Guid. Control Dyn 35(6), 1709–1717 (2012)

    Article  Google Scholar 

  15. Jiang, F., Baoyin, H., Li, J.: Practical techniques for low-thrust trajectory optimization with homotopic approach. J. Guid. Control Dyn. 35(1), 245–258 (2012)

    Article  Google Scholar 

  16. Kim, M.: Continuous Low-Thrust Trajectory Optimization: Techniques and Applications. Virginia Tech, Diss (2005)

    Google Scholar 

  17. Strang, G.: Linear Algebra and Its Applications. Springer, New York (2006)

    MATH  Google Scholar 

  18. Li, S., Zhao, R., Zhang, Q.: Optimization method for solving bang-bang and singular control problems. J. Control Theory Appl. 10(4), 559–564 (2012)

    Article  MathSciNet  Google Scholar 

  19. Patterson, M.A., Rao, A.V.: GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. (TOMS) 41(1), 1 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  20. Grant, M.J., Braun, R.D.: Rapid indirect trajectory optimization for conceptual design of hypersonic missions. J. Spacecr. Rockets 52(1), 177–182 (2015)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Purdue University, West Lafayette, IN, USA

    Kshitij Mall & Michael James Grant

Authors
  1. Kshitij Mall
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael James Grant
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kshitij Mall.

Additional information

Communicated by Ryan P. Russell.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mall, K., Grant, M.J. Epsilon-Trig Regularization Method for Bang-Bang Optimal Control Problems. J Optim Theory Appl 174, 500–517 (2017). https://doi.org/10.1007/s10957-017-1129-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-017-1129-9

Keywords

Mathematics Subject Classification

Search

Navigation