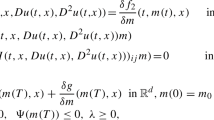Abstract
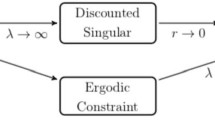
This work focuses on optimal controls of diffusions in an infinite horizon. It has several distinct features in contrast to the existing literature. The discount factor is allowed to be randomly varying and state dependent. The existence and uniqueness of the viscosity solution to the associated Hamilton–Jacobi–Bellman equation are established. The verification theorem is also obtained. Because closed-form solutions are virtually impossible to obtain in most cases, we develop numerical methods. Using the Markov chain approximation methods, numerical schemes are constructed; viscosity solution methods are used to prove the convergence of the algorithm. In addition, examples are given for demonstration purpose.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Polyak, B.T.: Introduction to Optimization, Translated from the Russian, Translations Series in Mathematics and Engineering. Optimization Software Inc, Publications Division, New York (1987)
Borkar, V.S., Arapostathis, A., Ghosh, M.K.: Ergodic Control of Diffusion Processes. Cambridge University Press, Cambridge (2012)
Fleming, W.H., Soner, H.M.: Controlled Markov Processes and Viscosity Solutions. Springer, New York (2006)
Kushner, H.J., Dupuis, P.: Numerical Methods for Stochastic Control Problems in Continuous Time. Springer, New York (2001)
Yong, J., Zhou, X.Y.: Stochastic Controls: Hamiltonian Systems and HJB Equations. Springer-Verlag, New York (1999)
Kushner, H.J.: Optimal discounted stochastic control for diffusion processes. SIAM J. Control Optim. 5, 520–531 (1967)
Fleming, W.H., Rishel, R.W.: Deterministic and Stochastic Optimal Control. Springer, New York (1975)
Crandall, M.G.: Viscosity solutions of Hamilton–Jacobi equations. Trans. Am. Math. Soc. 277, 1–41 (1983)
Lions, P.L.: Optimal control of diffusion processes and Hamilton–Jacobi–Bellman equations part 2: viscosity solutions and uniqueness. Commun. PDE 8, 1229–1276 (1983)
Souganidis, P.E., Barles, G.: Convergence of approximation schemes for fully nonlinear second order equations. Asymptot. Anal. 4, 271–283 (1991)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer-Verlag, New York (2001)
Ishii, H.: On uniqueness and existence of viscosity solutions of fully nonlinear second-order elliptic PDEs. Commun. Pure Appl. Math. XLII, 15–45 (1989)
Hernádez-Lerma, O., Lasserre, J.B.: Further Topics on Discrete-Time Markov Control Processes. Springer, New York (1999)
Pemy, M., Zhang, Q., Yin, G.: Liquidation of a large block of stock. J. Bank Finance 31, 1295–1305 (2007)
Jasso-Fuentes, H., Yin, G.: Advanced Criteria for Controlled Markov-Modulated Diffusions in an Infinite Horizon: Overtaking, Bias, and Blackwell Optimality. Science Press, Beijing (2013)
Acknowledgments
Research of X. Lu was supported in part by the International Program for Ph.D. candidates of Sun Yat-Sen University. Research of G. Yin was supported in part by the Air Force Office of Scientific Research under FA9550-15-1-0131. Research of X. Guo was supported in part by the National Natural Science Foundation of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lu, X., Yin, G. & Guo, X. Infinite Horizon Controlled Diffusions with Randomly Varying and State-Dependent Discount Cost Rates. J Optim Theory Appl 172, 535–553 (2017). https://doi.org/10.1007/s10957-016-0898-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-016-0898-x
Keywords
- Controlled diffusion
- Random and state-dependent discount cost rate
- Hamilton–Jacobi–Bellman equation
- Verification theorem
- Numerical approximation