High-Order Finite-Volume TENO Schemes with Dual ENO-Like Stencil Selection for Unstructured Meshes | Journal of Scientific Computing Skip to main content
Springer Nature Link
Log in

High-Order Finite-Volume TENO Schemes with Dual ENO-Like Stencil Selection for Unstructured Meshes

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

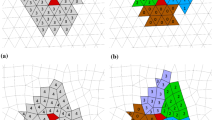
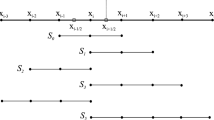
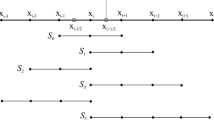
The TENO-family schemes (Fu et al. in J Comput Phys 305: 333–359, 2016) have been demonstrated to perform well for compressible gas dynamics and turbulent flow predictions on structured meshes. However, the extension of the TENO schemes to unstructured meshes is non-trivial and challenging, particularly when the multiple design objectives are pursued simultaneously, i.e., restoring the high-order accuracy in smooth regions, retaining the low numerical dissipation for small-scale features, maintaining the sharp shock-capturing property, and featuring the good numerical robustness for high-Mach flows. In this work, a family of very-high-order (up to seventh-order accuracy) robust finite-volume TENO schemes with dual ENO-like stencil selection for unstructured meshes is proposed. The stencils include one large stencil and several small stencils. The novelty originates from a so-called dual ENO-like stencil selection strategy. Following a strong scale separation, the ENO-like stencil selection procedure with a small \(C_T\) is first enforced among all the candidates such that the high-order candidate scheme on the large stencil is adopted for the final reconstruction when the local flow is smooth. If the large stencil is judged to be crossed by discontinuities, a second ENO-like stencil selection with a relatively large \(C_T\) is applied to all the left small stencils and the ENO property is obtained by selecting the smooth small stencils which are not crossed by discontinuities. The smaller \(C_T\) in the first stage ensures that the high-order reconstruction is restored for smooth flow scales with higher wavenumbers. On the other hand, the larger \(C_T\) in the second stage can enforce a strong nonlinear adaptation for capturing discontinuities with better robustness. Such a dual ENO-like stencil selection strategy introduces an explicit scale separation and deploys the optimal strategy for different types of flows correspondingly. Without parameter tuning, a set of benchmark simulations has been conducted to validate the performance of the proposed TENO schemes. Numerical results demonstrate the good numerical robustness and the low-dissipation property for highly compressible flows with shockwaves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  1. Shu, C.-W.: High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 51(1), 82–126 (2009)

    MathSciNet  MATH  Google Scholar 

  2. Pirozzoli, S.: Numerical methods for high-speed flows. Annu. Rev. Fluid Mech. 43, 163–194 (2011)

    MathSciNet  MATH  Google Scholar 

  3. Fu, L., Karp, M., Bose, S.T., Moin, P., Urzay, J.: Shock-induced heating and transition to turbulence in a hypersonic boundary layer. J. Fluid Mech. 909, A8 (2021)

    MathSciNet  MATH  Google Scholar 

  4. Fu, L., Bose, S., Moin, P.: Prediction of aerothermal characteristics of a generic hypersonic inlet flow. Theor. Comput. Fluid Dyn. 36(2), 345–368 (2022)

    MathSciNet  Google Scholar 

  5. Griffin, K.P., Fu, L., Moin, P.: Velocity transformation for compressible wall-bounded turbulent flows with and without heat transfer. Proc. Natl. Acad. Sci. 118(34), e2111144118 (2021)

    MathSciNet  Google Scholar 

  6. Johnsen, E., Larsson, J., Bhagatwala, A.V., Cabot, W.H., Moin, P., Olson, B.J., Rawat, P.S., Shankar, S.K., Sjögreen, B., Yee, H., Zhong, X., Lele, S.K.: Assessment of high-resolution methods for numerical simulations of compressible turbulence with shock waves. J. Comput. Phys. 229(4), 1213–1237 (2010)

    MathSciNet  MATH  Google Scholar 

  7. Fu, L., Hu, X.Y., Adams, N.A.: A targeted ENO scheme as implicit model for turbulent and genuine subgrid scales. Commun. Comput. Phys. 26(2), 311–345 (2019)

    MathSciNet  MATH  Google Scholar 

  8. Fu, L., Hu, X.Y., Adams, N.A.: Improved five- and six-point targeted essentially nonoscillatory schemes with adaptive dissipation. AIAA J. 57(3), 1143–1158 (2019)

    Google Scholar 

  9. von Neumann, J., Richtmyer, R.D.: A method for the numerical calculation of hydrodynamic shocks. J. Appl. Phys. 21(3), 232–237 (1950)

    MathSciNet  MATH  Google Scholar 

  10. Jameson, A.: Analysis and design of numerical schemes for gas dynamics, 1: artificial diffusion, upwind biasing, limiters and their effect on accuracy and multigrid convergence. Int. J. Comput. Fluid Dyn. 4, 171–218 (1994)

    Google Scholar 

  11. Harten, A.: High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49, 357–393 (1983)

    MathSciNet  MATH  Google Scholar 

  12. Kim, K.H., Kim, C.: Accurate, efficient and monotonic numerical methods for multi-dimensional compressible flows part II: multi-dimensional limiting process. J. Comput. Phys. 208, 570–615 (2005)

    MATH  Google Scholar 

  13. Harten, A., Engquist, B., Osher, S., Chakravarthy, S.R.: Uniformly high order accurate essentially non-oscillatory schemes, III. J. Comput. Phys. 71, 231–303 (1987)

    MathSciNet  MATH  Google Scholar 

  14. Liu, X.D., Osher, S., Chan, T.: Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115, 200–212 (1994)

    MathSciNet  MATH  Google Scholar 

  15. Jiang, G.S., Shu, C.-W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126(1), 202–228 (1996)

    MathSciNet  MATH  Google Scholar 

  16. Henrick, A.K., Aslam, T., Powers, J.M.: Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points. J. Comput. Phys. 207, 542–567 (2005)

    MATH  Google Scholar 

  17. Borges, R., Carmona, M., Costa, B., Don, W.S.: An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 227, 3191–3211 (2008)

    MathSciNet  MATH  Google Scholar 

  18. Acker, F., Borges, R.D.R., Costa, B.: An improved WENO-Z scheme. J. Comput. Phys. 313, 726–753 (2016)

    MathSciNet  MATH  Google Scholar 

  19. Hill, D., Pullin, D.: Hybrid tuned center-difference-WENO method for large eddy simulations in the presence of strong shocks. J. Comput. Phys. 194, 435–450 (2004)

    MATH  Google Scholar 

  20. Weirs, V., Candler, G.: Optimization of weighted ENO schemes for DNS of compressible turbulence. In: AIAA Paper, pp. 97–1940 (1997)

  21. Martín, M.P., Taylor, E.M., Wu, M., Weirs, V.G.: A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence. J. Comput. Phys. 220(1), 270–289 (2006)

    MATH  Google Scholar 

  22. Ghosh, D., Baeder, J.D.: Compact reconstruction schemes with weighted ENO limiting for hyperbolic conservation laws. SIAM J. Sci. Comput. 34(3), A1678–A1706 (2012)

    MathSciNet  MATH  Google Scholar 

  23. Hu, X.Y., Wang, Q., Adams, N.A.: An adaptive central-upwind weighted essentially non-oscillatory scheme. J. Comput. Phys. 229, 8952–8965 (2010)

    MathSciNet  MATH  Google Scholar 

  24. Balsara, D.S., Shu, C.-W.: Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J. Comput. Phys. 160(2), 405–452 (2000)

    MathSciNet  MATH  Google Scholar 

  25. Gerolymos, G., Sénéchal, D., Vallet, I.: Very-high-order WENO schemes. J. Comput. Phys. 228, 8481–8524 (2009)

    MathSciNet  MATH  Google Scholar 

  26. Adams, N., Shariff, K.: A high-resolution hybrid compact-ENO scheme for shock–turbulence interaction problems. J. Comput. Phys. 127(1), 27–51 (1996)

    MathSciNet  MATH  Google Scholar 

  27. Pirozzoli, S.: Conservative hybrid compact-WENO schemes for shock–turbulence interaction. J. Comput. Phys. 178(1), 81–117 (2002)

    MathSciNet  MATH  Google Scholar 

  28. Ren, Y.-X., Liu, M., Zhang, H.: A characteristic-wise compact WENO scheme for solving hyperbolic conservation laws. J. Comput. Phys. 192, 365–386 (2003)

    MathSciNet  MATH  Google Scholar 

  29. Shu, C.-W.: Essentially non-oscillatory and weighted essentially non-oscillatory schemes. Acta Numer. 29, 701–762 (2020)

    MathSciNet  MATH  Google Scholar 

  30. Fu, L., Hu, X.Y., Adams, N.A.: A family of high-order targeted ENO schemes for compressible-fluid simulations. J. Comput. Phys. 305, 333–359 (2016)

    MathSciNet  MATH  Google Scholar 

  31. Fu, L., Hu, X.Y., Adams, N.A.: Targeted ENO schemes with tailored resolution property for hyperbolic conservation laws. J. Comput. Phys. 349, 97–121 (2017)

    MathSciNet  MATH  Google Scholar 

  32. Fu, L., Hu, X.Y., Adams, N.A.: A new class of adaptive high-order targeted ENO schemes for hyperbolic conservation laws. J. Comput. Phys. 374, 724–751 (2018)

    MathSciNet  MATH  Google Scholar 

  33. Fu, L.: A low-dissipation finite-volume method based on a new TENO shock-capturing scheme. Comput. Phys. Commun. 235, 25–39 (2019)

    MathSciNet  MATH  Google Scholar 

  34. Haimovich, O., Frankel, S.H.: Numerical simulations of compressible multicomponent and multiphase flow using a high-order targeted ENO (TENO) finite-volume method. Comput. Fluids 146, 105–116 (2017)

    MathSciNet  MATH  Google Scholar 

  35. Dong, H., Fu, L., Zhang, F., Liu, Y., Liu, J.: Detonation simulations with a fifth-order TENO scheme. Commun. Comput. Phys. 25, 1357–1393 (2019)

    MathSciNet  MATH  Google Scholar 

  36. Fu, L., Tang, Q.: High-order low-dissipation targeted ENO schemes for ideal magnetohydrodynamics. J. Sci. Comput. 80(1), 692–716 (2019)

    MathSciNet  MATH  Google Scholar 

  37. Fu, L.: An efficient low-dissipation high-order TENO scheme for MHD flows. J. Sci. Comput. 90(1), 1–24 (2022)

    MathSciNet  MATH  Google Scholar 

  38. Sun, Z., Inaba, S., Xiao, F.: Boundary variation diminishing (BVD) reconstruction: a new approach to improve Godunov schemes. J. Comput. Phys. 322, 309–325 (2016)

    MathSciNet  MATH  Google Scholar 

  39. Zhao, G.-Y., Sun, M.-B., Pirozzoli, S.: On shock sensors for hybrid compact/WENO schemes. Comput. Fluids 199, 104439 (2020)

    MathSciNet  MATH  Google Scholar 

  40. Zhang, H., Zhang, F., Liu, J., McDonough, J., Xu, C.: A simple extended compact nonlinear scheme with adaptive dissipation control. Commun. Nonlinear Sci. Numer. Simul. 84, 105191 (2020)

    MathSciNet  MATH  Google Scholar 

  41. Zhang, H., Zhang, F., Xu, C.: Towards optimal high-order compact schemes for simulating compressible flows. Appl. Math. Comput. 355, 221–237 (2019)

    MathSciNet  MATH  Google Scholar 

  42. Fardipour, K., Mansour, K.: Development of targeted compact nonlinear scheme with increasingly high order of accuracy. Int. J. Prog. Comput. Fluid Dyn. 20(1), 1–19 (2020)

    MathSciNet  Google Scholar 

  43. Ye, C.-C., Zhang, P.-J.-Y., Wan, Z.-H., Sun, D.-J.: An alternative formulation of targeted ENO scheme for hyperbolic conservation laws. Comput. Fluids 238, 105368 (2022)

    MathSciNet  MATH  Google Scholar 

  44. Wang, L., Tian, F.-B., Lai, J.C.: An immersed boundary method for fluid-structure-acoustics interactions involving large deformations and complex geometries. J. Fluids Struct. 95, 102993 (2020)

    Google Scholar 

  45. Di Renzo, M., Fu, L., Urzay, J.: HTR solver: an open-source exascale-oriented task-based multi-GPU high-order code for hypersonic aerothermodynamics. Comput. Phys. Commun. 255, 107262 (2020)

    MathSciNet  Google Scholar 

  46. Motheau, E., Wakefield, J.: Investigation of finite-volume methods to capture shocks and turbulence spectra in compressible flows. Commun. Appl. Math. Comput. Sci. 15, 1–36 (2020)

    MathSciNet  MATH  Google Scholar 

  47. Lusher, D.J., Sandham, N.D.: Shock-wave/boundary-layer interactions in transitional rectangular duct flows. Flow Turbul. Combust. 105(2), 649–670 (2020)

    Google Scholar 

  48. Lusher, D., Jammy, S., Sandham, N.: Transitional shockwave/boundary-layer interactions in the automatic source-code generation framework OpenSBLI. In: Tenth international conference on computational fluid dynamics (ICCFD10) (2018)

  49. Lefieux, J., Garnier, E., Sandham, N.: DNS study of roughness-induced transition at mach 6. In: AIAA Aviation 2019 Forum, p. 3082 (2019)

  50. Lusher, D.J., Sandham, N.: Assessment of low-dissipative shock-capturing schemes for transitional and turbulent shock interactions. In: AIAA Aviation 2019 Forum (2019)

  51. Fu, L.: A hybrid method with TENO based discontinuity indicator for hyperbolic conservation laws. Commun. Comput. Phys. 26, 973–1007 (2019)

    MathSciNet  MATH  Google Scholar 

  52. Fu, L.: A very-high-order TENO scheme for all-speed gas dynamics and turbulence. Comput. Phys. Commun. 244, 117–131 (2019)

    MathSciNet  MATH  Google Scholar 

  53. Fu, L.: Very-high-order TENO schemes with adaptive accuracy order and adaptive dissipation control. Comput. Methods Appl. Mech. Eng. 387, 114193 (2021)

    MathSciNet  MATH  Google Scholar 

  54. Antoniadis, A.F., Drikakis, D., Farmakis, P.S., Fu, L., Kokkinakis, I., Nogueira, X., Silva, P.A., Skote, M., Titarev, V., Tsoutsanis, P.: UCNS3D: an open-source high-order finite-volume unstructured CFD solver. Comput. Phys. Commun. 279, 108453 (2022)

    MathSciNet  MATH  Google Scholar 

  55. Ji, Z., Liang, T., Fu, L.: A class of new high-order finite-volume TENO schemes for hyperbolic conservation laws with unstructured meshes. J. Sci. Comput. 92(2), 61 (2022)

    MathSciNet  MATH  Google Scholar 

  56. Lusher, D.J., Jammy, S.P., Sandham, N.D.: OpenSBLI: automated code-generation for heterogeneous computing architectures applied to compressible fluid dynamics on structured grids. Comput. Phys. Commun. 267, 108063 (2021)

    MathSciNet  Google Scholar 

  57. Hoppe, N., Winter, J.M., Adami, S., Adams, N.A.: ALPACA-a level-set based sharp-interface multiresolution solver for conservation laws. Comput. Phys. Commun. 272, 108246 (2022)

    MathSciNet  Google Scholar 

  58. Fu, L.: Review of the high-order TENO schemes for compressible gas dynamics and turbulence. Arch. Comput. Methods Eng. 30, 2493–2526 (2023)

    MathSciNet  Google Scholar 

  59. Hu, C., Shu, C.-W.: Weighted essentially non-oscillatory schemes on triangular meshes. J. Comput. Phys. 150(1), 97–127 (1999)

    MathSciNet  MATH  Google Scholar 

  60. Zhang, Y.-T., Shu, C.-W.: Third order WENO scheme on three dimensional tetrahedral meshes. Commun. Comput. Phys. 5(2–4), 836–848 (2009)

    MathSciNet  MATH  Google Scholar 

  61. Shi, J., Hu, C., Shu, C.-W.: A technique of treating negative weights in WENO scheme. J. Comput. Phys. 175, 108–127 (2002)

    MATH  Google Scholar 

  62. Cheng, J., Shu, C.-W.: A third order conservative Lagrangian type scheme on curvilinear meshes for the compressible Euler equations. Commun. Comput. Phys. 4, 1008–1024 (2008)

    MATH  Google Scholar 

  63. Dumbser, M., Käser, M.: Arbitrary high order non-oscillatory finite volume schemes on unstructured meshes for linear hyperbolic systems. J. Comput. Phys. 221(2), 693–723 (2007)

    MathSciNet  MATH  Google Scholar 

  64. Dumbser, M., Käser, M., Titarev, V.A., Toro, E.F.: Quadrature-free non-oscillatory finite volume schemes on unstructured meshes for nonlinear hyperbolic systems. J. Comput. Phys. 226(1), 204–243 (2007)

    MathSciNet  MATH  Google Scholar 

  65. Liu, Y., Zhang, Y.-T.: A robust reconstruction for unstructured WENO schemes. J. Sci. Comput. 54(2–3), 603–621 (2013)

    MathSciNet  MATH  Google Scholar 

  66. Zhu, J., Shu, C.-W.: A new type of multi-resolution WENO schemes with increasingly higher order of accuracy on triangular meshes. J. Comput. Phys. 392, 19–33 (2019)

    MathSciNet  MATH  Google Scholar 

  67. Zhu, J., Shu, C.-W.: A new type of third-order finite volume multi-resolution WENO schemes on tetrahedral meshes. J. Comput. Phys. 406, 109212 (2020)

    MathSciNet  MATH  Google Scholar 

  68. Balsara, D.S., Garain, S., Florinski, V., Boscheri, W.: An efficient class of WENO schemes with adaptive order for unstructured meshes. J. Comput. Phys. 404, 109062 (2020)

    MathSciNet  MATH  Google Scholar 

  69. Levy, D., Puppo, G., Russo, G.: Central WENO schemes for hyperbolic systems of conservation laws. ESAIM: Math. Model. Numer. Anal. 33(3), 547–571 (1999)

    MathSciNet  MATH  Google Scholar 

  70. Levy, D., Puppo, G., Russo, G.: Compact central WENO schemes for multidimensional conservation laws. SIAM J. Sci. Comput. 22(2), 656–672 (2000)

    MathSciNet  MATH  Google Scholar 

  71. Capdeville, G.: A central WENO scheme for solving hyperbolic conservation laws on non-uniform meshes. J. Comput. Phys. 227(5), 2977–3014 (2008)

    MathSciNet  MATH  Google Scholar 

  72. Tsoutsanis, P., Adebayo, E.M., Merino, A.C., Arjona, A.P., Skote, M.: CWENO finite-volume interface capturing schemes for multicomponent flows using unstructured meshes. J. Sci. Comput. 89, 1–27 (2021)

    MathSciNet  MATH  Google Scholar 

  73. Tsoutsanis, P., Kumar, M.S.S.P., Farmakis, P.S.: A relaxed a posteriori MOOD algorithm for multicomponent compressible flows using high-order finite-volume methods on unstructured meshes. Appl. Math. Comput. 437, 127544 (2023)

    MathSciNet  MATH  Google Scholar 

  74. Boscheri, W., Semplice, M., Dumbser, M., et al.: Central WENO subcell finite volume limiters for ADER discontinuous Galerkin schemes on fixed and moving unstructured meshes. Commun. Comput. Phys. 25(2), 311–346 (2019)

    MathSciNet  MATH  Google Scholar 

  75. Maltsev, V., Yuan, D., Jenkins, K.W., Skote, M., Tsoutsanis, P.: Hybrid discontinuous Galerkin-finite volume techniques for compressible flows on unstructured meshes. J. Comput. Phys. 473, 111755 (2023)

    MathSciNet  MATH  Google Scholar 

  76. Tsoutsanis, P., Titarev, V.A., Drikakis, D.: WENO schemes on arbitrary mixed-element unstructured meshes in three space dimensions. J. Comput. Phys. 230(4), 1585–1601 (2011)

    MathSciNet  MATH  Google Scholar 

  77. Titarev, V., Tsoutsanis, P., Drikakis, D.: WENO schemes for mixed-element unstructured meshes. Commun. Comput. Phys. 8(3), 585 (2010)

    MathSciNet  MATH  Google Scholar 

  78. Tsoutsanis, P.: Stencil selection algorithms for WENO schemes on unstructured meshes. J. Comput. Phys.: X 4, 100037 (2019)

    MathSciNet  Google Scholar 

  79. Tsoutsanis, P., Dumbser, M.: Arbitrary high order central non-oscillatory schemes on mixed-element unstructured meshes. Comput. Fluids 225, 104961 (2021)

    MathSciNet  MATH  Google Scholar 

  80. Tsoutsanis, P., Antoniadis, A.F., Drikakis, D.: WENO schemes on arbitrary unstructured meshes for laminar, transitional and turbulent flows. J. Comput. Phys. 256, 254–276 (2014)

    MathSciNet  MATH  Google Scholar 

  81. Tsoutsanis, P., Antoniadis, A.F., Jenkins, K.W.: Improvement of the computational performance of a parallel unstructured WENO finite volume CFD code for implicit large Eddy simulation. Comput. Fluids 173, 157–170 (2018)

    MathSciNet  MATH  Google Scholar 

  82. Toro, E.F.: Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer, Berlin (2013)

    Google Scholar 

  83. Harten, A., Lax, P.D., Leer, B.V.: On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev. 25(1), 35–61 (1983)

    MathSciNet  MATH  Google Scholar 

  84. Toro, E.F., Spruce, M., Speares, W.: Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 4(1), 25–34 (1994)

    MATH  Google Scholar 

  85. Einfeldt, B., Munz, C.-D., Roe, P.L., Sjögreen, B.: On Godunov-type methods near low densities. J. Comput. Phys. 92(2), 273–295 (1991)

    MathSciNet  MATH  Google Scholar 

  86. Batten, P., Clarke, N., Lambert, C., Causon, D.M.: On the choice of wavespeeds for the HLLC Riemann solver. SIAM J. Sci. Comput. 18(6), 1553–1570 (1997)

    MathSciNet  MATH  Google Scholar 

  87. Gressier, J., Moschetta, J.-M.: Robustness versus accuracy in shock-wave computations. Int. J. Numer. Methods Fluids 33(3), 313–332 (2000)

    MATH  Google Scholar 

  88. Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43(1), 89–112 (2001)

    MathSciNet  MATH  Google Scholar 

  89. LeVeque, R.J.: High-resolution conservative algorithms for advection in incompressible flow. SIAM J. Numer. Anal. 33(2), 627–665 (1996)

    MathSciNet  MATH  Google Scholar 

  90. Shu, C.W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes, II. J. Comput. Phys. 83, 32–78 (1989)

    MathSciNet  MATH  Google Scholar 

  91. Woodward, P.: The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comput. Phys. 54, 115–173 (1984)

    MathSciNet  MATH  Google Scholar 

  92. Liang, T., Xiao, F., Shyy, W., Fu, L.: A fifth-order low-dissipation discontinuity-resolving TENO scheme for compressible flow simulation. J. Comput. Phys. 467, 111465 (2022)

    MathSciNet  MATH  Google Scholar 

  93. Van Dyke, M.: An Album of Fluid Motion, vol. 176. Parabolic Press, Stanford (1982)

    Google Scholar 

  94. Zeng, X., Scovazzi, G.: A frame-invariant vector limiter for flux corrected nodal remap in arbitrary Lagrangian–Eulerian flow computations. J. Comput. Phys. 270, 753–783 (2014)

    MathSciNet  MATH  Google Scholar 

Download references

Funding

Z.J. is supported by the Fundamental Research Funds for the Central Universities (No. D5000210971), Guangdong Basic and Applied Basic Research Foundation (No. 2022A1515110314), and the General Program of Taicang Basic Research Project (No. TC2022JC07). L.F. acknowledges the fund from the Research Grants Council (RGC) of the Government of Hong Kong Special Administrative Region (HKSAR) with RGC/ECS Project (No. 26200222), the fund from Guangdong Basic and Applied Basic Research Foundation (No. 2022A1515011779), and the fund from the Project of Hetao Shenzhen-Hong Kong Science and Technology Innovation Cooperation Zone (No. HZQB-KCZYB-2020083).

Author information

Authors and Affiliations

  1. School of Software, Northwestern Polytechnical University, Xi’an, 710072, China

    Zhe Ji

  2. Yangtze River Delta Research Institute of NPU, Taicang, Jiangsu, China

    Zhe Ji

  3. Department of Mechanical and Aerospace Engineering, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong

    Tian Liang & Lin Fu

  4. Department of Mathematics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong

    Lin Fu

  5. HKUST Shenzhen-Hong Kong Collaborative Innovation Research Institute, Futian, Shenzhen, China

    Lin Fu

Authors
  1. Zhe Ji
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tian Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lin Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lin Fu.

Ethics declarations

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ji, Z., Liang, T. & Fu, L. High-Order Finite-Volume TENO Schemes with Dual ENO-Like Stencil Selection for Unstructured Meshes. J Sci Comput 95, 76 (2023). https://doi.org/10.1007/s10915-023-02199-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02199-1

Keywords

Search

Navigation