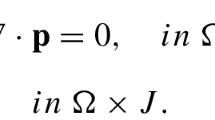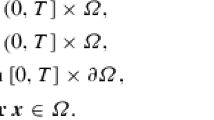A Second-order Time-Accurate Unconditionally Stable Method for a Gradient Flow for the Modica–Mortola Functional | Journal of Scientific Computing Skip to main content
Springer Nature Link
Log in

A Second-order Time-Accurate Unconditionally Stable Method for a Gradient Flow for the Modica–Mortola Functional

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

In this study, we present a second-order time-accurate unconditionally stable numerical method for a gradient flow for the Modica–Mortola functional with an equispaced multiple well potential. The proposed second-order time-accurate unconditionally stable numerical method is based on the operator splitting method. The nonlinear and linear terms in the gradient flow are solved analytically and using the Fourier spectral method, respectively. The numerical solutions in each step are bounded for any time step size and the overall scheme is temporally second-order accurate. We prove theoretically the unconditional stability and boundedness of the numerical solutions. In addition, several numerical tests are conducted to demonstrate the performance of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data Availability

Enquiries about data availability should be directed to the authors.

References

  1. Du, Q., Feng, X.: The phase field method for geometric moving interfaces and their numerical approximations. Handb. Numer. Anal. 21, 425–508 (2020)

    MathSciNet  MATH  Google Scholar 

  2. Garcia-Cardona, C., Merkurjev, E., Bertozzi, A.L., Flenner, A., Percus, A.G.: Multiclass data segmentation using diffuse interface methods on graphs. IEEE Trans. Pattern Anal. Mach. Intell. 36(8), 1600–1613 (2014)

    Article  MATH  Google Scholar 

  3. Giga, Y., Okamoto, J., Uesaka, M.: A finer singular limit of a single-well Modica-Mortola functional and its applications to the Kobayashi-Warren-Carter energy. Adv. Calc. Var. 16(1), 163–82 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  4. Gong, Y., Zhao, J., Wang, Q.: An energy stable algorithm for a quasi-incompressible hydrodynamic phase-field model of viscous fluid mixtures with variable densities and viscosities. Comput. Phys. Commun. 219, 20–34 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  5. Gong, Y., Zhao, J., Wang, Q.: Second order fully discrete energy stable methods on staggered grids for hydrodynamic phase field models of binary viscous fluids. SIAM J. Sci. Comput. 40(2), B528–B553 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ham, S., Hwang, Y., Kwak, S., Kim, J.: Unconditionally stable second-order accurate scheme for a parabolic sine-Gordon equation. AIP Adv. 12(2), 025203 (2022)

    Article  Google Scholar 

  7. Hötzer, J., Reiter, A., Hierl, H., Steinmetz, P., Selzer, M., Nestler, B.: The parallel multi-physics phase-field framework Pace3D. J. Comput. Sci. 26, 1–12 (2018)

    Article  MathSciNet  Google Scholar 

  8. Jin, B., Xu, Y.: Adaptive reconstruction for electrical impedance tomography with a piecewise constant conductivity. Inverse Probl. 36(1), 014003 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Jeong, D., Kim, J.: An explicit hybrid finite difference scheme for the Allen-Cahn equation. J. Comput. Appl. Math. 340, 247–255 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  10. Jung, Y.M., Kang, S.H., Shen, J.: Multiphase image segmentation via Modica-Mortola phase transition. SIAM J. Appl. Math. 67(5), 1213–1232 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  11. Kim, H., Yun, A., Yoon, S., Lee, C., Park, J., Kim, J.: Pattern formation in reaction-diffusion systems on evolving surfaces. Comput. Math. Appl. 80, 2019–2028 (2020)

    MathSciNet  MATH  Google Scholar 

  12. Lee, H.G.: A semi-analytical Fourier spectral method for the Swift-Hohenberg equation. Comput. Math. Appl. 74(8), 1885–1896 (2017)

    MathSciNet  MATH  Google Scholar 

  13. Lee, H.G., Shin, J., Lee, J.Y.: Energy quadratization Runge-Kutta scheme for the conservative Allen-Cah equation with a nonlocal Lagrange multiplier. Appl. Math. Lett. 132, 108161 (2022)

    Article  MATH  Google Scholar 

  14. Li, C., Huang, Y., Yi, N.: An unconditionally energy stable second order finite element method for solving the Allen-Cahn equation. J. Comput. Appl. Math. 353, 38–48 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  15. Li, D., Quan, C., Xu, J.: Stability and convergence of strang splitting. Part I: Scalar Allen-Cahn equation. J. Comput. Phys. 458, 111087 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, Y., Yoon, S., Wang, J., Park, J., Kim, S., Lee, C., Kim, J.: Fast and efficient numerical finite difference method for multiphase image segmentation. Math. Probl. Eng. 2021, 1–23 (2021)

    Article  Google Scholar 

  17. Li, Y., Kim, J.: Multiphase image segmentation using a phase-field model. Comput. Math. Appl. 62(2), 737–745 (2011)

    MathSciNet  MATH  Google Scholar 

  18. Ma, R., Sun, W.: FFT-based solver for higher-order and multi-phase-field fracture models applied to strongly anisotropic brittle materials. Comput. Meth. Appl. Mech. Eng. 362, 112781 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  19. Meny, J., Rumpf, M., Sassen, J.: A phase-field approach to variational hierarchical surface segmentation. Comput. Aided Geom. Des. 89, 102025 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  20. Wang, Q., Zhang, G., Li, Y., Hong, Z., Wang, D., Shi, S.: Application of phase-field method in rechargeable batteries. Npj Comput. Mater. 6(1), 1–8 (2020)

    Article  Google Scholar 

  21. Rong, Z., Wang, L.L., Tai, X.C.: Adaptive wavelet collocation methods for image segmentation using TV-Allen-Cahn type models. Adv. Comput. Math. 38(1), 101–131 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhao, X., Wang, Q.: A second order fully-discrete linear energy stable scheme for a binary compressible viscous fluid model. J. Comput. Phys. 395, 382–409 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  23. Zhang, C., Ouyang, J., Wang, X., Chai, Y., Ma, M.: Analysis of the energy stability for stabilized semi-implicit schemes of the functionalized Cahn-Hilliard Mass-conserving gradient flow equation. J. Sci. Comput. 87(1), 1–25 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  24. Zheng, N., Li, X.: Error analysis of the SAV Fourier-spectral method for the Cahn-Hilliard-Hele-Shaw system. Adv. Comput. Math. 47(5), 1–27 (2021)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first author (S. Ham) was supported by the National Research Foundation (NRF), Korea, under project BK21 FOUR. The corresponding author (J.S. Kim) expresses thanks for the support from the BK21 FOUR program. The authors would like to thank the reviewers for their useful comments and suggestions that helped to improve the paper.

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Department of Mathematics, Korea University, Seoul, 02841, Republic of Korea

    Seokjun Ham, Soobin Kwak, Chaeyoung Lee, Gyeonggyu Lee & Junseok Kim

Authors
  1. Seokjun Ham
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Soobin Kwak
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chaeyoung Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Gyeonggyu Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Junseok Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Junseok Kim.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ham, S., Kwak, S., Lee, C. et al. A Second-order Time-Accurate Unconditionally Stable Method for a Gradient Flow for the Modica–Mortola Functional. J Sci Comput 95, 63 (2023). https://doi.org/10.1007/s10915-023-02198-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02198-2

Keywords

Mathematics Subject Classification

Search

Navigation