Fractional Collocation Method for Third-Kind Volterra Integral Equations with Nonsmooth Solutions | Journal of Scientific Computing Skip to main content
Springer Nature Link
Log in

Fractional Collocation Method for Third-Kind Volterra Integral Equations with Nonsmooth Solutions

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

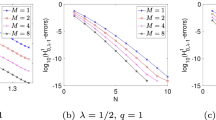
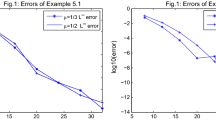
In this paper, we develop a collocation method for solving third-kind Volterra integral equations. In order to achieve high order convergence for problems with nonsmooth solutions, we construct a collocation scheme on a modified graded mesh using a basis of fractional polynomials, depending on a certain parameter \(\lambda \). For the proposed method, we derive an error estimate in the \(L^\infty \)-norm, which shows that the optimal order of global convergence can be obtained by choosing the appropriate parameter \(\lambda \) and modified mesh, even when the exact solution has low regularity. Numerical experiments confirm the theoretical results and illustrate the performance of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

All data generated or analysed during this study are included in this published article.

References

  1. Allaei, S.S., Yang, Z., Brunner, H.: Existence, uniqueness and regularity of solutions to a class of third-kind Volterra integral equations. J. Integral Equ. Appl. 27(3), 325–342 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  2. Allaei, S.S., Yang, Z., Brunner, H.: Collocation methods for third-kind VIEs. IMA J. Numer. Anal. 37(3), 1104–1124 (2017)

    MathSciNet  MATH  Google Scholar 

  3. Brunner, H.: Nonpolynomial spline collocation for Volterra equations with weakly singular kernels. SIAM J. Numer. Anal. 20(6), 1106–1119 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Brunner, H.: Collocation Methods for Volterra Integral and Related Functional Differential Equations. Cambridge Monographs on Applied and Computational Mathematics, vol. 15. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  5. Cai, H.: Legendre–Galerkin methods for third kind VIEs and CVIEs. J. Sci. Comput. 83(1), Paper No. 3, 18 (2020)

  6. Diogo, T.: Collocation and iterated collocation methods for a class of weakly singular Volterra integral equations. J. Comput. Appl. Math. 229(2), 363–372 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Diogo, T., McKee, S., Tang, T.: A Hermite-type collocation method for the solution of an integral equation with a certain weakly singular kernel. IMA J. Numer. Anal. 11(4), 595–605 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  8. Diogo, T., Franco, N.B., Lima, P.: High order product integration methods for a Volterra integral equation with logarithmic singular kernel. Commun. Pure Appl. Anal. 3(2), 217–235 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  9. Evans, G.C.: Volterra’s integral equation of the second kind, with discontinuous kernel. Trans. Am. Math. Soc. 11(4), 393–413 (1910)

    MathSciNet  MATH  Google Scholar 

  10. Fényes, T.: On the operational solution of a convolution type integral equation of the third kind. Studia Sci. Math. Hungar. 12(1-2), 65–75 (1980) (1977)

  11. Grandits, P.: A regularity theorem for a Volterra integral equation of the third kind. J. Integral Equ. Appl. 20(4), 507–526 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Han, W.: Existence, uniqueness and smoothness results for second-kind Volterra equations with weakly singular kernels. J. Integral Equ. Appl. 6(3), 365–384 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hou, D., Lin, Y., Azaiez, M., Xu, C.: A Müntz-collocation spectral method for weakly singular Volterra integral equations. J. Sci. Comput. 81(3), 2162–2187 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  14. Hu, Q.: Superconvergence of numerical solutions to Volterra integral equations with singularities. SIAM J. Numer. Anal. 34(5), 1698–1707 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  15. Imanaliev, M.I., Asanov, A.: Regularization and uniqueness of solutions of systems of nonlinear Volterra integral equations of the third kind. Dokl. Akad. Nauk 415(1), 14–17 (2007)

    MathSciNet  MATH  Google Scholar 

  16. Lima, P., Diogo, T.: An extrapolation method for a Volterra integral equation with weakly singular kernel. pp. 131–148 (1997). Volterra centennial (Tempe, AZ, 1996)

  17. Ma, X., Huang, C.: Recovery of high order accuracy in spectral collocation method for linear Volterra integral equations of the third-kind with non-smooth solutions. J. Comput. Appl. Math. 392(113458), 15 (2021)

    MathSciNet  MATH  Google Scholar 

  18. Ma, Z., Alikhanov, A.A., Huang, C., Zhang, G.: A multi-domain spectral collocation method for Volterra integral equations with a weakly singular kernel. Appl. Numer. Math. 167, 218–236 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  19. Pereverzev, S.V., Prössdorf, S.: A discretization of Volterra integral equations of the third kind with weakly singular kernels. J. Inverse Ill-Posed Probl. 5(6), 565–577 (1998) (1997)

  20. Shayanfard, F., Laeli Dastjerdi, H., Maalek Ghaini, F.M.: A numerical method for solving Volterra integral equations of the third kind by multistep collocation method. Comput. Appl. Math. 38(4), Paper No. 174, 13 (2019)

  21. Sheng, C., Wang, Z., Guo, B.: A multistep Legendre-Gauss spectral collocation method for nonlinear Volterra integral equations. SIAM J. Numer. Anal. 52(4), 1953–1980 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Song, H., Yang, Z., Brunner, H.: Analysis of collocation methods for nonlinear Volterra integral equations of the third kind. Calcolo 56(1), Paper No. 7, 29 (2019)

  23. Vainikko, G.: Cordial Volterra integral equations 1. Numer. Funct. Anal. Optim. 30(9–10), 1145–1172 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Vainikko, G.: Cordial Volterra integral equations 2. Numer. Funct. Anal. Optim. 31(1–3), 191–219 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Vainikko, G.: Spline collocation for cordial Volterra integral equations. Numer. Funct. Anal. Optim. 31(1–3), 313–338 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  26. Vainikko, G.: Spline collocation-interpolation method for linear and nonlinear cordial Volterra integral equations. Numer. Funct. Anal. Optim. 32(1), 83–109 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Wang, Z., Zhou, M., Guo, Y.: An hp-version Jacobi spectral collocation method for the third-kind VIEs. J. Sci. Comput. 87(1), Paper No. 19, 15 (2021)

Download references

Acknowledgements

The authors would like to thank the editor and the anonymous referees for their valuable suggestions and comments.

Funding

This work was supported by National Natural Science Foundation of China (Nos. 12171177 and 12011530058).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, 430074, China

    Zheng Ma & Chengming Huang

  2. Hubei Key Laboratory of Engineering Modeling and Scientific Computing, Huazhong University of Science and Technology, Wuhan, 430074, China

    Chengming Huang

Authors
  1. Zheng Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chengming Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chengming Huang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, Z., Huang, C. Fractional Collocation Method for Third-Kind Volterra Integral Equations with Nonsmooth Solutions. J Sci Comput 95, 26 (2023). https://doi.org/10.1007/s10915-023-02155-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02155-z

Keywords

Mathematics Subject Classification

Search

Navigation