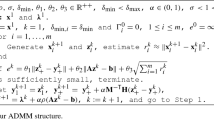Fast Alternating Direction Multipliers Method by Generalized Krylov Subspaces | Journal of Scientific Computing Skip to main content
Springer Nature Link
Log in

Fast Alternating Direction Multipliers Method by Generalized Krylov Subspaces

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

The Alternating Direction Multipliers Method (ADMM) is a very popular and powerful algorithm for the solution of many optimization problems. In the recent years it has been widely used for the solution of ill-posed inverse problems. However, one of its drawback is the possibly high computational cost, since at each iteration, it requires the solution of a large-scale least squares problem. In this work we propose a computationally attractive implementation of ADMM, with particular attention to ill-posed inverse problems. We significantly decrease the computational cost by projecting the original large scale problem into a low-dimensional subspace by means of Generalized Krylov Subspaces (GKS). The dimension of the projection space is not an additional parameter of the method as it increases with the iterations. The construction of GKS allows for very fast computations, regardless of the increasing size of the problem. Several computed examples show the good performances of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Almeida, M.S., Figueiredo, M.: Deconvolving images with unknown boundaries using the alternating direction method of multipliers. IEEE Trans. Image Process. 22(8), 3074–3086 (2013)

    Article  MathSciNet  Google Scholar 

  2. Almeida, M.S., Figueiredo, M.A.: Blind image deblurring with unknown boundaries using the alternating direction method of multipliers. In: Proceedings of the 2013 IEEE International Conference on Image Processing, pp. 586–590. IEEE (2013)

  3. Almeida, M.S., Figueiredo, M.A.: Frame-based image deblurring with unknown boundary conditions using the alternating direction method of multipliers. In: Proceedings of the 2013 IEEE International Conference on Image Processing, pp. 582–585. IEEE (2013)

  4. Bentbib, A.H., El Guide, M., Jbilou, K.: A generalized matrix Krylov subspace method for TV regularization. J. Comput. Appl. Math. 373, 112405 (2020)

    Article  MathSciNet  Google Scholar 

  5. Björck, Å.: Numerical methods for least squares problems. Siam (1996)

  6. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011)

    Article  Google Scholar 

  7. Buccini, A., De la Cruz Cabrera, O., Donatelli, M., Martinelli, A., Reichel, L.: Large-scale regression with non-convex loss and penalty. Appl. Numer. Math. 157, 590–601 (2020)

    Article  MathSciNet  Google Scholar 

  8. Buccini, A., De la Cruz Cabrera, O., Koukouvinos, C., Mitrouli, M., Reichel, L.: Variable selection in saturated and supersaturated designs via-minimization. Commun. Stat. Simul. Comput. pp. 1–22 (2021)

  9. Buccini, A., Dell’Acqua, P., Donatelli, M.: A general framework for ADMM acceleration. Numer. Algorithms 85, 829–848 (2020)

  10. Buccini, A., Donatelli, M., Ramlau, R.: A semiblind regularization algorithm for inverse problems with application to image deblurring. SIAM J. Sci. Comput. 40(1), A452–A483 (2018)

    Article  MathSciNet  Google Scholar 

  11. Buccini, A., Park, Y., Reichel, L.: Numerical aspects of the nonstationary modified linearized Bregman algorithm. Appl. Math. Comput. 337, 386–398 (2018)

    MathSciNet  MATH  Google Scholar 

  12. Buccini, A., Pasha, M., Reichel, L.: Linearized Krylov subspace Bregman iteration with nonnegativity constraint. Numer. Algorithms In press, 1–24 (2020)

  13. Buccini, A., Pasha, M., Reichel, L.: Modulus-based iterative methods for constrained \(\ell _p-\ell _q\) minimization. Inverse Prob. 36(8), 084001 (2020)

    Article  Google Scholar 

  14. Buccini, A., Reichel, L.: An \(\ell ^2-\ell ^q\) regularization method for large discrete ill-posed problems. J. Sci. Comput. 78(3), 1526–1549 (2019)

    Article  MathSciNet  Google Scholar 

  15. Buccini, A., Reichel, L.: An \(\ell _p-\ell _q\) minimization method with cross-validation for the restoration of impulse noise contaminated images. J. Comput. Appl. Math. p. 112824 (2020)

  16. Buccini, A., Reichel, L.: Generalized cross validation for \(\ell ^p - \ell ^q\) minimization. Numer. Algorithms 88(4), 1595–1616 (2021)

  17. Buzug, T.M.: Computed tomography. In: Kramme, R., Hoffmann, K.P., Pozos, R.S. (eds.) Springer Handbook of Medical Technology, pp. 311–342. Springer, Berlin, Heidelberg (2011)

    Chapter  Google Scholar 

  18. Cai, J.F., Chan, R.H., Shen, L., Shen, Z.: Simultaneously inpainting in image and transformed domains. Numer. Math. 112(4), 509–533 (2009)

    Article  MathSciNet  Google Scholar 

  19. Cai, J.F., Osher, S., Shen, Z.: Linearized Bregman iterations for compressed sensing. Math. Comput. 78(267), 1515–1536 (2009)

    Article  MathSciNet  Google Scholar 

  20. Cai, J.F., Osher, S., Shen, Z.: Split Bregman methods and frame based image restoration. Multiscale Model. Simul. 8(2), 337–369 (2010)

    Article  MathSciNet  Google Scholar 

  21. Chan, R.H., Liang, H.X.: Half-quadratic algorithm for \(\ell _p-\ell _q\) problems with applications to TV-\(\ell _1\) image restoration and compressive sensing. In: Efficient algorithms for global optimization methods in computer vision, pp. 78–103. Springer (2014)

  22. Daniel, J.W., Gragg, W.B., Kaufman, L., Stewart, G.W.: Reorthogonalization and stable algorithms for updating the gram-schmidt qr factorization. Math. Comput. 30(136), 772–795 (1976)

    MathSciNet  MATH  Google Scholar 

  23. Donatelli, M., Huckle, T., Mazza, M., Sesana, D.: Image deblurring by sparsity constraint on the fourier coefficients. Numer. Algorithms 72(2), 341–361 (2016)

    Article  MathSciNet  Google Scholar 

  24. Eldén, L.: Algorithms for the regularization of ill-conditioned least squares problems. BIT Numer. Math. 17(2), 134–145 (1977)

    Article  MathSciNet  Google Scholar 

  25. Engl, H.W., Hanke, M., Neubauer, A.: Regularization of inverse problems, vol. 375. Springer, New York (1996)

    Book  Google Scholar 

  26. Estatico, C., Gratton, S., Lenti, F., Titley-Peloquin, D.: A conjugate gradient like method for p-norm minimization in functional spaces. Numer. Math. 137(4), 895–922 (2017)

    Article  MathSciNet  Google Scholar 

  27. Gazzola, S., Hansen, P.C., Nagy, J.G.: IR Tools: a MATLAB package of iterative regularization methods and large-scale test problems. Numer. Algorithms 81(3), 773–811 (2019)

    Article  MathSciNet  Google Scholar 

  28. Goldstein, T., O’Donoghue, B., Setzer, S., Baraniuk, R.: Fast alternating direction optimization methods. SIAM J. Imag. Sci. 7(3), 1588–1623 (2014)

  29. Golub, G.H., Heath, M., Wahba, G.: Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 21(2), 215–223 (1979)

    Article  MathSciNet  Google Scholar 

  30. Golub, G.H., Van Loan, C.F.: Matrix computations, vol. 3. JHU press (2013)

  31. Hanke, M., Hansen, P.C.: Regularization methods for large-scale problems. Surv. Math. Ind. 3(4), 253–315 (1993)

    MathSciNet  MATH  Google Scholar 

  32. Hansen, P.C.: Rank deficient and discrete Ill-posed problems: numerical aspects of linear inversion. SIAM (1998)

  33. Hansen, P.C., Jørgensen, J.S.: Air tools II: algebraic iterative reconstruction methods, improved implementation. Numer. Algorithms 79(1), 107–137 (2018)

    Article  MathSciNet  Google Scholar 

  34. Hansen, P.C., Nagy, J.G., O’Leary, D.P.: Deblurring Images: Matrices, Spectra, and Filtering. SIAM, Philadelphia (2006)

  35. Huang, G., Lanza, A., Morigi, S., Reichel, L., Sgallari, F.: Majorization-minimization generalized Krylov subspace methods for \(\ell _p-\ell _q\) optimization applied to image restoration. BIT Numer. Math. 57(2), 351–378 (2017)

    Article  Google Scholar 

  36. Lampe, J., Reichel, L., Voss, H.: Large-scale Tikhonov regularization via reduction by orthogonal projection. Linear Algebra Appl. 436(8), 2845–2865 (2012)

    Article  MathSciNet  Google Scholar 

  37. Lanza, A., Morigi, S., Reichel, L., Sgallari, F.: A generalized Krylov subspace method for \(\ell _p-\ell _q\) minimization. SIAM J. Sci. Comput. 37(5), S30–S50 (2015)

    Article  Google Scholar 

  38. Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Phys. D 60(1–4), 259–268 (1992)

    Article  MathSciNet  Google Scholar 

  39. Stone, M.: Cross-validatory choice and assessment of statistical predictions. J. Roy. Stat. Soc. Ser. B (Methodol.) 36(2), 111–133 (1974)

    MathSciNet  MATH  Google Scholar 

  40. Weisberg, S.: Applied linear regression, vol. 528. Wiley, Hoboken (2005)

    Book  Google Scholar 

  41. Yun, J.D., Yang, S.: ADMM in Krylov subspace and its application to total variation restoration of spatially variant blur. SIAM J. Imag. Sci. 10(2), 484–507 (2017)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author would like to thank Prof. Marco Donatelli, Prof. Lothar Reichel, and the two anonimous referees for the precious comments that greatly improved the quality of this paper. The author is a member of the GNCS-INdAM. and his research is partially supported by the Regione Autonoma della Sardegna research project “Algorithms and Models for Imaging Science [AMIS]” (RASSR57257, intervento finanziato con risorse FSC 2014-2020 - Patto per lo Sviluppo della Regione Sardegna).

Author information

Authors and Affiliations

  1. Dipartimento di Matematica e Informatica, Università degli Studi di Cagliari, Via Ospedale 72, Cagliari, 09124, Italy

    Alessandro Buccini

Authors
  1. Alessandro Buccini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alessandro Buccini.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buccini, A. Fast Alternating Direction Multipliers Method by Generalized Krylov Subspaces. J Sci Comput 90, 60 (2022). https://doi.org/10.1007/s10915-021-01727-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-021-01727-1

Keywords

Mathematics Subject Classification

Search

Navigation