Generalized Exponential Time Differencing Schemes for Stiff Fractional Systems with Nonsmooth Source Term | Journal of Scientific Computing
Skip to main content
Springer Nature Link
Log in

Generalized Exponential Time Differencing Schemes for Stiff Fractional Systems with Nonsmooth Source Term

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

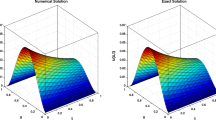
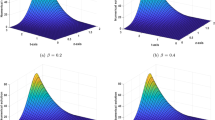
Many processes in science and engineering are described by fractional systems which may in general be stiff and involve a nonsmooth source term. In this paper, we develop robust first, second, and third order accurate exponential time differencing schemes for solving such systems. Rather than imposing regularity requirements on the solution to account for the singularity caused by the fractional derivative, we only consider regularity requirements on the source term for preserving the optimal order of accuracy of the proposed schemes. Optimal convergence rates are proved for both smooth and nonsmooth source terms using uniform and graded meshes, respectively. For efficient implementation, high-order global Padé approximations together with their fractional decompositions are developed for Mittag–Leffler functions. We present numerical experiments involving a typical stiff system, a fractional two-compartment pharmacokinetics model, a two-term fractional Kelvin–Viogt model of viscoelasticity, and a large system obtained by spatial discretization of a sub-diffusion problem. Demonstrations of the efficiency of the rational approximation implementation technique and the newly constructed high-order schemes are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Beylkin, G., Keiser, J.M., Vozovoi, L.: A new class of time discretization schemes for the solution of nonlinear PDEs. J. Comput. Phys. 147(2), 362–387 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  2. Cao, W., Zeng, F., Zhang, Z., Karniadakis, G.E.: Implicit–explicit difference schemes for nonlinear fractional differential equations with nonsmooth solutions. SIAM J. Sci. Comput. 38(5), A3070–A3093 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  3. Chikriy, A.A., Matichin, I.I.: Presentation of solutions of linear systems with fractional derivatives in the sense of Riemann–Liouville, Caputo, and Miller–Ross. J. Autom. Inform. Sci. 40, 1–11 (2008)

    Google Scholar 

  4. Cox, S.M., Matthews, P.C.: Exponential time differencing for stiff systems. J. Comput. Phys. 176(2), 430–455 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  5. Di Paola, M., Pinnola, F.P., Zingales, M.: Fractional differential equations and related exact mechanical models. Comput. Math. Appl. 66(5), 608–620 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, Berlin (2010)

    Book  MATH  Google Scholar 

  7. Furati, K.M., Yousuf, M., Khaliq, A.: Fourth-order methods for space fractional reaction–diffusion equations with non-smooth data. Int. J. Comput. Math. 95(6–7), 1240–1256 (2018)

    Article  MathSciNet  Google Scholar 

  8. Garappa, R., Popolizio, M.: Generalized exponential time differencing methods for fractional order problems. Comput. Math. Appl. 62, 876–890 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Garrappa, R.: Exponential integrators for time-fractional partial differential equations. Eur. Phys. J. Spec. Top. 222(8), 1915–1927 (2013)

    Article  Google Scholar 

  10. Garrappa, R.: Numerical evaluation of two and three parameter Mittag–Leffler functions. SIAM J. Numer. Anal. 53(3), 1350–1369 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  11. Garrappa, R., Popolizio, M.: Computing the matrix Mittag–Leffler function with applications to fractional calculus. J. Sci. Comput. 77(1), 129–153 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  12. Garrappa, R., Moret, I., Popolizio, M.: On the time-fractional Schrödinger equation: theoretical analysis and numerical solution by matrix Mittag–Leffler functions. Comput. Math. Appl. 74(5), 977–992 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  13. Gorenflo, R., Loutchko, J., Luchko, Y.: Computation of the Mittag–Leffler function \(E_{\alpha,\beta }(z)\) and its derivative. Fract. Cal. Appl. Anal. 5(4), 491–518 (2002)

    MathSciNet  Google Scholar 

  14. Hochbruck, M., Ostermann, A.: Exponential integrators. Acta Numer. 19, 209–286 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  15. Ionescu, C., Lopes, A., Copot, D., Machado, J., Bates, J.: The role of fractional calculus in modeling biological phenomena: a review. Commun. Nonlinear Sci. Numer. Simul. 51, 141–159 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kaur, A., Takhar, P.S., Smith, D., Mann, J., Brashears, M.: Fractional differential equations based modeling of microbial survival and growth curves: model development and experimental validation. J. Food Sci. 73(8), E403–E414 (2008)

    Article  Google Scholar 

  17. Kilbas, A., Srivastava, H., Trujullo, J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    Google Scholar 

  18. McLean, W., Mustapha, K.: A second-order accurate numerical method for a fractional wave equation. Numer. Math. 105(3), 481–510 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  19. Minchev, B., Wright, W.: A review of exponential integrators for first order semi-linear problems. Technical Report 2/05, Department of Mathematics, NTNU (2005)

  20. Prakash, B., Setia, A., Bose, S.: Numerical solution for a system of fractional differential equations with applications in fluid dynamics and chemical engineering. Int. J. Chem. React. Eng. 15(5), 20170093 (2017)

  21. Sadeghi, A., Cardoso, J.R.: Some notes on properties of the matrix Mittag–Leffler function. Appl. Math. Comput. 338, 733–738 (2018)

    MathSciNet  MATH  Google Scholar 

  22. Sarumi, I.O., Furati, K.M., Khaliq, A.Q.M.: Highly accurate global Padé approximations of generalized Mittag–Leffler function and its inverse. J. Sci. Comput. 82, 46 (2020)

  23. Shimizu, N., Zhang, W.: Fractional calculus approach to dynamic problems of viscoelastic materials. JSME Int. J. Ser. C 42(4), 825–837 (1999)

    Article  Google Scholar 

  24. Sopasakis, P., Sarimveis, H., Macheras, P., Dokoumetzidis, A.: Fractional calculus in pharmacokinetics. J. Pharmacokinet. Pharmacodyn. 45(1), 107–125 (2018)

    Article  Google Scholar 

  25. Stynes, M.: Singularities. In: Handbook of Fractional Calculus with Applications: Numerical Methods, vol. 3. De Gruyter, Berlin, pp. 287–305 (2019)

  26. Stynes, M.: Too much regularity may force too much uniqueness. Fract. Cal. Appl. Anal. 19(6), 1554–1562 (2016)

    MathSciNet  MATH  Google Scholar 

  27. Torvik, P.J., Bagley, D.: Fractional derivatives in the description of damping materials and phenomena. Role Damp. Vib. Noise Control 5, 125–135 (1987)

    Google Scholar 

  28. Veber, V.K.: Linear equations with fractional derivatives and constant coefficients in spaces of generalized functions. In: Studies in integro-differential equations, number 18, pp. 306–312. Frunze, Ilim (1985) (in Russian)

  29. Veber, V.K.: On the general theory of linear systems with fractional derivatives. In: Studies in Integro-Differential Equations, number 18, pp. 301–305. Frunze, Ilim (1985) (in Russian)

  30. Zeng, F., Li, C., Liu, F., Turner, I.: Numerical algorithms for time-fractional subdiffusion equation with second-order accuracy. SIAM J. Sci. Comput. 37(1), A55–A78 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge the support provided by the Deanship of Scientific Research at King Fahd University of Petroleum and Minerals via the Project SB191001. We thank the anonymous reviewers for their valuable suggestions and comments.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, King Fahd University of Petroleum and Minerals, Dhahran, 31261, Saudi Arabia

    Ibrahim O. Sarumi, Khaled M. Furati & Kassem Mustapha

  2. Department of Mathematical Sciences, Middle Tennessee State University, Murfreesboro, TN, 37132-0001, USA

    Abdul Q. M. Khaliq

Authors
  1. Ibrahim O. Sarumi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Khaled M. Furati
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abdul Q. M. Khaliq
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Kassem Mustapha
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Khaled M. Furati.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sarumi, I.O., Furati, K.M., Khaliq, A.Q.M. et al. Generalized Exponential Time Differencing Schemes for Stiff Fractional Systems with Nonsmooth Source Term. J Sci Comput 86, 23 (2021). https://doi.org/10.1007/s10915-020-01374-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01374-y

Keywords

Search

Navigation