Numerical Approximation of a Phase-Field Surfactant Model with Fluid Flow | Journal of Scientific Computing Skip to main content
Springer Nature Link
Log in

Numerical Approximation of a Phase-Field Surfactant Model with Fluid Flow

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

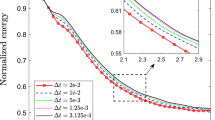
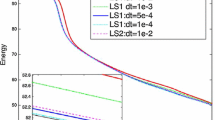
Modeling interfacial dynamics with soluble surfactants in a multiphase system is a challenging task. Here, we consider the numerical approximation of a phase-field surfactant model with fluid flow. The nonlinearly coupled model consists of two Cahn–Hilliard-type equations and incompressible Navier–Stokes equation. With the introduction of two auxiliary variables, the governing system is transformed into an equivalent form, which allows the nonlinear potentials to be treated efficiently and semi-explicitly. By certain subtle explicit-implicit treatments to stress and convective terms, we construct first and second-order time marching schemes, which are extremely efficient and easy-to-implement, for the transformed governing system. At each time step, the schemes involve solving only a sequence of linear elliptic equations, and computations of phase-field variables, velocity and pressure are fully decoupled. We further establish a rigorous proof of unconditional energy stability for the first-order scheme. Numerical results in both two and three dimensions are obtained, which demonstrate that the proposed schemes are accurate, efficient and unconditionally energy stable. Using our schemes, we investigate the effect of surfactants on droplet deformation and collision under a shear flow, where the increase of surfactant concentration can enhance droplet deformation and inhibit droplet coalescence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Khatri, S., Tornberg, A.-K.: An embedded boundary method for soluble surfactants with interface tracking for two-phase flows. J. Comput. Phys. 256, 768–790 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  2. Yang, X.: Numerical approximations for the Cahn–Hilliard phase field model of the binary fluid-surfactant system. J. Sci. Comput. 1–21 (2017)

  3. Yang, X., Ju, L.: Linear and unconditionally energy stable schemes for the binary fluid–surfactant phase field model. Comput. Methods Appl. Mech. Eng. 318, 1005–1029 (2017)

    Article  MathSciNet  Google Scholar 

  4. Fonseca, I., Morini, M., Slastikov, V.: Surfactants in foam stability: a phase-field model. Arch. Ration. Mech. Anal. 183, 411–456 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. Iglauer, S., Wu, Y., Shuler, P., Tang, Y., Goddard III, W.A.: New surfactant classes for enhanced oil recovery and their tertiary oil recovery potential. J. Petrol. Sci. Eng. 71, 23–29 (2010)

    Article  Google Scholar 

  6. Liu, H., Zhang, Y.: Phase-field modeling droplet dynamics with soluble surfactants. J. Comput. Phys. 229, 9166–9187 (2010)

    Article  MATH  Google Scholar 

  7. Lai, M.-C., Tseng, Y.-H., Huang, H.: Numerical simulation of moving contact lines with surfactant by immersed boundary method. Commun. Comput. Phys. 8, 735 (2010)

    MATH  Google Scholar 

  8. Liu, H., Ba, Y., Wu, L., Li, Z., Xi, G., Zhang, Y.: A hybrid lattice Boltzmann and finite difference method for droplet dynamics with insoluble surfactants. J. Fluid Mech. 837, 381–412 (2018)

    Article  MathSciNet  Google Scholar 

  9. Jacqmin, D.: Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 155, 96–127 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  10. Shen, J., Yang, X.: A phase-field model and its numerical approximation for two-phase incompressible flows with different densities and viscosities. SIAM J. Sci. Comput. 32, 1159–1179 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Shen, J., Yang, X.: Numerical approximations of Allen–Cahn and Cahn–Hilliard equations. Discrete Contin. Dyn. Syst 28, 1669–1691 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  12. Shen, J., Yang, X.: Decoupled, energy stable schemes for phase-field models of two-phase incompressible flows. SIAM J. Numer. Anal. 53, 279–296 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. James, A.J., Lowengrub, J.: A surfactant-conserving volume-of-fluid method for interfacial flows with insoluble surfactant. J. Comput. Phys. 201, 685–722 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  14. Muradoglu, M., Tryggvason, G.: A front-tracking method for computation of interfacial flows with soluble surfactants. J. Comput. Phys. 227, 2238–2262 (2008)

    Article  MATH  Google Scholar 

  15. Zhang, L., Kang, Q., Yao, J., Gao, Y., Sun, Z., Liu, H., Valocchi, A.J.: Pore scale simulation of liquid and gas two-phase flow based on digital core technology. Sci. China Technol. Sci. 58, 1375–1384 (2015)

    Article  Google Scholar 

  16. Booty, M., Siegel, M.: A hybrid numerical method for interfacial fluid flow with soluble surfactant. J. Comput. Phys. 229, 3864–3883 (2010)

    Article  MATH  Google Scholar 

  17. Xu, J.-J., Ren, W.: A level-set method for two-phase flows with moving contact line and insoluble surfactant. J. Comput. Phys. 263, 71–90 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Zhang, Z., Xu, S., Ren, W.: Derivation of a continuum model and the energy law for moving contact lines with insoluble surfactants. Phys. Fluids 26, 062103 (2014)

    Article  Google Scholar 

  19. Xu, J.-J., Li, Z., Lowengrub, J., Zhao, H.: A level-set method for interfacial flows with surfactant. J. Comput. Phys. 212, 590–616 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  20. Xu, J.-J., Yang, Y., Lowengrub, J.: A level-set continuum method for two-phase flows with insoluble surfactant. J. Comput. Phys. 231, 5897–5909 (2012)

    Article  MathSciNet  Google Scholar 

  21. Kou, J., Sun, S.: Thermodynamically consistent modeling and simulation of multi-component two-phase flow with partial miscibility. Comput. Methods Appl. Mech. Eng. 331, 623–649 (2018)

    Article  MathSciNet  Google Scholar 

  22. Zhu, G., Yao, J., Li, A., Sun, H., Zhang, L.: Pore-scale investigation of carbon dioxide-enhanced oil recovery. Energy Fuels 31, 5324–5332 (2017)

    Article  Google Scholar 

  23. Tóth, G.I., Kvamme, B.: Analysis of Ginzburg–Landau-type models of surfactant-assisted liquid phase separation. Phys. Rev. E 91, 032404 (2015)

    Article  Google Scholar 

  24. Teng, C.-H., Chern, I.-L., Lai M.-C.: Simulating binary fluid-surfactant dynamics by a phase field model. Discrete and Continuous Dynamical Systems-Series B, Special issue for FAN2010 in honor of J. Thomas Beale (in press) (2012)

  25. Yu, H., Yang, X.: Numerical approximations for a phase-field moving contact line model with variable densities and viscosities. J. Comput. Phys. 334, 665–686 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  26. Yue, P., Feng, J.J., Liu, C., Shen, J.: A diffuse-interface method for simulating two-phase flows of complex fluids. J. Fluid Mech. 515, 293–317 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  27. Kou, J., Sun, S.: An adaptive finite element method for simulating surface tension with the gradient theory of fluid interfaces. J. Comput. Appl. Math. 255, 593–604 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Zhu, G., Chen, H., Yao, J., Sun, S.: Efficient energy stable schemes for the hydrodynamics coupled phase-field model. Appl. Math. Model. 70, 82 (2018)

    Article  MathSciNet  Google Scholar 

  29. Laradji, M., Guo, H., Grant, M., Zuckermann, M.J.: The effect of surfactants on the dynamics of phase separation. J. Phys. Condens. Matter 4, 6715 (1992)

    Article  Google Scholar 

  30. Komura, S., Kodama, H.: Two-order-parameter model for an oil-water-surfactant system. Phys. Rev. E 55, 1722 (1997)

    Article  Google Scholar 

  31. Theissen, O., Gompper, G.: Lattice–Boltzmann study of spontaneous emulsification. Eur. Phys. J. B Condens. Matter Complex Syst. 11, 91–100 (1999)

    Article  Google Scholar 

  32. Van der Sman, R., Van der Graaf, S.: Diffuse interface model of surfactant adsorption onto flat and droplet interfaces. Rheol. Acta 46, 3–11 (2006)

    Article  Google Scholar 

  33. Zhu, G., Kou, J., Sun, S., Yao, J., Li, A.: Decoupled, energy stable schemes for a phase-field surfactant model. Comput. Phys. Commun. 233, 67 (2018)

    Article  MathSciNet  Google Scholar 

  34. Engblom, S., Do-Quang, M., Amberg, G., Tornberg, A.-K.: On diffuse interface modeling and simulation of surfactants in two-phase fluid flow. Commun. Computat. Phys. 14, 879–915 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  35. Garcke, H., Lam, K.F., Stinner, B.: Diffuse interface modelling of soluble surfactants in two-phase flow (2013). arXiv preprint arXiv:1303.2559

  36. Pätzold, G., Dawson, K.: Numerical simulation of phase separation in the presence of surfactants and hydrodynamics. Phys. Rev. E 52, 6908 (1995)

    Article  Google Scholar 

  37. Teigen, K.E., Song, P., Lowengrub, J., Voigt, A.: A diffuse-interface method for two-phase flows with soluble surfactants. J. Comput. Phys. 230, 375–393 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  38. Gu, S., Zhang, H., Zhang, Z.: An energy-stable finite-difference scheme for the binary fluid-surfactant system. J. Comput. Phys. 270, 416–431 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  39. Yun, A., Li, Y., Kim, J.: A new phase-field model for a water–oil-surfactant system. Appl. Math. Comput. 229, 422–432 (2014)

    MathSciNet  MATH  Google Scholar 

  40. Yang, X., Ju, L.: Efficient linear schemes with unconditional energy stability for the phase field elastic bending energy model. Comput. Methods Appl. Mech. Eng. 315, 691–712 (2017)

    Article  MathSciNet  Google Scholar 

  41. Yang, X., Zhao, J., Wang, Q., Shen, J.: Numerical approximations for a three-component Cahn–Hilliard phase-field model based on the invariant energy quadratization method. Math. Models Methods Appl. Sci. 27, 1993–2030 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  42. Alpak, F.O., Riviere, B., Frank, F.: A phase-field method for the direct simulation of two-phase flows in pore-scale media using a non-equilibrium wetting boundary condition. Comput. Geosci. 20, 881–908 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  43. Frank, F., Liu, C., Alpak, F.O., Berg, S., Riviere, B.: Direct numerical simulation of flow on pore-scale images using the phase-field method. SPE J. (2018)

  44. Zhu, G., Yao, J., Sun, H., Zhang, M., Xie, M., Sun, Z., Tao, L.: The numerical simulation of thermal recovery based on hydraulic fracture heating technology in shale gas reservoir. J. Nat. Gas. Sci. Eng. 28, 305–316 (2016)

    Article  Google Scholar 

  45. Liu, C., Shen, J.: A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method. Phys. D 179, 211–228 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  46. Yang, X., Yu, H.: Linear, second order and unconditionally energy stable schemes for a phase-field moving contact line model (2017). arXiv preprint arXiv:1703.01311

  47. Gao, M., Wang, X.-P.: A gradient stable scheme for a phase field model for the moving contact line problem. J. Comput. Phys. 231, 1372–1386 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  48. Bao, K., Shi, Y., Sun, S., Wang, X.-P.: A finite element method for the numerical solution of the coupled Cahn–Hilliard and Navier–Stokes system for moving contact line problems. J. Comput. Phys. 231, 8083–8099 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  49. Kou, J., Sun, S.: Thermodynamically consistent simulation of nonisothermal diffuse-interface two-phase flow with Peng–Robinson equation of state. J. Comput. Phys. 371, 581–605 (2018)

    Article  MathSciNet  Google Scholar 

  50. Kou, J., Sun, S., Wang, X.: Linearly decoupled energy-stable numerical methods for multicomponent two-phase compressible flow. SIAM J. Numer. Anal. 56, 3219–3248 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  51. Copetti, M., Elliott, C.M.: Numerical analysis of the Cahn–Hilliard equation with a logarithmic free energy. Numer. Math. 63, 39–65 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  52. Shen, J., Xu, J., Yang, J.: The scalar auxiliary variable (SAV) approach for gradient flows. J. Comput. Phys. 353, 407–416 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  53. Cheng, Q., Shen, J., Yang, X.: Highly efficient and accurate numerical schemes for the epitaxial thin film growth models by using the SAV approach. J. Sci. Comput. 1–21 (2018)

  54. Fjordholm, U.S., Mishra, S., Tadmor, E.: Well-balanced and energy stable schemes for the shallow water equations with discontinuous topography. J. Comput. Phys. 230, 5587–5609 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  55. Shen, J., Yang, X.: Decoupled energy stable schemes for phase-field models of two-phase complex fluids. SIAM J. Sci. Comput. 36, B122–B145 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  56. Chen, W., Wang, C., Wang, X., Wise, S.M.: A positivity-preserving, energy stable numerical scheme for the Cahn–Hilliard equation with logarithmic potential (2017). arXiv preprint arXiv:1712.03225

  57. Chen, W., Feng, W., Zhang, L., Cui, C., Ma, X., Sun, Z., Liu, F., Zhang, K.: A fractal discrete fracture network model for history matching of naturally fractured reservoirs. Fractals 27, 1940008 (2018)

    MathSciNet  Google Scholar 

  58. Diegel, A.E., Wang, C., Wang, X., Wise, S.M.: Convergence analysis and error estimates for a second order accurate finite element method for the Cahn–Hilliard–Navier–Stokes system. Numer. Math. 137, 495–534 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  59. Feng, X., He, Y., Liu, C.: Analysis of finite element approximations of a phase field model for two-phase fluids. Math. Comput. 76, 539–571 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  60. Li, J., Yu, B., Wang, Y., Tang, Y., Wang, H.: Study on computational efficiency of composite schemes for convection–diffusion equations using single-grid and multigrid methods. J. Therm. Sci. Technol. 10, JTST0009–JTST0009 (2015)

    Article  Google Scholar 

  61. F. Moukalled, L. Mangani, M. Darwish, The finite volume method in computational fluid dynamics. An advanced introduction with OpenFOAM and Matlab, pp. 3–8 (2016)

Download references

Acknowledgements

Jun Yao and Guangpu Zhu acknowledge that this work is supported by the National Science and Technology Major Project (2016ZX05011-001), the NSF of China (51804325, 51504276, and 51674280). The work of Shuyu Sun and Jisheng Kou is supported by the KAUST research fund awarded to the Computational Transport Phenomena Laboratory at KAUST through the Grant BAS/1/1351-01-01.

Author information

Authors and Affiliations

  1. Research Center of Multiphase Flow in Porous Media, School of Petroleum Engineering, China University of Petroleum (East China), Qingdao, 266580, China

    Guangpu Zhu, Jun Yao & Aifen Li

  2. School of Mathematics and Statistics, Hubei Engineering University, Xiaogan, 432000, Hubei, China

    Jisheng Kou

  3. Computational Transport Phenomena Laboratory, Division of Physical Science and Engineering, King Abdullah University of Science and Technology, Thuwal, 23955-6900, Kingdom of Saudi Arabia

    Shuyu Sun

Authors
  1. Guangpu Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jisheng Kou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shuyu Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jun Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Aifen Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuyu Sun.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhu, G., Kou, J., Sun, S. et al. Numerical Approximation of a Phase-Field Surfactant Model with Fluid Flow. J Sci Comput 80, 223–247 (2019). https://doi.org/10.1007/s10915-019-00934-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-019-00934-1

Keywords

Search

Navigation