A Fast Finite Difference Method for Three-Dimensional Time-Dependent Space-Fractional Diffusion Equations with Fractional Derivative Boundary Conditions | Journal of Scientific Computing
Skip to main content
Springer Nature Link
Log in

A Fast Finite Difference Method for Three-Dimensional Time-Dependent Space-Fractional Diffusion Equations with Fractional Derivative Boundary Conditions

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

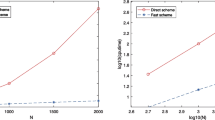
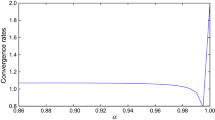
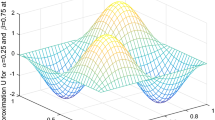
We develop a fast finite difference method for time-dependent variable-coefficient space-fractional diffusion equations with fractional derivative boundary-value conditions in three dimensional spaces. Fractional differential operators appear in both of the equation and the boundary conditions. Because of the nonlocal nature of the fractional Neumann boundary operator, the internal and boundary nodes are strongly coupled together in the coupled linear system. The stability and convergence of the finite difference method are discussed. For the implementation, the development of the fast method is based upon a careful analysis and delicate decomposition of the structure of the coefficient matrix. The fast method has approximately linear computational complexity per Krylov subspace iteration and an optimal-order memory requirement. Numerical results are presented to show the utility of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Baeumer, B., Kovcs, M., Meerschaert, M., Schilling, R., Straka, P.: Reflected spectrally negative stable processes and their governing equations. Trans. Am. Math. Soc. 368(1), 227–248 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  2. Benson, D.A., Wheatcraft, S.W., Meerschaert, M.M.: The fractional-order governing equation of Lévy motion. Water Resour. Res. 36(6), 1413–1423 (2000)

    Article  Google Scholar 

  3. Chan, R.H., Ng, M.K.: Conjugate gradient methods for Toeplitz systems. SIAM Rev. 38(3), 427–482 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  4. Chen, S., Liu, F., Jiang, X., Turner, I., Anh, V.: A fast semi-implicit difference method for a nonlinear two-sided space-fractional diffusion equation with variable diffusivity coefficients. Appl. Math. Comput. 257, 591–601 (2015)

    MathSciNet  MATH  Google Scholar 

  5. Chen, S., Jie, S., Wang, L.L.: Generalized Jacobi functions and their applications to fractional differential equations. Math. Comput. 85(300), 1603–1638 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cui, M.: Compact alternating direction implicit method for two-dimensional time fractional diffusion equation. J. Comput. Phys. 231(6), 2621–2633 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Deng, W.: Finite element method for the space and time fractional Fokker-Planck equation. SIAM J. Numer. Anal. 47(1), 204–226 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Du, N., Wang, H.: A fast finite element method for space-fractional dispersion equations on bounded domains in \(\mathbb{R}^2\). SIAM J. Sci. Comput. 37(3), A1614–A1635 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ervin, V.J., Roop, J.P.: Variational solution of fractional advection dispersion equations on bounded domains in \(R^d\). Numer. Methods Partial Differ. Equ. 23(2), 256–281 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Gao, G.H., Sun, Z.Z.: Two alternating direction implicit difference schemes for two-Dimensional distributed-Order fractional diffusion equations. J. Sci. Comput. 66(3), 1–32 (2015)

  11. Jia, J., Wang, H.: Fast finite difference methods for space-fractional diffusion equations with fractional derivative boundary conditions. J. Comput. Phys. 293, 359–369 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Jia, J., Wang, H.: A preconditioned fast finite volume scheme for a fractional differential equation discretized on a locally refined composite mesh. J. Comput. Phys. 299, 842–862 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Lei, S.L., Sun, H.W.: A circulant preconditioner for fractional diffusion equations. J. Comput. Phys. 242, 715–725 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Liu, F., Anh, V., Turner, I.: Numerical solution of the space fractional Fokker-Planck equation. J. Comput. Appl. Math. 166, 209–219 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lim, S.C., Teo, L.P.: Repulsive Casimir force from fractional Neumann boundary conditions. Phys. Lett. B 679(2), 130–137 (2009)

    Article  MathSciNet  Google Scholar 

  17. Lynch, V.E., Carreras, B.A., del-Castillo-Negrete, D., Ferreira-Mejias, K.M., Hicks, H.R.: Numerical methods for the solution of partial differential equations of fractional order. J. Comput. Phys. 192, 406–421 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  18. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 172, 65–77 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56(1), 80–90 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  20. Meerschaert, M.M., Scheffler, H.P., Tadjeran, C.: Finite difference methods for two-dimensional fractional dispersion equation. J. Comput. Phys. 211, 249–261 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  21. Metzler, R., Klafter, J.: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339, 1–77 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  22. Mao, Z.P., Jie, S.: Efficient spectral-Galerkin methods for fractional partial differential equations with variable coefficients. J. Comput. Phys. 307, 243–261 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  23. Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)

    MATH  Google Scholar 

  24. Sun, H.G., Chen, W., Chen, Y.Q.: Fractional differential models for anomalous diffusion. Phys. A 389, 2719–2724 (2010)

    Article  Google Scholar 

  25. Wang, H., Basu, T.S.: A fast finite difference method for two-dimensional space-fractional diffusion equations. SIAM J. Sci. Comput. 34, A2444–A2458 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang, H., Du, N.: A superfast-preconditioned iterative method for steady-state space-fractional diffusion equations. J. Comput. Phys. 240, 49–57 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  27. Wang, H., Du, N.: A fast finite difference method for three-dimensional time-dependent space-fractional diffusion equations and its efficient implementation. J. Comput. Phys. 253, 50–63 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang, H., Du, N.: Fast alternating-direction finite difference methods for three-dimensional space-fractional diffusion equations. J. Comput. Phys. 258, 305–318 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wang, H., Wang, K., Sircar, T.: A direct \(O(N\log ^2 N)\) finite difference method for fractional diffusion equations. J. Comput. Phys. 229, 8095–8104 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  30. Zeng, F.H., Mao, Z.P., Karniadakis, G.E.: A generalized spectral collocation method with tunable accuracy for fractional differential equations with end-point singularities. SIAM J. Sci. Comput. 39(1), A360–A383 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  31. Zhang, X., Lv, M., Crawford, J.W., Young, I.M.: The impact of boundary on the fractional advection-dispersion equation for solute transport in soil: defining the fractional dispersive flux with the caputo derivatives. Adv. Water Resour. 30, 1205–1217 (2007)

    Article  Google Scholar 

  32. Zhang, Y.: A finite difference method for fractional partial differential equation. Appl. Math. Comput. 215, 524–529 (2009)

    MathSciNet  MATH  Google Scholar 

  33. Zhao, X., Sun, Z.Z., Karniadakis, G.E.: Second-order approximations for variable order fractional derivatives: algorithms and applications. J. Comput. Phys. 293, 184–200 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  34. Zheng, Y., Li, C., Zhao, Z.: A note on the finite element method for the space-fractional advection diffusion equation. Comput. Math. Appl. 59, 1718–1726 (2010)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the OSD/ARO MURI Grant W911NF-15-1-0562, by the National Natural Science Foundation of China under Grants 11471194, 91630207 and 11571115, by the National Science Foundation under Grant DMS-1620194, by the National Science and technology major projects of China under Grants 2011ZX05052 and 2011ZX05011-004, by Natural Science Foundation of Shandong Province of China under Grant ZR2011AM015, by Taishan Scholars Program of Shandong Province of China, and by the China Scholarship Council (File No. 201606220127). The authors would like to express their sincere thanks to the referees for their very helpful comments and suggestions, which greatly improved the quality of this paper.

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University, Jinan, 250100, China

    Meng Zhao & Aijie Cheng

  2. Department of Mathematics, University of South Carolina, Columbia, SC, 29208, USA

    Hong Wang

Authors
  1. Meng Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aijie Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aijie Cheng.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, M., Wang, H. & Cheng, A. A Fast Finite Difference Method for Three-Dimensional Time-Dependent Space-Fractional Diffusion Equations with Fractional Derivative Boundary Conditions. J Sci Comput 74, 1009–1033 (2018). https://doi.org/10.1007/s10915-017-0478-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-017-0478-8

Keywords

Search

Navigation