Abstract
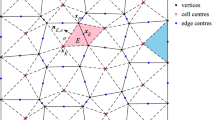
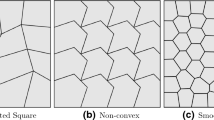
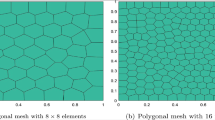
On arbitrary polygonal grids, a family of vertex-centered finite volume schemes are suggested for the numerical solution of the strongly nonlinear parabolic equations arising in radiation hydrodynamics and magnetohydrodynamics. We define the primary unknowns at the cell vertices and derive the schemes along the linearity-preserving approach. Since we adopt the same cell-centered diffusion coefficients as those in most existing finite volume schemes, it is required to introduce some auxiliary unknowns at the cell centers in the case of nonlinear diffusion coefficients. A second-order positivity-preserving algorithm is then suggested to interpolate these auxiliary unknowns via the primary ones. All the schemes lead to symmetric and positive definite linear systems and their stability can be rigorously analyzed under some standard and weak geometry assumptions. More interesting is that these vertex-centered schemes do not have the so-called numerical heat-barrier issue suffered by many existing cell-centered or hybrid schemes (Lipnikov et al. in J Comput Phys 305:111–126, 2016). Numerical experiments are also presented to show the efficiency and robustness of the schemes in simulating nonlinear parabolic problems.









Similar content being viewed by others
References
Aavatsmark, I., Barkve, T., Bøe, Ø., Mannseth, T.: Discretization on unstructured grids for inhomogeneous, anisotropic media. Part I: derivation of the methods. SIAM J. Sci. Comput. 19, 1700–1716 (1998)
Bank, R.E., Rose, D.J.: Some error estimates for the box method. SIAM J. Numer. Anal. 24, 777–787 (1987)
Basko, M.M., Maruhn, J., Tauschwitz, A.: An efficient cell-centered diffusion scheme for quadrilateral grids. J. Comput. Phys. 228, 2175–2193 (2009)
Beirao da Veiga, L., Lipnikov, K., Manzini, G.: The Mimetic Finite Difference Method for Elliptic PDEs. Springer, New York (2014)
Breil, J., Maire, P.H.: A cell-centered diffusion scheme on two-dimensional unstructured meshes. J. Comput. Phys. 224, 785–823 (2007)
Brezzi, F., Lipnikov, K., Simoncini, V.: A family of mimetic finite difference methods on polygonal and polyhedral meshes. Math. Models Methods Appl. Sci. 15, 1533–1551 (2005)
Cai, Z.: On the finite volume element method. Numer. Math. 58, 713–735 (1991)
Camier, J.S., Hermeline, F.: A monotone non-linear finite volume method for approximating diffusion operators on general meshes. Int. J. Numer. Meth. Eng. 107, 496–519 (2016)
Coudière, Y., Vila, J.-P., Villedieu, P.: Convergence rate of a finite volume scheme for a two-dimensional diffusion convection problem. Math. Model. Numer. Anal. 33, 493–516 (1999)
Droniou, J.: Finite volume schemes for diffusion equations: introduction to and review of modern methods. Math. Models Methods Appl. Sci. 24, 1575–1619 (2014)
Eymard, R., Gallouët, T., Herbin, R.: Discretization of heterogeneous and anisotropic diffusion problems on general nonconforming meshes SUSHI: a scheme using stabilization and hybrid interfaces. IMA J. Numer. Anal. 30, 1009–1043 (2010)
Eymard, R., Henry, G., Herbin, R., Hubert, F., Klöfkorn, R., Manzini, G.: 3D benchmark on discretization schemes for anisotropic diffusion problems on general grids. In: Fort, J., Furst, J., Halama, J., Herbin, R., Hubert, F. (eds.) Finite Volumes for Complex Applications VI, pp. 895–930. Springer, New York (2008)
Feng, X., Li, R., He, Y., Liu, D.: P1-nonconforming quadrilateral finite volume methods for the semilinear elliptic equations. J. Sci. Comput. 52, 519–545 (2012)
Gao, Z., Wu, J.: A linearity-preserving cell-centered scheme for the heterogeneous and anisotropic diffusion equations on general meshes. Int. J. Numer. Methods Fluids 67, 2157–2183 (2011)
Gao, Z., Wu, J.: A small stencil and extremum-preserving scheme for anisotropic diffusion problems on arbitrary 2D and 3D meshes. J. Comput. Phys. 250, 308–331 (2013)
Gao, Z., Wu, J.: A second-order positivity-preserving finite volume scheme for diffusion equations on general meshes. SIAM J. Sci. Comput. 37, A420–A438 (2015)
Guo, S., Zhang, M., Zhou, H., Zhang, S.: Improved numerical method for three dimensional diffusion equation with strongly discontinuous coefficients. High Power Laser Part. Beams 27, 092014-1–092014-6 (2015)
Herbin, R., Hubert, F.: Benchmark on discretization schemes for anisotropic diffusion problems on general grids. In: Eymard, R., Herard, J.-M. (eds.) Finite Volumes for Complex Applications V, pp. 659–692. Wiley, London (2008)
Hermeline, F.: Approximation of diffusion operators with discontinuous tensor coefficients on distorted meshes. Comput. Methods Appl. Mech. Eng. 192, 1939–1959 (2003)
Huang, W., Kappen, A.M.: A study of cell-center finite volume methods for diffusion equations. Mathematics Research Report 98-10-01, Department of Mathematics, University of Kansas, Laurence KS (1998)
Huang, Z., Li, Y.: Monotone finite point method for non-equilibrium radiation diffusion equations. BIT Numer. Math. 56, 659–679 (2016)
Irons, B. M., Razzaque, A.: Experience with the patch test for convergence of finite elements. In: Proceedings of Symposia on Mathematical Foundations of the Finite Element Method with Application to Partial Differential Operators, pp. 557–587. Academic Press, New York (1972)
Kannan, R., Springel, V., Pakmor, R., Marinacci, F., Vogelsberger, M.: Accurately simulating anisotropic thermal conduction on a moving mesh. Mon. Not. R. Astron. Soc. 458, 410–424 (2016)
Li, R., Chen, Z., Wu, W.: Generalized Difference Methods for Differential Equations. Marcel Dekker, New York (2000)
Lipnikov, K., Manzini, G., Moulton, J.D., Shashkov, M.: The mimetic finite difference method for elliptic and parabolic problems with a staggered discretization of diffusion coefficient. J. Comput. Phys. 305, 111–126 (2016)
Lu, C., Huang, W., Van Vleck, E.S.: The cutoff method for the numerical computation of nonnegative solutions of parabolic PDEs with application to anisotropic diffusion and Lubrication-type equations. J. Comput. Phys. 242, 24–36 (2013)
Lv, J., Li, Y.: Optimal biquadratic finite volume element methods on quadrilateral meshes. SIAM J. Numer. Anal. 50, 2379–2399 (2012)
Morel, J., Roberts, R., Shashkov, M.: A local support-operators diffusion discretization scheme for quadrilateral \(r-z\) meshes. J. Comput. Phys. 144, 17–51 (1998)
Sheng, Z., Yue, J., Yuan, G.: Monotone finite volume schemes of nonequilibrium radiation diffusion equations on distorted meshes. SIAM J. Sci. Comput. 31, 2915–2934 (2009)
Shestakov, A.I., Prasad, M.K., Milovich, J.L., Gentile, N.A., Painter, J.F., Furnish, G.: The radiation-hydrodynamic ICF3D code. Comput. Methods Appl. Mech. Eng. 187, 181–200 (2000)
Sijoy, C.D., Chaturvedi, S.: TRHD: Three-temperature radiation-hydrodynamics code with an implicit non-equilibrium radiation transport using a cell-centered monotonic finite volume scheme on unstructured-grids. Comput. Phys. Commun. 190, 98–119 (2015)
Sun, W., Wu, J., Zhang, X.: A family of linearity-preserving schemes for anisotropic diffusion problems on arbitrary polyhedral grids. Comput. Methods Appl. Mech. Eng. 267, 418–433 (2013)
Wu, J., Dai, Z., Gao, Z., Yuan, G.: Linearity preserving nine-point schemes for diffusion equation on distorted quadrilateral meshes. J. Comput. Phys. 229, 3382–3401 (2010)
Wu, J., Gao, Z., Dai, Z.: A vertex-centered linearity-preserving discretization of diffusion problems on polygonal meshes. Int. J. Numer. Methods Fluids 81, 131–150 (2016)
Yang, X., Huang, W., Qiu, J.: A moving mesh finite difference method for equilibrium radiation diffusion equations. J. Comput. Phys. 298, 661–677 (2015)
Yin, L., Wu, J., Dai, Z.: A Lions domain decomposition algorithm for radiation diffusion equations on non-matching grids. Numer. Math. Theory Methods Appl. 8, 530–548 (2015)
Yin, L., Wu, J., Gao, Z.: The cell functional minimization scheme for the anisotropic diffusion problems on arbitrary polygonal grids. ESAIM: M2AN 49, 193–220 (2015)
Yin, L., Wu, J., Yao, Y.: A cell functional minimization scheme for domain decomposition method on non-orthogonal and non-matching meshes. Numer. Math. 128, 773–804 (2014)
Yin, L., Wu, J., Yao, Y.: A cell functional minimization scheme for parabolic problem. J. Comput. Phys. 229, 8935–8951 (2010)
Zel’dovich, Y.B., Raizer, Y.P.: Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena, vol. II. Academic Press, New York (1967)
Zhang, Z., Zou, Q.: Vertex-centered finite volume schemes of any order over quadrilateral meshes for elliptic boundary value problems. Numer. Math. 130, 363–393 (2015)
Zhou, Y.: Applications of Discrete Functional Analysis to the Finite Difference Methods. International Academic Publisher, Beijing (1990)
Acknowledgments
This work is partially supported by the National Natural Science Foundation of China (Nos. 11271053, 91330205, 11135007) and the Defense Industrial Technology Development Program (No. B1520133015). The author thanks the anonymous reviewers for their carefully readings and useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wu, J. Vertex-Centered Linearity-Preserving Schemes for Nonlinear Parabolic Problems on Polygonal Grids. J Sci Comput 71, 499–524 (2017). https://doi.org/10.1007/s10915-016-0309-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0309-3