Abstract
This paper is devoted to studying the boundary value method for Volterra integral equations. High order numerical schemes are devised by using special multistep collocation methods, which depend on numerical approximations of the solution in the next several steps. Stability analysis illustrates these methods enjoy wide absolutely stable regions. With the help of efficient evaluation for highly oscillatory integrals, these methods are applied to solving Volterra integral equations with highly oscillatory kernels. Both theoretical and numerical results show they share the property that the higher the oscillation, the better the accuracy of the approximations.







Similar content being viewed by others
Notes
In the remaining part, we will abbreviate \(F_n(t_{n,i})\) to [Lag Term] for simplicity.
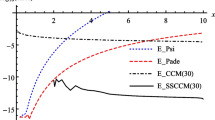
To make use of the same collocation grid as CBVM, the stepsize of CCM is chosen to be 2h.
References
Amodio, P., Mazzia, F., Trigiante, D.: Stability of some boundary value methods for the solution of initial value problems. BIT Numer. Math. 33, 434–451 (1993)
Amodio, P., Mazzia, F.: Boundary value methods based on Adams-type methods. Appl. Numer. Math. 18, 23–35 (1995)
Axelsson, A.O.H., Verwer, J.G.: Boundary value techniques for initial value problems in ordinary differential equations. Math. Comput. 45, 153–171 (1985)
Brugnano, L., Trigiante, D.: Convergence and stability of boundary value methods for ordinary differential equations. J. Comput. Appl. Math. 66, 97–109 (1996)
Brugnano, L., Trigiante, D.: Boundary value methods: the third way between linear multistep and Runge–Kutta methods. Comput. Math. Appl. 36, 269–284 (1998)
Brugnano, L., Trigiante, D.: Solving Differential Problems by Multistep Initial and Boundary Value Methods. Gordon and Breach Science Publishers, Amsterdam (1998)
Brunner, H.: Collocation Methods for Volterra Integral and Related Functional Equations. Cambridge University Press, New York (2004)
Brunner, H.: On Volterra integral operators with highly oscillatory kernels. Discret. Contin. Dyn. Syst. 34, 915–929 (2014)
Cash, J.R.: Stable Recursions. Acadamic Press, New York (1976)
Conte, D., Paternoster, B.: Multistep collocation methods for Volterra integral equations. Appl. Numer. Math. 59, 1721–1736 (2009)
Chen, H., Zhang, C.: Boundary value methods for Volterra integral and integro-differential equations. Appl. Math. Comput. 218, 2619–2630 (2011)
Chen, H., Zhang, C.: Block boundary value methods for Volterra integral and integro-differential equations. J. Comput. Appl. Math. 236, 2822–2837 (2012)
Davis, P.J.: Interpolation and Approximation. Dover Publications, New York (1975)
Fazeli, S., Hojjati, G., Shahmorad, S.: Super implicit multistep collocation methods for nonlinear Volterra integral equations. Math. Comput. Model. 55, 590–607 (2012)
Fazeli, S., Hojjati, G., Shahmorad, S.: Multistep Hermite collocation methods for solving Volterra integral equations. Numer. Algorithm 60, 27–50 (2012)
Fox, L., Mitchell, A.R.: Boundary-value techniques for the numerical solution of initial-value problems in ordinary differential equations. Q. J. Mech. Appl. Math. 10, 232–243 (1957)
Iserles, A.: On the numerical quadrature of highly oscillatory integrals I: Fourier transforms. IMA J. Numer. Anal. 24, 365–391 (2004)
Lambert, J.D.: Numerical Methods for Ordinary Differential Systems: The Initial Value Problem. Wiley, Chichester (1991)
Lopez, L., Trigiante, D.: Boundary value methods and BV-stability in the solution of initial value problems. Appl. Numer. Math. 11, 225–239 (1993)
Ma, J., Xiang, S., Kang, H.: On the convergence rates of Filon methods for the solution of a Volterra integral equation with a highly oscillatory Bessel kernel. Appl. Math. Lett. 26, 699–705 (2013)
Ma, J., Fang, C., Xiang, S.: Modified asymptotic orders of the direct Filon method for a class of Volterra integral equations. J. Comput. Appl. Math. 281, 120–125 (2015)
Marzulli, P., Trigiante, D.: Stability and convergence of boundary value methods for solving ODE. J. Differ. Equ. Appl. 1, 45–55 (1995)
Miller, J.C.P.: Bessel Functions, Part II, Mathematical Table X. Cambridge University Press, Cambridge (1952)
Olver, F.W.J.: Numerical solution of second-order linear difference equations. J. Res. Natl. Bur. Stand. 71B, 111–129 (1967)
Olver, F.W.J., Sooke, D.J.: Note on backward recurrence algorithms. Math. Comput. 26, 941–947 (1972)
Trefethen, L.N.: Is Gauss quadrature better than Clenshaw–Curtis? SIAM Rev. 50, 67–87 (2008)
Xiang, S.: Efficient Filon-type methods for \(\int _a^b f(x)e^{i\omega g(x)}dx\). Numer. Math. 105, 633–658 (2007)
Xiang, S., Wu, Q.: Numerical solutions to Volterra integral equations of the second kind with oscillatory trigonometric kernels. Appl. Math. Comput. 223, 34–44 (2013)
Xiang, S.: Laplace transforms for approximation of highly oscillatory Volterra integral equations of the first kind. Appl. Math. Comput. 232, 944–954 (2014)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Additional information
This work is supported by No.11371376 of NSF of China, the Innovation-Driven Project and the Mathematics and Interdisciplinary Sciences Project of Central South University.
Rights and permissions
About this article
Cite this article
Ma, J., Xiang, S. A Collocation Boundary Value Method for Linear Volterra Integral Equations. J Sci Comput 71, 1–20 (2017). https://doi.org/10.1007/s10915-016-0289-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0289-3