Abstract
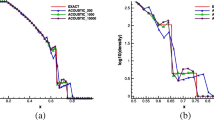
We propose, analyze, and test a new MHD discretization which decouples the system into two Oseen problems at each timestep yet maintains unconditional stability with respect to the time step size, is optimally accurate in space, and behaves like second order in time in practice. The proposed method chooses a parameter \(\theta \in [0,1]\), dependent on the viscosity \(\nu \) and magnetic diffusivity \(\nu _m\), so that the explicit treatment of certain viscous terms does not cause instabilities, and gives temporal accuracy \(O(\Delta t^2 + (1-\theta )|\nu -\nu _m|\Delta t)\). In practice, \(\nu \) and \(\nu _m\) are small, and so the method behaves like second order. When \(\theta =1\), the method reduces to a linearized BDF2 method, but it has been proven by Li and Trenchea that such a method is stable only in the uncommon case of \(\frac{1}{2}< \frac{\nu }{\nu _m} < 2\). For the proposed method, stability and convergence are rigorously proven for appropriately chosen \(\theta \), and several numerical tests are provided that confirm the theory and show the method provides excellent accuracy in cases where usual BDF2 is unstable.




Similar content being viewed by others
References
Akbas, M., Rebholz, L., Tone, F.: A note on the importance of mass conservation in long-time stability of Navier–Stokes equations. Appl. Math. Lett. 45, 98–102 (2015)
Arnold, D., Qin, J.: Quadratic velocity/linear pressure Stokes elements. In: Vichnevetsky, R., Knight, D., Richter, G. (eds.) Advances in Computer Methods for Partial Differential Equations, VII edn, pp. 28–34. IMACS, NewYork (1992)
Barleon, L., Casal, V., Lenhart, L.: MHD flow in liquid-metal-cooled blankets. Fusion Eng. Des. 14, 401–412 (1991)
Barrow, J.D., Maartens, R., Tsagas, C.G.: Cosmology with inhomogeneous magnetic fields. Phys. Rep. 449, 131–171 (2007)
Benzi, M., Olshanksii, M.A.: An augmented Lagrangian-based approach to the Oseen problem. SIAM J. Sci. Comput. 28(6), 2095–2113 (2005)
Biskamp, D.: Magnetohydrodynamic Turbulence. Cambridge University Press, Cambridge (2003)
Bodenheimer, P., Laughlin, G.P., Rozyczka, M., Yorke, H.W.: Numerical Methods in Astrophysics. Taylor & Francis, New York (2007). Series in Astronomy and Astrophysics
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, vol. 15. Springer, New York (1994). Texts in Applied Mathematics
Cho, J., Vishniac, E.T.: The anisotropy of magnetohydrodynamic Alfvénic turbulence. Astrophys. J. 539, 273–282 (2000)
Davidson, P.A.: An Introduction to Magnetohydrodynamics. Cambridge University Press, Cambridge (2001)
Dormy, E., Soward, A.M.: Mathematical aspects of natural dynamos. Grenoble Sciences. Universite Joseph Fourier, Grenoble, VI, Fluid Mechanics of Astrophysics and Geophysics (2007)
Elman, H.C., Silvester, D.J., Wathen, A.J.: Performance and analysis of saddle point preconditioners for the discrete steady-state Navier–Stokes equations. Numer. Math. 90, 665–688 (2002)
Elsässer, W.M.: The hydromagnetic equations. Phys. Rev. 79, 183 (1950)
Font, J.A.: Gerneral Relativistic Hydrodynamics and Magnetohydrodynamics: Hyperbolic System in Relativistic Astrophysics, in Hyperbolic Problems: Theory, Numerics, Applications. Springer, Berlin (2008)
Girault, V., Raviart, P.A.: Finite Element Approximation of the Navier–Stokes Equations. Lecture Notes in Mathematics, 749th edn. Springer, Berlin (1979)
Gunzburger, M.: Iterative penalty methods for the Stokes and Navier–Stokes equations. In: Proceedings from Finite Element Analysis in Fluids conference, University of Alabama, Huntsville, pp. 1040–1045 (1989)
Gunzburger, M.D.: Finite Element Methods for Viscous Incompressible Flows: A Guide to Theory, Practice, and Algorithms. Academic Press, Boston (1989)
Hashizume, H.: Numerical and experimental research to solve MHD problem in liquid blanket system. Fusion Eng. Des. 81, 1431–1438 (2006)
Hecht, F.: New development in Freefem++. J. Numer. Math. 20, 251–266 (2012)
Heywood, J.G., Rannacher, R.: Finite-element approximation of the nonstationary Navier–Stokes problem part IV: error analysis for second-order time discretization. SIAM J. Numer. Anal. 27, 353–384 (1990)
Hillebrandt, W., Kupka, F.: Interdisciplinary Aspects of Turbulence. Lecture Notes in Physics, 756th edn. Springer, Berlin (2009)
Jones, C.A.: Thermal and compositional convection in the outer core. Treatise Geophys. 8, 131–185 (2007)
Konshin, I.N., Olshanskii, M.A., Vassilevski, YuV: ILU preconditioners for non-symmetric saddle point matrices with application to the incompressible Navier–Stokes equations. SIAM J. Sci. Comp. 37, 2171–2197 (2015)
Landau, L.D., Lifshitz, E.M.: Electrodynamics of Continuous Media. Pergamon Press, Oxford (1960)
Li, Y., Trenchea, C.: Partitioned second order method for magnetohydrodynamics in Elsasser fields. Submitted (2015)
Akbas, M., Kaya, S., Mohebujjaman, M., Rebholz, L.: Numerical analysis and testing of a fully discrete, decoupled penalty-projection algorithm for MHD in Elsässer variable. Int. J. Numer. Anal. Model. 13(1), 90–113 (2016)
Olson, P.: Experimental dynamos and the dynamics of planetary cores. Ann. Rev. Earth Planet. Sci. 41, 153–181 (2013)
Punsly, B.: Black Hole Gravitohydrodynamics. Astrophysics and Space Science Library, vol. 355, 2nd edn. Springer, Berlin (2008)
Qin, J., Zhang, S.: Stability and approximability of the P1–P0 element for Stokes equation. Int. J. Numer. Methods Fluids 54(5), 497–515 (2007)
Rebholz, L., Xiao, M.: On reducing the splitting error in Yosida methods for the Navier–Stokes equations with grad-div stabilization. Comput. Methods Appl. Mech. Eng. 294, 259–277 (2015)
Smolentsev, S., Moreau, R., Buhler, L., Mistrangelo, C.: MHD thermofluid issues of liquid-metal blankets: phenomena and advances. Fusion Eng. Des. 85, 1196–1205 (2010)
Trenchea, C.: Unconditional stability of a partitioned IMEX method for magnetohydrodynamic flows. Appl. Math. Lett. 27, 97–100 (2014)
Wacker, B., Arndt, D., Lube, G.: Nodal-based finite element methods with local projection stabilization for linearized incompressible magnetohydrodynamics. Submitted (2015)
Zhang, S.: A new family of stable mixed finite elements for the 3d Stokes equations. Math. Comput. 74, 543–554 (2005)
Zhang, S.: Quadratic divergence-free finite elements on Powell–Sabin tetrahedral grids. Calcolo 48(3), 211–244 (2011)
Acknowledgments
All authors were partially supported by NSF grant DMS1522191. T. Heister was partially supported by the Computational Infrastructure in Geodynamics initiative (CIG), through the National Science Foundation under Award No. EAR-0949446 and The University of California–Davis. Clemson University is acknowledged for generous allotment of compute time on the Palmetto cluster.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
We prove here a conditional stability result for the full second order method, i.e. when \(\theta =1\), which does not assume \(\frac{1}{2}<Pr_m<2\). The condition is that \(\Delta t \le \frac{h^2(\nu +\nu _m-|\nu -\nu _m|)}{C_i(\nu -\nu _m)^2}\), where \(C_i\) an the inverse inequality constant, and thus if \(\nu -\nu _m\) is not small (which is equivalent to \(Pr_m\) near 1), this can be a severe timestep restriction when fine meshes are used.
Lemma 6.1
Consider Algorithm 3.1 with \(\theta =1\) (the full second order method). If the mesh is sufficiently regular so that the inverse inequality holds (with constant \(C_i\)) and the time step is chosen to satisfy
then the method is stable and solutions satisfy
Proof
Choose \(\theta =1,\chi _h=v_h^{n+1}\in V_h\) and \(l_h=w_h^{n+1}\in V_h\) in Algorithm 3.1, (3.1)–(3.2). This vanishes the nonlinear and pressure terms, and leaves
Using the usual BDF2 identity on the time derivative terms and adding the equations yields
and then adding and subtracting the term \(\frac{\nu -\nu _m}{2}\left( \nabla v_h^{n+1},\nabla w_h^{n+1}\right) \) provides
Using Cauchy–Schwarz and Young’s inequalities we have that
Young’s inequality provides the following bounds on the last five terms in (6.5):
Combining, we now have that
The inverse inequality provides the estimate
which allows Eq. (6.6) to be written as
Now using the assumption on the time step size and applying standard techniques completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Heister, T., Mohebujjaman, M. & Rebholz, L.G. Decoupled, Unconditionally Stable, Higher Order Discretizations for MHD Flow Simulation. J Sci Comput 71, 21–43 (2017). https://doi.org/10.1007/s10915-016-0288-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0288-4