A method for convex black-box integer global optimization

Abstract

We study the problem of minimizing a convex function on a nonempty, finite subset of the integer lattice when the function cannot be evaluated at noninteger points. We propose a new underestimator that does not require access to (sub)gradients of the objective; such information is unavailable when the objective is a blackbox function. Rather, our underestimator uses secant linear functions that interpolate the objective function at previously evaluated points. These linear mappings are shown to underestimate the objective in disconnected portions of the domain. Therefore, the union of these conditional cuts provides a nonconvex underestimator of the objective. We propose an algorithm that alternates between updating the underestimator and evaluating the objective function. We prove that the algorithm converges to a global minimum of the objective function on the feasible set. We present two approaches for representing the underestimator and compare their computational effectiveness. We also compare implementations of our algorithm with existing methods for minimizing functions on a subset of the integer lattice. We discuss the difficulty of this problem class and provide insights into why a computational proof of optimality is challenging even for moderate problem sizes.

Appendices

A Proofs of Lemmas

1.1 A.1 Proof of Lemma 4

Proof

For contradiction, suppose that the set $\{x^0\} \cup X \setminus \{x^{n+1}\}$ is not poised and therefore is affinely dependent. Then, there must exist scalars $\beta _j$ not all zero, and (without loss of generality) $x^n \in X$ such that

$$\begin{aligned} \sum _{j=0}^{n-1} \beta _j (x^j - x^n) = 0. \end{aligned}$$

(21)

Replacing $x^0$ with (9) in the left-hand side above yields

$$\begin{aligned} 0&= \beta _0\left( \sum _{j=1,j\ne n}^{n+1} \alpha _j x^j + (\alpha _n -1)x^n\right) + \sum _{j=1}^{n-1} \beta _j (x^j - x^n) \nonumber \\&= \sum _{j = 1}^{n-1} (\beta _0 \alpha _j + \beta _j) x^j + \bigg (\beta _0(\alpha _n -1) -\sum _{j = 1}^{n-1} \beta _j \bigg ) x^n + \beta _0 \alpha _{n+1}x^{n+1}. \end{aligned}$$

(22)

Since X is poised, the vectors $\{ x^1,\ldots , x^{n+1}\}$ are affinely independent; by definition of affine independence, the only solution to $\sum _{j=1}^{n+1} \gamma _j x^j = 0$ and $\sum _{j=1}^{n+1} \gamma _j = 0$ is $\gamma _j = 0$ for $j = 1,\ldots ,n+1$. The sum of the coefficients from (22) satisfies

$$\begin{aligned} \sum _{j = 1}^{n-1} (\beta _0 \alpha _j + \beta _j) + \beta _0(\alpha _n - 1) -\sum _{j=1}^{n-1}\beta _j + \beta _0 \alpha _{n+1} = \beta _0 \sum _{j = 1}^{n+1} \alpha _j - \beta _0 = 0, \end{aligned}$$

because $\sum _{j=1}^{n+1}\alpha _j = 1$. This means that all coefficients of $x^j$ in (22) are also equal to zero. Since $\alpha _{n+1}>0$, the last term from (22) implies that $\beta _0 = 0$. Considering the remaining coefficients in (22), we conclude that $\beta _0 \alpha _j + \beta _j=0$, which implies that $\beta _j = 0$ for $j=1,\ldots , n-1$. This contradicts the assumption that not all $\beta _j = 0$. Hence, the result is proved. $\square$

1.2 A.2 Proof of Lemma 5

Proof

Since $x^0 \in \mathrm {int}\left( \mathrm {conv}\left( X\right) \right)$, there exist $\alpha _j > 0$ such that

$$\begin{aligned} 0 = \left( \sum _{j = 1}^{n+1} \alpha _j\right) (x^0 - x^0) = \left( \sum _{j = 1}^{n+1} \alpha _j\right) x^0 - \sum _{j = 1}^{n+1} \alpha _j x^j = \sum _{j = 1}^{n+1} \alpha _j (x^0-x^j), \end{aligned}$$

(23)

where the second equality follows from (9). The existence of $\alpha _j>0$ such that $\sum _{j=1}^{n+1}\alpha _j (x^0-x^j) = 0$ implies that the vectors $\left\{ x^0-x^j: j \in \{ 1,\ldots ,n+1\}\right\}$ are a positive spanning set (see, e.g., [15, Theorem 2.3 (iii)]). Therefore any $x \in {\mathbb {R}}^n$ can be expressed as

$$\begin{aligned} x = \sum _{j=1}^{n} \alpha _j (x^0-x^j), \end{aligned}$$

with $\alpha _j \ge 0$ for all j.

We will show that any $x \in {\mathbb {R}}^n$ belongs to ${\mathcal {U}}^{{{\varvec{i}}}}$ for some multi-index ${{\varvec{i}}}$ containing $x^0$. By Lemma 4, every set of n distinct vectors of the form $(x^0 - x^j)$ for $x^j \in X$ is a linearly independent set. Thus we can express

$$\begin{aligned} x - x^0 = \sum _{j=1,j \ne l}^{n+1} \lambda _j (x^0 - x^j), \end{aligned}$$

(24)

for some $l \in \{1, \ldots n+1 \}$. If $\lambda _j \ge 0$ for each j, then we are done, and $x \in \mathrm {cone}\big (x^0 - X \setminus \{x^l\}\big )$.

Otherwise, choose an index $j'$ such that $\lambda _{j'}$ is the most negative coefficient on the right of (24) (breaking ties arbitrarily). Using (23), we can exchange the indices l and $j'$ in (24) by observing that

$$\begin{aligned} \lambda _{j'} (x^0 - x^{j'}) = \frac{-\lambda _{j'}}{\alpha _{j'}}\left( \sum _{j = 1,j \ne j'}^{n+1} \alpha _j (x^0-x^j)\right) . \end{aligned}$$

Note that $\frac{-\lambda _{j'}}{\alpha _{j'}}\alpha _j>0$ by (9), and we can rewrite (24) as

$$\begin{aligned} x - x^0 = \sum _{j=1,j \ne j'}^{n+1} \mu _j (x^0 - x^j), \end{aligned}$$

(25)

with new coefficients $\mu _j$ that are strictly larger than $\lambda _j$:

$$\begin{aligned} \mu _j = \left\{ \begin{array}{ll} \displaystyle \lambda _j - \frac{\lambda _{j'}}{\alpha _{j'}}\alpha _j > \lambda _j, \quad &{} j \not = l, j \not = j' \\ - \frac{\lambda _{j'}}{\alpha _{j'}}\alpha _j \quad &{} j = l . \end{array} \right. \end{aligned}$$

Observe that (25) has the same form as (24) but with coefficients $\mu _j$ that are strictly greater than $\lambda _j$. We can now define $\lambda =\mu$ and repeat the process. If there is some $\lambda _{j'}<0$, the process will strictly increase all $\lambda _j$. Because there are only a finite number of subsets of size n, we must eventually have all $\lambda _j \ge 0$. Once $\lambda _{j'}$ has been pivoted out, it can reenter only with a positive value (like $\mu _l$ above), so eventually all $\lambda _j$ will be nonnegative. $\square$

1.3 A.3 Proof of Lemma 6

Proof

Let ${{\varvec{i}}}$ be given and $i_j \in {{\varvec{i}}}$ fixed. We first show that $\mathrm {cone}\big (x^{i_j} - X^{{{\varvec{i}}}}\big ) \subseteq F^{i_j}$ by showing that an arbitrary $x \in \mathrm {cone}\big (x^{i_j} - X^{{{\varvec{i}}}}\big )$ satisfies (20) for each $i_l \in {{\varvec{i}}}, i_l \ne i_j$. Given $(c^{i_l},b^{i_l})$ satisfying (18) and (19), then using the definition (5) yields

$$\begin{aligned} (c^{i_l})^{{\text {T}}}x + b^{i_l}&= (c^{i_l})^{{\text {T}}}\left( x^{i_j} + \sum _{k=1, k\ne j}^{n+1} \lambda _k (x^{i_j} - x^{i_k})\right) + b^{i_l}\\&= (c^{i_l})^{{\text {T}}}x^{i_j} + b^{i_l} + \sum _{k=1, k\ne j}^{n+1} \lambda _k (c^{i_l})^{{\text {T}}}x^{i_j} - \sum _{k=1, k\ne j}^{n+1} \lambda _k (c^{i_l})^{{\text {T}}}x^{i_k} \\&= 0 + \sum _{k=1, k\ne j}^{n+1} \lambda _k \left( (c^{i_l})^{{\text {T}}}x^{i_j} + b^{i_l} \right) - \sum _{k=1, k\ne j}^{n+1} \lambda _k \left( (c^{i_l})^{{\text {T}}}x^{i_k} + b^{i_l} \right) \\&= 0 - \sum _{k=1, k\ne j}^{l-1} \lambda _k \left( (c^{i_l})^{{\text {T}}}x^{i_k} + b^{i_l} \right) - \lambda _l \left( (c^{i_l})^{{\text {T}}}x^{i_l} + b^{i_l} \right) \\&\quad - \sum _{k=l+1, k\ne j}^{n+1} \lambda _k \left( (c^{i_l})^{{\text {T}}}x^{i_k} + b^{i_l} \right) \\&= - \lambda _l \left( (c^{i_l})^{{\text {T}}}x^{i_l} + b^{i_l} \right) \le 0, \end{aligned}$$

where we have used (18) in the last three equations. The final inequality holds because $\lambda _l \ge 0$ by (5) and $(c^{i_l})^{{\text {T}}}x^{i_l} + b^{i_l} > 0$ by (19). Because $i_l$ is arbitrary, it follows that any x in $\mathrm {cone}\big (x^{i_j} - X\big )$ is also in $F^{i_j}$.

We now show that $F^{i_j} \subseteq \mathrm {cone}\big (x^{j} - X^{{{\varvec{i}}}}\big )$ by contradiction. If $x \notin \mathrm {cone}\big (x^{i_j} - X^{{{\varvec{i}}}}\big )$ for a set of $n+1$ poised points $X^{{{\varvec{i}}}}$, then x can be represented as $x^{i_j} +\displaystyle \sum \nolimits _{l=1, l\ne j}^{n+1} \lambda _l \left( x^{i_j} - x^{i_l} \right)$ only with some $\lambda _{l} < 0$. Thus, (20) is violated for some l, and hence $x \notin F^{i_j}$. $\square$

B Test problems

Table 3 Set of convex test problems and their minimizers on the domain $\left[ -K,K \right] ^{n} \cap {\mathbb {Z}}^n$

C Performance of MILP model

Table 4 Characteristics of the first 12 instances of (CPF) generated by Algorithm 1 minimizing the convex quadratic function abhi on $\varOmega =[-2,2]^3 \cap {\mathbb {Z}}^3$. (CPF) instances are generated by AMPL and solved by CPLEX; times are the mean of five replications

Fig. 10

Characteristics of the first 12 instances of (CPF) generated by Algorithm 1 minimizing the convex quadratic abhi on $\varOmega =[-2,2]^3 \cap {\mathbb {Z}}^3$. Left shows the lower bound and solution time (mean of five replications and maximum and minimum times are also shown); right shows the number of binary and continuous variables and constraints. For further details of these 12 MILP models, see Table 4

Table 4 shows the size of the MILP model at each iteration and the computational effort required for solving it. The column k refers to the iteration of Algorithm 1, sHyp denotes the number of secants (i.e., $\left| W(X) \right|$), and LB and UB give the lower and upper bound on f on $\varOmega$, respectively. We show the computational effort needed to solve each MILP via time, the mean solution time (in seconds) for 5 replications; simIter, the number of simplex iterations; and nodes, the number of branch-and-bound nodes explored by the MILP solver. The size of each MILP (after presolve) is shown in terms of bVars, the number of binary variables; cVars, the number of continuous variables; and cons, the number of constraints. Table 4 also shows the optimal solution ${\hat{x}}$ of each MILP. These experiments were performed by using CPLEX (v.12.6.1.0) on a 2.20 GHz, 12-core Intel Xeon computer with 64 GB of RAM. For this small problem we see that the size of the MILP grows exponentially as the iterations proceed, which results in an exponential growth in solution time as illustrated in Fig. 10. The iteration 13 MILP was not solved after 30 minutes.

D Detailed numerical results

Tables 5, 6 contain detailed numerical results for the interested reader. Note that some solvers do not respect the given budget of function evaluations. We have used a different stopping criterion for MATSuMoTo: it is set to stop only when a point with the optimal value has been identified. Also, although the global minimum is the starting point for entropy, infnorm, onenorm, maxq and mxhilb, MATSuMoTo instead uses its initial symmetric Latin hypercube design. The last row of Table 1 in Sect. 2 shows $\left| \varOmega \right|$ for these problems (Fig. 11).

Table 5 Number of function evaluations taken by solvers for 8 of the 16 base problems and various values of n and K. For MATSuMoTo, the nearest value less than the median of the number of the evaluations of 20 replications is chosen

Table 6 Number of function evaluations taken by solvers for 8 of the 16 base problems and various values of n and K. For MATSuMoTo, the nearest value less than the median of the number of the evaluations of 20 replications is chosen

E Derivation of tolerances

In this section, we show how one can compute sufficient values of $M_{\eta }$, $\epsilon _{\lambda }$, and $M_{\lambda }$ for the MILP model (CPF). We first show that if we choose these parameters incorrectly, then the resulting MILP model no longer provides a valid lower bound.

Effect of an Insufficient $\epsilon _\lambda$ Value. A large $\epsilon _\lambda$ or small $M_\lambda$ (or both) could result in an incorrect value of $z^{i_j}=1$ for a point $x \notin \mathrm {cone}\big (x^{i_j}-X^{{{\varvec{i}}}}\big )$, violating the implication of $z^{i_j}=1$ and yielding an invalid lower bound on f. This is illustrated using a one-dimensional example in Fig. 12. Similarly, one can encounter an invalid lower bound at an iteration if $M_\lambda$ is chosen to be smaller than required.

Fig. 11

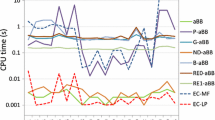
Number of evaluations for 8 test functions on $\left[ -4,4 \right] ^5 \cap {\mathbb {Z}}^n$ before SUCIL first identifies a global minimum and evaluations required to prove its global optimality. The fewest number of evaluations required by any of DFLINT, DFLINT-M, NOMAD, NOMAD-dm, and MATSuMoTo is shown for comparison

Fig. 12

An example of false termination of Algorithm 1 using (CPF) when an insufficient value of $\epsilon _\lambda$ is used: $f(x)=x^2$ and interpolation points $-1$ and 1 are used to form the secant shown in red colour. Any value of $\epsilon _\lambda > 0.5$ forces $z^{{1}_1}=z^{{1}_2}=1$, activating the cut $\eta \ge 1$ at the optimal $x^*=0$, resulting in $l_f^k=u_f^k=1$

Bound on $M_{\eta }$ Let $l_f$ be a valid lower bound of f on $\varOmega$. With this lower bound, scalars $M_{{{\varvec{i}}}}$ can be defined as

$$\begin{aligned} M_{{{\varvec{i}}}}=\max \limits _{x \in \varOmega }\{(c^{{{\varvec{i}}}})^T x + b^{{{\varvec{i}}}}\} - l_f, \; \forall {{\varvec{i}}}\in W(X). \end{aligned}$$

(26)

If $\varOmega = \left\{ x: l_x \le x \le u_x \right\}$, where $l_x, u_x \in {\mathbb {R}}^n$ are known, then we can set

$$\begin{aligned} M_{{{\varvec{i}}}} = \sum _{h:c^{{{\varvec{i}}}}_j<0}c^{{{\varvec{i}}}}_h l_x + \sum _{h:c^{{{\varvec{i}}}}_j \ge 0}c^{{{\varvec{i}}}}_h u_x + b^{{{\varvec{i}}}} - l_f, \quad h = 1, \ldots , n, \; \forall {{\varvec{i}}}\in W(X). \end{aligned}$$

(27)

Then, we can either set individual values of $M_{{{\varvec{i}}}}$ within each constraint (10), which would yield a tighter model, or use a single parameter,

$$\begin{aligned} M_{\eta }=\max \limits _{{{\varvec{i}}}} \{M_{{{\varvec{i}}}}\}, \end{aligned}$$

(28)

as shown in (CPF).

Bounds on $\epsilon _\lambda$ and $M_\lambda$ Sufficient values of $M_\lambda$ and $\epsilon _\lambda$ are not easy to calculate as they depend on the rays generated at $x^{i_j}$, and the domain $\varOmega$. We show next, that bounds on these values can be computed by solving a set of optimization problems. A sufficient value for $\epsilon _\lambda$ can be computed based on the representations of the $n+1$ hyperplanes formed using different combinations of n points, $\forall {{\varvec{i}}}\in W(X)$. We can use one of the representations of the hyperplane passing through points $X^{i}\setminus \{x^{i_j}\}, j=1\ldots n+1$ to obtain bounds on $\epsilon _\lambda$, by solving an optimization problem for each $i_j \in {{\varvec{i}}}$. Let $c^{{{\varvec{i}}}_{i_j-}}$ and $b^{{{\varvec{i}}}_{i_j-}}$ denote the solution of the following problem.

Problem (P$-hyp$) can be easily cast as an integer program by replacing $\left\| c \right\| _1$ by $e^Ty$, where $e=(1,\ldots ,1)^T$ is the vector or all ones, and the variables y satisfy the constraints $y \ge c, y \ge - c$. Because, the hyperplane is generated using n integer points, it can be shown that there exists a solution $c^{{{\varvec{i}}}_{i_j-}}$ and $b^{{{\varvec{i}}}_{i_j-}}$ that is nonzero and integral, as stated in the following proposition.

Proposition 1

Consider a hyperplane $S=\{x:c^{T} x + b = 0\}$ such that c and b are integral. The Euclidean distance between an arbitrary point ${\hat{x}} \in {\mathbb {Z}}^n \setminus S$, and S, is greater than or equal to $\frac{1}{||c ||_2}$.

Proof

The Euclidean distance between a point ${\hat{x}}$ and S is the 2-norm of the projection of the line segment joining an arbitrary point $w \in S$ and ${\hat{x}}$, on the normal passing through ${\hat{x}}$, and can be expressed as

$$\begin{aligned} \frac{|c^{T} {\hat{x}} + b |}{||c ||_2} . \end{aligned}$$

(29)

By integrality of c, b and ${\hat{x}}$, and since ${\hat{x}} \notin S$, $|c^{T} {\hat{x}} + b |\ge 1$, and the result follows. $\square$

Proposition 1 can be used directly to get a sufficient value of $\epsilon _\lambda$ as follows.

$$\begin{aligned} \epsilon _\lambda = \min \limits _{{{\varvec{i}}}\in W(X),\; i_j \in {{\varvec{i}}}}{\; \frac{1}{||c^{{{\varvec{i}}}_{i_j-}} ||_2}} . \end{aligned}$$

(30)

The bound can be tightened using the following optimization problem.

If we denote by $\epsilon ^{{{\varvec{i}}}_{i_j-}}_\lambda$, the optimal value of (P-$\epsilon$), then the following is a sufficient value of $\epsilon _\lambda$.

$$\begin{aligned} \epsilon _\lambda = \min \limits _{{{\varvec{i}}}\in W(X),\; i_j \in {{\varvec{i}}}}{\; \epsilon _\lambda ^{{{\varvec{i}}}_{i_j-}}}. \end{aligned}$$

(31)

Similarly, if we maximize the objective in (P-$\epsilon$), and denote the optimal value by $M^{{{\varvec{i}}}_{i_j-}}_\lambda$ we get a sufficient value for $M_\lambda$ as follows.

$$\begin{aligned} M_\lambda = \max \limits _{{{\varvec{i}}}\in W(X),\; i_j \in {{\varvec{i}}}}{\; M_\lambda ^{{{\varvec{i}}}_{i_j-}}}. \end{aligned}$$

(32)

No-Good Cuts and Stronger Objective Bounds. For our initial experiments, we tried setting arbitrarily small values for $\epsilon _{\lambda }$ instead of obtaining the best possible values by solving a set of optimization problems as elaborated above. The problem with having such values of $\epsilon _{\lambda }>0$ too small is that it allows us to ignore the cuts at the interpolation points, $x^{(k)}$, causing a violation of the bound, $\eta \ge f^{(k)}$, for $x=x^{(k)}$ in the MILP, resulting in repetition of iterates in the algorithm. We fixed this by adding the following valid inequality to the MILP.

$$\begin{aligned} \eta \ge f^{(k)} - M \Vert x^{(k)} - x \Vert _1 . \end{aligned}$$

We can write this inequality as a linear constraint, by introducing a binary representation of the variables, x, requiring nU binary variables, $\xi _{ij}, \; i=1,\ldots ,n, \; j=1,\ldots ,U$, where n is the dimension of our problem, and $0 \le x \le U$. With this representation, we obtain

$$\begin{aligned} x_i = \sum _{j=1}^U i \xi _{ij}, \quad 1= \sum _{j=1}^U \xi _{ij}, \quad \xi _{ij} \in \{0,1\}, \end{aligned}$$

and write the $\eta$-constraint equivalently as

$$\begin{aligned} \eta \ge f^{(k)} - M \sum _{i=1}^n \left( \sum _{j: \xi _{ij}^{(k)}=0} \xi _{ij} + \sum _{j: \xi _{ij}^{(k)}=1} \left( 1 - \xi _{ij} \right) \right) . \end{aligned}$$