Eco-friendly container transshipment route scheduling problem with repacking operations | Journal of Combinatorial Optimization Skip to main content
Springer Nature Link
Log in

Eco-friendly container transshipment route scheduling problem with repacking operations

  • Published:
Journal of Combinatorial Optimization Aims and scope Submit manuscript

Abstract

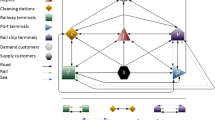
Currently, a huge amount of cargo is transported via containers by liner shipping companies. Under stochastic demand, repacking operations and carbon reduction, which may lead to an increase in effectiveness and environmental improvement, have been rarely considered in previous literature. In this paper, we investigate a container transshipment route scheduling problem with repacking operations under stochastic demand and environmental protection. The problem is a combinatorial optimization problem. Lacking historical data, a chance-constrained programming model is proposed to minimize the total operating and environment-related costs. We choose two distribution-free approaches, i.e., approximation based in Markov’s Inequality and Mixed Integer Second-Order Conic Program to approximate the chance constraints. As the loses induced by unfulfilled demand are not taken into account in the above model, a scenario-based model is developed considering the loses. Risk-neutral model may provide solutions that perform poorly while considering uncertainty. To incorporate decision makers’ perspectives, therefore, we also propose a risk-averse model adopting a risk aversion measure called Conditional Value-at-Risk to meet different preferences. Finally, we conduct computational experiments based on real data to compare the performances of the modeling methods and illustrate the impacts by testing different risk levels and confidence levels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Artzner P, Delbaen F, Eber J, Heath D (1999) Coherent measures of risk. Math Finance 9:203–228

    MathSciNet  MATH  Google Scholar 

  • Artzner P, Delbaen F, Eber J, Heath D (1997) Thinking coherently. Risk 10:68–71

    Google Scholar 

  • Balakrishnan A, Karsten C (2017) Container shipping service selection and cargo routing with transshipment limits. Eur J Oper Res 263(2):652–663

    MathSciNet  MATH  Google Scholar 

  • Bentaha M, Battaïa O, Dolgui A, Hu S (2015) Second order conic approximation for disassembly line design with joint probabilistic constraints. Eur J Oper Res 247(3):957–967

    MathSciNet  MATH  Google Scholar 

  • Chao S, Yu M, Hsieh W (2018) Evaluating the efficiency of major container shipping companies: a framework of dynamic network DEA with shared inputs. Transp Res Part A 117:44–57

    Google Scholar 

  • Charnes A, Cooper W, Symonds G (1958) Cost horizons and certainty equivalents: an approach to stochastic programming of heating oil. Manag Sci 4(3):235–263

    Google Scholar 

  • Chen J, Jia S, Wang S, Liu Z (2018) Subloop-based reversal of port rotation directions for container liner shipping network alteration. Transp Res Part B 118:336–361

    Google Scholar 

  • Chen W, Sim M, Sun J, Teo C (2010) From CVaR to uncertainty set: implications in joint chance-constrained optimization. Oper Res 58(2):470–485

    MathSciNet  MATH  Google Scholar 

  • Delage E, Ye Y (2010) Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper Res 58(3):595–612

    MathSciNet  MATH  Google Scholar 

  • Ding X, Hua D, Jiang G, Bao Z, Yu L (2017) Two-stage interval stochastic chance-constrained robust programming and its application in flood management. J Clean Prod 167:908–918

    Google Scholar 

  • Elçi Ö, Noyan N, Bülbül K (2018) Chance-constrained stochastic programming under variable reliability levels with an application to humanitarian relief network design. Comput Oper Res 96:91–107

    MathSciNet  MATH  Google Scholar 

  • Escudero L, Monge J, Romero Morales D (2015) An SDP approach for multiperiod mixed 0C1 linear programming models with stochastic dominance constraints for risk management. Comput Oper Res 58:32–40

    MathSciNet  MATH  Google Scholar 

  • Fitzgerald W, Howitt O, Smith I, Hume A (2011) Energy use of integral refrigerated containers in maritime transportation. Energy Policy 39(4):1885–1896

    Google Scholar 

  • Gao Y, Qin Z (2016) A chance constrained programming approach for uncertain \(p\)-hub center location problem. Comput Ind Eng 102:10–20

    Google Scholar 

  • Hu J, Huang Y, Zhao X (2019) Research on the slot allocation of container liner under E-commerce environment. Comput Ind Eng 129:556–562

    Google Scholar 

  • Jeong Y, Saha S, Chatterjee D, Moon I (2018) Direct shipping service routes with an empty container management strategy. Transp Res Part E 118:123–142

    Google Scholar 

  • Kallio M, Hardoroudi N (2018) Second-order stochastic dominance constrained portfolio optimization: theory and computational tests. Eur J Oper Res 264(2):675–685

    MathSciNet  MATH  Google Scholar 

  • Kınay Ö, Kara B, Saldanha-da-Gama F, Correia I (2018) Modeling the shelter site location problem using chance constraints: a case study for Istanbul. Eur J Oper Res 270(1):132–145

    MathSciNet  MATH  Google Scholar 

  • Koza D (2019) Liner shipping service scheduling and cargo allocation. Eur J Oper Res 275(3):897–915

    MathSciNet  MATH  Google Scholar 

  • Liu K, Li Q, Zhang Z (2019) Distributionally robust optimization of an emergency medical service station location and sizing problem with joint chance constraints. Transp Res Part B 119:79–101

    Google Scholar 

  • Nemirovski A, Shapiro A (2006) Convex approximations of chance constrained programs. Soc Ind Appl Math 17(4):969–996

    MathSciNet  MATH  Google Scholar 

  • Ng MW (2015) Container vessel fleet deployment for liner shipping with stochastic dependencies in shipping demand. Transp Res Part B 74:79–87

    Google Scholar 

  • Ng MW (2014) Distribution-free vessel deployment for liner shipping. Eur J Oper Res 238(3):858–862

    MathSciNet  MATH  Google Scholar 

  • Noyan N (2018) Risk-Averse Stochastic Modeling and Optimization, Chapter 10: 221-254, Available: https://pubsonline.informs.org/doi/abs/10.1287/educ.2018.0183

  • Noyan N (2012) Risk-averse two-stage stochastic programming with an application to disaster management. Comput Oper Res 39(3):541–559

    MathSciNet  MATH  Google Scholar 

  • Noyan N, Rudolf G, Ruszczyński A (2006) Relaxations of linear programming problems with first order stochastic dominance constraints. Oper Res Lett 34(6):653–659

    MathSciNet  MATH  Google Scholar 

  • Obrecht M, Knez M (2017) Carbon and resource savings of different cargo container designs. J Clean Prod 155(1):151–156

    Google Scholar 

  • Pflug G (2000) Some remarks on the value-at-risk and the conditional value-at-risk. Probab Const Optim 49:272–281

    MathSciNet  MATH  Google Scholar 

  • Pierre C, Francesco P, Theo N (2019) Towards low carbon global supply chains: a multi-trade analysis of \(CO_2\) emission reductions in container shipping. Int J Prod Econ 208:17–28

    Google Scholar 

  • Pour A, Azimi Z, Salari M (2017) Sample average approximation method for a new stochastic personnel assignment problem. Comput Ind Eng 113:135–143

    Google Scholar 

  • Quddus M, Chowdhury S, Marufuzzaman M, Yu F, Bian F (2018) A two-stage chance-constrained stochastic programming model for a bio-fuel supply chain network. Int J Prod Econ 195:27–44

    Google Scholar 

  • Rockafellar R, Uryasev S (2000) Optimization of conditional value-at-risk. J Risk 2(3):21–41

    Google Scholar 

  • Shen S (2014) Using integer programming for balancing return and risk in problems with individual chance constraints. Comput Oper Res 49:59–70

    MathSciNet  MATH  Google Scholar 

  • Sim J (2018) A carbon emission evaluation model for a container terminal. J Clean Prod 186:526–533

    Google Scholar 

  • Singh V, Lisser A (2019) A second-order cone programming formulation for two player zero-sum games with chance constraints. Eur J Oper Res 275(3):839–845

    MathSciNet  MATH  Google Scholar 

  • Sun H, Gao Z, Szeto WY, Long J, Zhao F (2014) A distributionally robust joint chance constrained optimization model for the dynamic network design problem under demand uncertainty. Netw Spat Econ 14(3–4):409–433

    MathSciNet  MATH  Google Scholar 

  • Tavakoli M, Shokridehaki F, Akorede M, Marzband M, Vechiu I, Pouresmaeil E (2018) CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int J Electr Power Energy Syst 100:1–9

    Google Scholar 

  • Urgo M (2019) A branch-and-bound approach to schedule a no-wait flow shop to minimize the CVaR of the residual work content. Comput Ind Eng 129:67–75

    Google Scholar 

  • Wagner M (2008) Stochastic 0–1 linear programming under limited distributional information. Oper Res Lett 36(2):150–156

    MathSciNet  MATH  Google Scholar 

  • Wang C, Huang H (2016) Optimal insurance contract under VaR and CVaR constraints. N Am J Econ Finance 37:110–127

    Google Scholar 

  • Wang H, Zhang X, Wang S (2016) A joint optimization model for liner container cargo assignment problem using state-augmented shipping network framework. Transp Res Part C 68:425–446

    Google Scholar 

  • Wang S, Qu X, Wang T, Yi W (2017) Optimal container routing in liner shipping networks considering repacking 20 ft containers into 40 ft containers. J Adv Transp 2017:1–9

    Google Scholar 

  • Wang S (2013) Essential elements in tactical planning models for container liner shipping. Transp Res Part B 54(1):84–99

    Google Scholar 

  • Wright L, Williams I (2011) Carbon footprinting: towards a university accepted definition. Carb Manag 2:61–72

    Google Scholar 

  • Xie Y, Song D (2018) Optimal planning for container prestaging, discharging, and loading processes at seaport rail terminals with uncertainty. Transp Res Part E 119:88–109

    Google Scholar 

  • Xue W, Ma L, Shen H (2015) Optimal inventory and hedging decisions with CVaR consideration. Int J Prod Econ 162:70–82

    Google Scholar 

  • Yun Y, Lee M, Seok Y (2011) Optimal inventory control of empty containers in inland transportation system. Int J Prod Econ 133(1):451–457

    Google Scholar 

  • Zhang Y, Shen S, Erdogan S (2017a) Solving 0-1 semidefinite programs for distributionally robust allocation of surgery blocks, Social Science Electronic Pubishing, SSRN: https://ssrn.com/abstract=2997524

  • Zhen L, Hu Y, Wang S, Laporte G, Wu Y (2019) Fleet deployment and demand fulfillment for container shipping liners. Transp Res Part B 120:15–32

    Google Scholar 

  • Zymler S, Kuhn D, Rustem B (2013) Distributionally robust joint chance constraints with second-order moment information. Math Program 137(1–2):167–198

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for their constructive comments. This work was supported by National Natural Science Foundation of China (NSFC) under Grants 71531011, 71871159, 71771048, 71832001 and 71571134. This work was also sponsored by Shanghai Pujiang Program (17PJC046).

Author information

Authors and Affiliations

  1. School of Economics and Management, Tongji University, Shanghai, 200092, China

    Ming Liu & Rongfan Liu

  2. School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai, 200433, China

    E Zhang

  3. ESIEE Paris, Université Paris-Est, 93162, Noisy-le-Grand, France

    Chengbin Chu

Authors
  1. Ming Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rongfan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chengbin Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, M., Liu, R., Zhang, E. et al. Eco-friendly container transshipment route scheduling problem with repacking operations. J Comb Optim 43, 1010–1035 (2022). https://doi.org/10.1007/s10878-020-00619-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10878-020-00619-8

Keywords

Search

Navigation