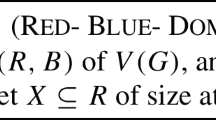Abstract
In this paper, we study the parameterized complexity of Dominating Set problem in chordal graphs and near chordal graphs. We show the problem is W[2]-hard and cannot be solved in time n o(k) in chordal and s-chordal (s>3) graphs unless W[1]=FPT. In addition, we obtain inapproximability results for computing a minimum dominating set in chordal and near chordal graphs. Our results prove that unless NP=P, the minimum dominating set in a chordal or s-chordal (s>3) graph cannot be approximated within a ratio of \(\frac{c}{3}\ln{n}\) in polynomial time, where n is the number of vertices in the graph and 0<c<1 is the constant from the inapproximability of the minimum dominating set in general graphs. In other words, our results suggest that restricting to chordal or s-chordal graphs can improve the approximation ratio by no more than a factor of 3. We then extend our techniques to find similar results for the Independent Dominating Set problem and the Connected Dominating Set problem in chordal or near chordal graphs.
Similar content being viewed by others
References
Alber J, Fellows MR, Niedermeier R (2004) Polynomial-time data reduction for dominating set. J ACM 51(3):363–384
Baker BS (1994) Approximation algorithms for NP-complete problems on planar graphs. J ACM 41(1):153–180
Chen J, Kanj IA, Jia W (2001) Vertex cover: further observations and further improvements. J Algorithms 41:280–301
Chen J, Huang X, Kanj IA, Xia G (2004) Linear FPT reductions and computational lower bounds. In: Proceedings of the thirty-sixth ACM symposium on theory of computing (STOC 2004), pp 212–221
Chen J, Fernau H, Kanj IA, Xia G (2007) Parametric duality and lower bounds and upper bounds on Kernel size. SIAM J Comput 37(4):1077–1106
Chlebík M, Chlebíkova J (2004) Approximation hardness of dominating set problems. In: Proceedings of 12th annual European symposium on algorithms. LNCS, vol 3221. Springer, Berlin, pp 192–203
Dinur I, Safra S (2002) The importance of being biased. In: Proceeding of the thirty-fourth ACM symposium on theory of computing (STOC 2002), pp 33–42
Downey RG, Fellows MR (1995) Fixed parameter tractability and completeness i: basic theory. SIAM J Comput 24:873–921
Downey RG, Fellows MR (1998) Parameterized complexity. Springer, Berlin
Fanica G (1974) The intersection graphs of subtrees in trees are exactly the chordal graphs. J Comb Theory, Ser B 16:47–56
Farber M (1982) Independent domination in chordal graphs. Oper Res Lett 1:134–138
Garey MR, Johnson DS (1979) Computers and intractability. Series of books in the mathematical sciences. Freeman, New York. A guide to the theory of NP-completeness
Grötschel M, Lovász L, Schrijver A (1981) The ellipsoid method and its consequences in combinatorial optimization. Combinatorica I(2):169–197
Halldórson MM (1993) Approximating the minimum maximal independence number. Inf Process Lett 46:169–172
Johnson DS (1974) Approximate algorithms for combinatorial problems. J Comput Syst Sci 9:256–278
Liu C, Song Y (2009) Parameterized dominating set problem in chordal graphs: complexity and lower bound. J Comb Optim 18(1):87–97
Lokshtanov D, Mnich M, Saurabh S (2009) Linear Kernel for planar connected dominating set. In: Proceedings of the sixth annual conference on theory and applications of models of computation (TAMC 2009), pp 281–290
Orlovich YL, Gordon VS, de Werra D (2009) On the inapproximability of independent domination in 2P 3-free perfect graphs. Theor Comput Sci 410(8–10):977–982
Raz R, Safra S (1997) A sub-constant error-probability low degree test, and a sub-constant error-probability PCP characterization of NP. In: Proceedings of the twenty-ninth ACM symposium on theory of computing (STOC 1997), pp 475–484
Yang S, Wu J, Cardei M, Dai F (2006) Extended dominating set and its applications in ad hoc networks using cooperative communication. IEEE Trans Parallel Distrib Comput 17(8):851–864
Zhu J (2009) Approximation for minimum dominating set. In: Proceedings of the 2nd international conference on interaction sciences: information technology, culture and human, pp 119–124
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Liu, C., Song, Y. Parameterized complexity and inapproximability of dominating set problem in chordal and near chordal graphs. J Comb Optim 22, 684–698 (2011). https://doi.org/10.1007/s10878-010-9317-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-010-9317-7