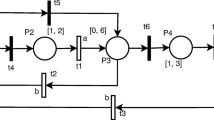
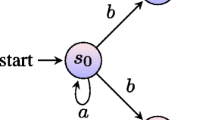
Abstract
In this paper we deal with the problem of estimating the marking of a labeled Petri net with nondeterministic transitions. In particular, we consider the case in which nondeterminism is due to the presence of transitions that share the same label and that can be simultaneously enabled. Under the assumption that: the structure of the net is known, the initial marking is known, the transition labels can be observed, the nondeterministic transitions are contact-free, we present a technique for characterizing the set of markings that are consistent with the actual observation. More precisely, we show that the set of markings consistent with an observed word can be represented by a linear system with a fixed structure that does not depend on the length of the observed word.
Similar content being viewed by others
References
Benasser, A. 2000. In Reachability in Petri nets: an approach based on constraint programming, (Ph.D. Thesis), France, Université de Lille, (in French).
Caines, P. E., and Wang, S. 1989. Classical and logic based regulator design and its complexity for partially observed automata. In 28th Int. Conf. Decis. Control, Tampa, Florida, pp. 132–137.
Caines, P. E., Greiner, R., and Wang, S. 1988. Dynamical logic observers for finite automata. In 27th Conf. Decis. Control, Austin, Texas, pp. 226–233.
Gaubert, S., and Giua, A. 1999. Petri net languages and infinite subsets of \(\mathbb{N}^{m} \). J. Comp. Syst. Sci. 59(3): 373–391.
Giua, A., and Seatzu, C. 2002. Observability of place/transition nets. IEEE Trans. Automat. Contr. 47(9): 1424–1437.
Giua, A., Júlvez, J., and Seatzu, C. 2003. Marking estimation of Petri nets with λ-free labeling. In Proc. Workshop on Discrete Event Systems Control, Eindhoven, The Netherlands, pp. 75–95. Workshop Revised version: “Marking estimation of Petri nets with pairs of nondeterministic transitions.” Asian J. Control, Special Issue on the “Control of Discrete Event Systems” 6(2): 270–280, 2004.
Giua, A., Seatzu, C., and Basile, F. 2004a. Observer based state-feedback control of timed Petri nets with deadlock recovery. IEEE Trans. Automat. Contr. 49(1): 17–29.
Giua, A., Corona, D., and Seatzu, C. 2004b. Marking estimation of Petri nets with silent transitions. 2004 IEEE Int. Conf. Decis. Control (to appear).
Kumar, R., Garg, V., and Markus, S. I. 1993. Predicates and predicate transformers for supervisory control of discrete event dynamical systems. IEEE Trans. Automat. Contr. 38(2): 232–247.
Meda, M. E., Ramírez, A., and Malo, A. 1998. Identification in discrete event systems. In IEEE Int. Conf. Syst. Man Cybern., San Diego, California, pp. 740–745.
Murata, T. 1989. Petri nets: Properties, analysis and applications. Proc. IEEE 77(4): 541–580.
Özveren, C. M., and Willsky, A. S. 1990. Observability of discrete event dynamic systems. IEEE Trans. Automat. Contr. 35(7): 797–806.
Peterson, J. L. 1981. Petri net theory and the modeling of systems. Prentice-Hall, 1981.
Ramadge, P. J. 1986. Observability of discrete-event systems. In 25th Int. Conf. Decis. Contr., Athens, Greece, pp. 1108–1112.
Zhang, L., and Holloway, L. E. 1995. Forbidden state avoidance in controlled Petri nets under partial observation. In 33rd Allerton Conf., Monticello, Illinois, pp. 146–155.
Author information
Authors and Affiliations
Corresponding author
Additional information
*Contact author is Alessandro Giua.
Rights and permissions
About this article
Cite this article
Giua, A., Corona, D. & Seatzu, C. State Estimation of λ-free Labeled Petri Nets with Contact-Free Nondeterministic Transitions*. Discrete Event Dyn Syst 15, 85–108 (2005). https://doi.org/10.1007/s10626-005-5239-4
Issue Date:
DOI: https://doi.org/10.1007/s10626-005-5239-4