Abstract
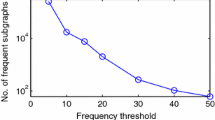
A significant number of applications require effective and efficient manipulation of relational graphs, towards discovering important patterns. Some example applications are: (i) analysis of microarray data in bioinformatics, (ii) pattern discovery in a large graph representing a social network, (iii) analysis of transportation networks, (iv) community discovery in Web data. The basic approach followed by existing methods is to apply mining techniques on graph data to discover important patterns, such as subgraphs that are likely to be useful. However, in some cases the number of mined patterns is large, posing difficulties in selecting the most important ones. For example, applying frequent subgraph mining on a set of graphs the system returns all connected subgraphs whose frequency is above a specified (usually user-defined) threshold. The number of discovered patterns may be large, and this number depends on the data characteristics and the frequency threshold specified. It would be more convenient for the user if “goodness” criteria could be set to evaluate the usefulness of these patterns, and if the user could provide preferences to the system regarding the characteristics of the discovered patterns. In this paper, we propose a methodology to support such preferences by applying subgraph discovery in relational graphs towards retrieving important connected subgraphs. The importance of a subgraph is determined by: (i) the order of the subgraph (the number of vertices) and (ii) the subgraph edge connectivity. The performance of the proposed technique is evaluated by using real-life as well as synthetically generated data sets.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Behzad M, Chartrand G, Lesniak-Foster L (1979) Graphs and digraphs. Pindle, Weber & Schmidt, Boston
Bell MGH, Iida Y (1997) Transportation network analysis. Wiley, London
Borzsonyi S, Kossmann D, Stocker K (2001) The Skyline operator. In: Proceedings of the 17th international conference on data engineering, pp 421–430
Chartrand G (1966) A graph-theoretic approach to a communications problem. SIAM J Appl Math 14(5): 778–781
Cook, DJ, Holder, LB (eds) (2007) Mining graph data. Wiley, London
Flake GW, Lawrence S, Giles CL (2000) Efficient identification of Web communities. In: Proceedings of the ACM KDD conference, pp 150–160
Gibson D, Kumar R, Tomkins A (2005) Discovering large dense subgraphs in massive graphs. In: Proceedings of the 31st VLDB conference, pp 721–732
Gross J, Yellen J (1999) Graph theory and its applications. CRC Press, Boca Raton
Hao J, Orlin JB (1992) A faster algorithm for finding the minimum cut in a graph. In: Proceedings of the 3rd ACM-SIAM symposium on discrete algorithms, pp 165–174
Hartuv E, Shamir R (2000) A clustering algorithm based on graph connectivity. Inform Process Lett 76: 175–181
Hu H, Yan X, Huang Y, Han J, Zhou XJ (2005) Mining coherent dense subgraphs across massive biological networks for functional discovery. Bioinformatics 21(1): i213–i221
Karger DR (1996) Minimum cuts in near-linear time. In: Proceedings of ACM STOC, pp 56–63
Matula DW (1987) Determining edge connectivity in O(m·n). In: Proceedings of the 28th symposium on foundations of computer science, pp 249–251
Nagamochi H, Ibaraki T (1992) Computing edge-connectivity in multigraphs and capacitated graphs. SIAM J Discrete Math 5: 54–66
Papadias D, Tao Y, Fu G, Seeger B (2005) Progressive skyline computation in database systems. ACM Trans Database Syst 30(1): 41–82
Stoer M, Wagner F (1997) A simple min-cut algorithm. J ACM 44(4): 585–591
Wang JTL, Zaki MJ, Toivonen HTT, Shasha D (eds) (2005) Data mining in bioinformatics. Springer
Wasserman S, Faust K (1994) Social network analysis: methods and applications. Cambridge University Press, Cambridge
Whitney H (1932) Congruent graphs and the connectivity of graphs. Am J Math 54: 150–168
Wolle T, Koster AMCA, Bodlaender HL (2004) A note on contraction degeneracy. Technical Report UU-CS-2004-042, Utrecht University
Wu Z, Leahy R (1993) An optimal graph theoretic approach to data clustering: theory and its application to image segmentation. IEEE Trans Pattern Anal Machine Intell 15(11): 1101–1113
Yan X, Mehan MR, Huang Y, Waterman MS, Yu PS, Zhou XJ (2007) A graph-based approach to systematically reconstruct human transcriptional regulatory modules. Bioinformatics 23(13): i577–i586
Yan X, Zhou XJ, Han J (2005) Mining closed relational graphs with connectivity constraints. In: Proceedings of ACM KDD conference, pp 324–333
Zhu F, Yan X, Han J, Yu PS (2007) gPrune: a constraint pushing framework for graph pattern mining. In: Proceedings of PAKDD conference, pp 388–400
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editors: Walter Daelemans, Bart Goethals, and Katharina Morik.
Rights and permissions
About this article
Cite this article
Papadopoulos, A.N., Lyritsis, A. & Manolopoulos, Y. SkyGraph: an algorithm for important subgraph discovery in relational graphs. Data Min Knowl Disc 17, 57–76 (2008). https://doi.org/10.1007/s10618-008-0109-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-008-0109-y