Abstract
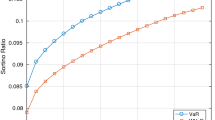
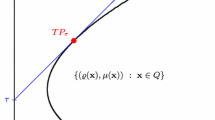
This note is focused on computational efficiency of the portfolio selection models based on the Conditional Value at Risk (CVaR) risk measure. The CVaR measure represents the mean shortfall at a specified confidence level and its optimization may be expressed with a Linear Programming (LP) model. The corresponding portfolio selection models can be solved with general purpose LP solvers. However, in the case of more advanced simulation models employed for scenario generation one may get several thousands of scenarios. This may lead to the LP model with huge number of variables and constraints thus decreasing the computational efficiency of the model. To overcome this difficulty some alternative solution approaches are explored employing cutting planes or nondifferential optimization techniques among others. Without questioning importance and quality of the introduced methods we demonstrate much better performances of the simplex method when applied to appropriately rebuilt CVaR models taking advantages of the LP duality.
Similar content being viewed by others
References
Andersson, F., Mausser, H., Rosen, D., Uryasev, S.: Credit risk optimization with conditional value-at-risk criterion. Math. Program. 89, 273–291 (2001)
Fabian, C.I., Mitra, G., Roman, D.: Processing second order stochastic dominance models using cutting plane representations. Math. Program. doi:10.1007/s10107-009-0326-1
Guastaroba, G., Mansini, R., Speranza, M.G.: On the effectiveness of scenario generation techniques in single-period portfolio optimization. Eur. J. Oper. Res. 192, 500–511 (2009)
IBM ILOG CPLEX 12.1—Parameters Reference Manual. Information available at http://www.ilog.com (2009)
Konno, H., Waki, H., Yuuki, A.: Portfolio optimization under lower partial risk measures. Asia-Pac. Financ. Mark. 9, 127–140 (2002)
Krzemienowski, A., Ogryczak, W.: On extending the LP computable risk measures to account downside risk. Comput. Optim. Appl. 32, 133–160 (2005)
Künzi-Bay, A., Mayer, J.: Computational aspects of minimizing conditional value-at-risk. Comput. Manag. Sci. 3, 3–27 (2006)
Lim, C., Sherali, H.D., Uryasev, S.: Portfolio optimization by minimizing conditional value-at-risk via nondifferentiable optimization. Comput. Optim. Appl. doi:10.1007/s10589-008-9196-3
Mansini, R., Ogryczak, W., Speranza, M.G.: Conditional value at risk and related linear programming models for portfolio optimization. Ann. Oper. Res. 152, 227–256 (2007)
Miller, N., Ruszczyński, A.: Risk-adjusted probability measures in portfolio optimization with coherent measures of risk. Eur. J. Oper. Res. 191, 193–206 (2008)
Ogryczak, W., Ruszczyński, A.: Dual stochastic dominance and related mean-risk models. SIAM J. Optim. 13, 60–78 (2002)
Ogryczak, W., Śliwiński, T.: On efficient optimization of the CVaR and related LP computable risk measures for portfolio selection. In: International Conference on Mathematical and Statistical Methods for Actuarial Science and Finance MAF 2008, Venice, Italy (2008). http://maf2008.unive.it/viewabstract.php?id=38
Pflug, G.Ch.: Scenario tree generation for multiperiod financial optimization by optimal discretization. Math. Program. 89, 251–271 (2001)
Rockafellar, R.T., Uryasev, S.: Optimization of conditional value-at-risk. J. Risk 2, 21–41 (2000)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ogryczak, W., Śliwiński, T. On solving the dual for portfolio selection by optimizing Conditional Value at Risk. Comput Optim Appl 50, 591–595 (2011). https://doi.org/10.1007/s10589-010-9321-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-010-9321-y