Analysis on key dimension’s measurement error in high speed computing | Cluster Computing
Skip to main content
Springer Nature Link
Log in

Analysis on key dimension’s measurement error in high speed computing

  • Published:
Cluster Computing Aims and scope Submit manuscript

Abstract

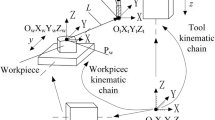
HSK shank is the most widely used shank in high speed machining recently, the key dimensions’ measurement technology of which decides the level of its manufacture precision. How to accomplish the dimensions’ measurement for HSK shank quickly and accurately is crucial for improving its manufacture level. In order to solve this problem, a kind of special measuring gauge for HSK shank is developed. A novel and simple positioning device is developed according to the idea of limiting shank’s degrees of freedom, which is the most important component and affects measuring precision greatly. It is pointed out that positioning device is a major factor which leads to the generation of system error. By means of theoretical analysis and computing errors derived from various deviation of each transducer relative to its theoretical installing location are studied in detail, by experimental measuring and data computing random errors are analyzed accurately. Error transmission on indirectly measured dimension and measurement standard uncertainty of key dimensions are studied respectively. Research shows that measuring precision of the gauge meets the requirement of high-precision measurement for HSK shank’s key dimensions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Yang, Y., Zhang, W.H., Ma, Y.C., Wan, M.: Generalized method for the analysis of bending, torsional and axial receptances of tool-holder-spindle assembly. Int. J. Mach. Tools Manuf. 99, 48–67 (2015)

    Article  Google Scholar 

  2. Gilovoi, L.Ya., Molodtsov, V.V.: Influence of centrifugal forces on the operation of HSK couplings. Russ. Eng. Res. 32(3), 276–281 (2012)

    Article  Google Scholar 

  3. Jie, W.K., Chen, J., Zheng, D.S., Wang, G.C.: The coupling characteristic of HSK tool-holder/spindle interface for high-speed NC machine tool. Appl. Mech. Mater. 590, 121–125 (2014)

    Article  Google Scholar 

  4. Zhang, G., Zhang, Y., Lü, F., Xiu, S.: Analysis on HSK toolholder-spindle interface at high rotational speed for CNC machine tools. China Mech. Eng. 23(6), 631–635 (2012)

    Google Scholar 

  5. Kim, K., Kim, J.: Dynamic displacement measurement of a vibratory object using a terrestrial laser scanner. Meas. Sci. Technol. 26(4), 45002–45012 (2015)

    Article  Google Scholar 

  6. Kondo, Y., Hasegawa, K., Kawamata, H., Morishita, T., Naito, F.: On-machine non-contact dimension-measurement system with laser displacement sensor for vane-tip machining of RFQs. Nucl. Instrum. Methods Phys. Res. 667(5), 5–10 (2012)

    Article  Google Scholar 

  7. Shiramatsu, T., Kitano, K., Kawada, M., Mitsui, K.: Development of measurement method for shape and dimension of micro-components. Jpn. J. Appl. Phys. 51(47), 369–376 (2012)

    Google Scholar 

  8. Kwon, Y., Hong, J.: Integrated remote control of the process capability and the accuracy of vision calibration. Robot. Computer-Integr. Manuf. 30, 451–459 (2014)

    Article  Google Scholar 

  9. Zhao, Z.Y., Zhu, J.G., Xue, B., Yang, L.H.: Optimization for calibration of large-scale optical measurement positioning system by using spherical constraint. J. Opt. Soc. Am. A 31(7), 1427–1435 (2014)

    Article  Google Scholar 

  10. Ibaraki, S., Iritani, T., Matsushita, T.: Calibration of location errors of rotary axes on five-axis machine tools by on-the-machine measurement using a touch-trigger probe. Int. J. Mach. Tools Manuf. 580, 44–53 (2012)

    Article  Google Scholar 

  11. Lee, K., Lee, D.M., Yang, S.H.: Parametric modeling and estimation of geometric errors for a rotary axis using double ball-bar. Int. J. Adv. Manuf. Technol. 62(5), 741–750 (2012)

    Article  Google Scholar 

  12. Yuen, K.V.: Updating large models for mechanical systems using incomplete modal measurement. Mech. Syst. Signal Process. 28(2), 297–308 (2012)

    Article  Google Scholar 

  13. You, H., Yang, J.: Development of an analysis system for geometric contour error evaluation in ultra-precision machining for microlens arrays. J. Mech. Sci. Technol. 28(10), 4121–4129 (2014)

    Article  Google Scholar 

  14. Lee, J.C., Lee, K.I., Yang, S.H.: Development of compact three-degrees-of-freedom compensation system for geometric errors of an ultra-precision linear axis. Mech. Mach. Theory 99, 72–82 (2016)

    Article  Google Scholar 

  15. Yang, Z., Hong, J., Zhang, J.H.: Research on the rotational accuracy measurement of an aerostatic spindle in a rolling bearing performance analysis instrument. Int. J. Precis. Eng. Manuf. 15(7), 1293–1302 (2014)

    Article  Google Scholar 

  16. Ashok, S.D., Samuel, G.L.: Modeling, measurement, and evaluation of spindle radial errors in a miniaturized machine tool. Int. J. Adv. Manuf. Technol. 59(5), 445–461 (2012)

    Article  Google Scholar 

  17. Soori, M., Arezoo, B., Habibi, M.: Dimensional and geometrical errors of three-axis CNC milling machines in a virtual machining system. Computer-Aided Des. 45(11), 1306–1313 (2013)

    Article  Google Scholar 

  18. Anandan, K.P., Tulsian, A.S., Donmez, A., Ozdoganlar, O.B.: A Technique for measuring radial error motions of ultra-high-speed miniature spindles used for micromachining. Precis. Eng. 36(1), 104–120 (2012)

    Article  Google Scholar 

  19. Matekar, S.B., Gogate, G.R.: Optimum synthesis of path generating four-bar mechanisms using differential evolution and a modified error function. Mech. Mach. Theory 52(3), 158–179 (2012)

    Article  Google Scholar 

  20. Gogate, G.R., Matekar, S.B.: Optimum synthesis of motion generating four-bar mechanisms using alternate error functions. Mech. Mach. Theory 54(4), 41–61 (2012)

    Article  Google Scholar 

  21. Luo, X.B., Fan, H.Q., Song, Z.Y., Fu, Q.: Bernoulli particle filter with observer altitude for maritime radiation source tracking in the presence of measurement uncertainty. Chin. J. Aeronaut. 26(6), 1459–1470 (2013)

    Article  Google Scholar 

  22. Aggogeri, F., Barbato, G., Barini, E.M., Genta, G., Levi, R.: Measurement uncertainty assessment of coordinate measuring machines by simulation and planned experimentation. Cirp J. Manuf. Sci. Technol. 4(1), 51–56 (2011)

    Article  Google Scholar 

  23. Koviljka, Stankovi: Influence of the plain-parallel electrode surface dimensions on the type A measurement uncertainty of GM counter. Nucl. Technol. Radiat. Prot. 26(1), 39–44 (2011)

    Article  Google Scholar 

  24. Lee, K., Yang, S.H.: Robust measurement method and uncertainty analysis for position-independent geometric errors of a rotary axis using a double ball-bar. Int. J. Precis. Eng. Manuf. 14(2), 231–239 (2013)

    Article  Google Scholar 

Download references

Acknowledgements

This research has been financially supported by the National Natural Science Foundation of China under Grant Nos. 51275217.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Jiangsu University, Zhenjiang, 212013, Jiangsu, China

    Jin Zhang & Shulin Wang

  2. School of Mechanical Engineering, Yangzhou Polytechnic College, Yangzhou, 225009, Jiangsu, China

    Jin Zhang & Yijun Zhou

Authors
  1. Jin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shulin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yijun Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jin Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, J., Wang, S. & Zhou, Y. Analysis on key dimension’s measurement error in high speed computing. Cluster Comput 22 (Suppl 1), 769–779 (2019). https://doi.org/10.1007/s10586-017-1241-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10586-017-1241-5

Keywords

Search

Navigation