Semi-supervised bi-orthogonal constraints dual-graph regularized NMF for subspace clustering | Applied Intelligence Skip to main content
Springer Nature Link
Log in

Semi-supervised bi-orthogonal constraints dual-graph regularized NMF for subspace clustering

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

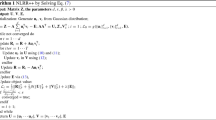
Non-negative matrix factorization (NMF), as an explanatory feature extraction technology, has powerful dimensionality reduction and semantic representation capabilities. In recent years, it has attracted great attention in the process of dimensionality reduction analysis of real high-dimensional data. However, the classic NMF algorithm is an unsupervised method in terms of learning methods. In the calculation process, the spatial structure information in the original data is often ignored, resulting in poor clustering performance of the algorithm in the subspace. In order to overcome the above problems, this paper proposes a semi-supervised NMF algorithm called semi-supervised dual graph regularized NMF with biorthogonal constraints (SDGNMF-BO). In this algorithm, the semi-supervised NMF three-factor decomposition is based on the dual graph model of the data space and feature space of the original data, which can effectively improve the learning ability of the algorithm in the subspace, and the biorthogonal constraint conditions are added in the decomposition process and achieve better local representation, significantly reduce the inconsistency between the original matrix and the basic vector. In order to prove the superiority of the algorithm under fair conditions, compares the multi-directional clustering experiments of 4 real image data sets and 1 text data set, and uses 2 clustering evaluation indexes to prove that the algorithm is better than other comparison algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Liu Z, Wang X, Pu J, Wang L, Zhang L (2017) Nonnegative low-rank representation based manifold embedding for semi-supervised learning. Knowl-Based Syst 136:121–129

    Article  Google Scholar 

  2. Zheng K, Wang X (2018) Feature selection method with joint maximal information entropy between features and class. Patt Recogn 77:20–29

    Article  Google Scholar 

  3. Xin X, Wang J, Xie R, Zhou S, Huang W, Zheng N (2019) Semisupervised person re-identification using multi-view clustering. Patt Recogn 88:285–297

    Article  Google Scholar 

  4. Huang Q, Yin X, Chen S, Wang Y, Chen B (2020) Robust nonnegative matrix factorization with structure regularization. Neurocomputing 412

  5. Liu X, Wang J, Cheng D, Shi D, Zhang Y (2020) Non-convex low-rank representation combined with rank-one matrix sum for subspace clustering. Soft Comput 412

  6. Lee D, Seung H (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401(6755):788—791

    Article  Google Scholar 

  7. Lee D, Seung H (2001) Algorithms for non-negative matrix factorization. Adv Neural Inf Process Sys 13:556–562

    Google Scholar 

  8. Hoyer PQ (2004) Non-negative matrix factorization with sparseness constrains. J Mach Learn Res, 5(9):1457–1469

  9. Hayashi T, Fujita H (2020) Cluster-based zero-shot learning for multivariate data. J Amb Intell Human Comput 12:1897–1911

  10. Shu Z, Weng Z, Zhang Y, You C, Liu Z (2020) Graph regularized constrained non-negative matrix factorization with lp smoothness for image representation. IEEE Access 8:133777–133786

    Article  Google Scholar 

  11. Sun F, Xu M, Hu X, Jiang X (2016) Graph regularized and sparse nonnegative matrix factorization with hard constraints for data representation. Neurocomputing 173

  12. Jia Y, Liu H, Hou J, Sam K (2020) Semisupervised adaptive symmetric non-negative matrix factorization. IEEE Trans Cybern 1–1

  13. Liu H, Wu Z, Li X (2012) Constrained non-negative matrix factorization for image representation. IEEE Trans Patt Anal Mach 34(7):1299–1311

    Article  Google Scholar 

  14. Cai D, He X, Han J (2011) Graph regularized non-negative matrix factorization for data representation. IEEE Trans Patt Anal Mach Intell 33(8):1548–1560

    Article  Google Scholar 

  15. Meng Y, Shang R, Jiao L, Zhang W, Yang S (2018) Dual-graph regularized non-negative matrix factorization with sparse and orthogonal constraints. Eng Appl Artif Intell 69:24–35

    Article  Google Scholar 

  16. Peng S, Ser W, Chen B, Lin Z (2021) Robust semi-supervised nonnegative matrix factorization for image clustering. Patt Recogn 111:107683

    Article  Google Scholar 

  17. Zhang L, Liu Z, Pu J, Song B (2019) Adaptive graph regularized nonnegative matrix factorization for data representation. Appl Intell 50(2):438–447

    Article  Google Scholar 

  18. Teng X, Lan L, Zhang X (2020) Transductive nonnegative matrix tri-factorization. IEEE Access 8:81331–81347

    Article  Google Scholar 

  19. Li H, Zhang J, Hu J, Zhang C, Liu J (2016) Graph-based discriminative concept factorization for data representation. Knowl-Based Syst 118

  20. Zhang G, Ma Z, Huang H (2020) Dimensionality reduction of tensors based on local homeomorphism and global subspace projection distance minimum. IEEE Access 8:116064–116077

    Article  Google Scholar 

  21. Meng Y, Shang R, Jiao L, Zhang W, Yuan Y, Yang S (2018) Feature selection based dual-graph sparse non-negative matrix factorization for local discriminative clustering. Neurocomputing 290:87–99

    Article  Google Scholar 

  22. Li Z, Wu X, Peng H (2010) Nonnegative matrix factorization on orthogonal subspace. Patt Recogn Lett 31:905–911

    Article  Google Scholar 

  23. Rahiche A, Cheriet M (2020) Forgery detection in hyperspectral document images using graph orthogonal nonnegative matrix factorization. IEEE Int Conf Comput Vis Patt Recogn 2823–2831

  24. Fan S, Jia Q, Cheng W (2020) Safety monitoring by a graph-regularized semi-supervised nonnegative matrix factorization with applications to a vision-based marking process. IEEE Access 8:112278–112286

    Article  Google Scholar 

  25. Pei X, Chen C, Guan Y (2017) joint sparse representation and embedding propagation learning: a framework for graph- based semisupervised learning. IEEE Trans Neural Netw Learn Sys 1–12

  26. Shang R, Wang W, Rustam S, Jiao L (2016) Subspace learning-based graph regularized feature selection. Knowl-Based Syst 112:152–165

    Article  Google Scholar 

  27. Li G, Zhang X, Zheng S, Li D (2017) Semi-supervised convex nonnegative matrix factorizations with graph regularized for image representation. Neurocomputing 237:1–11

    Article  Google Scholar 

  28. Yi Y, Qiao S, Zhou W (2018) Adaptive multiple graph regularized semi-supervised extreme learning machine. Soft Comput 22:3545–3562

    Article  Google Scholar 

  29. Babaee M, Tsoukalas S, Babaee M (2015) Discriminative nonnegative matrix factorization for dimensionality reduction. Neurocomputing 173:212–223

    Article  Google Scholar 

  30. Zheng M, Bu J, Chen C A (2011) Graph regularized sparse coding for image representation. IEEE Trans Image Process 20(5):1327–1336

    Article  MathSciNet  Google Scholar 

  31. Shang F, Jiao L, Wang F (2012) Graph dual regularization non-negative matrix factorization for co-clustering. Patt Recogn 45(6):2237–2250

    Article  Google Scholar 

  32. Gillis N, Glineur F (2012) Accelerated multiplicative updates and hierarchical ALS algorithms for nonnegative matrix factorization. Neural Comput 24(4):1085–1105

    Article  MathSciNet  Google Scholar 

  33. Shiga M, Tatsumi K, Muto S (2016) Sparse modeling of EELS and EDX spectral imaging data by nonnegative matrix factorization. Ultramicroscopy 170:43–59

    Article  Google Scholar 

  34. Qian W, Hong B, Cai D, He X, Li X (2016) Non-negative matrix factorization with sinkhorn distance. Int Conf Artif Intell

  35. Zhang Y, Yang Y, Li T, Fujita H (2019) A multitask multiview clustering algorithm in heterogeneous situations based on lle and le. Knowl-Based Syst 163(1):776–786

    Article  Google Scholar 

  36. Wang H, Yang Y, Liu B, Fujita H (2019) A study of graph-based system for multi-view clustering. Knowl Based Sys 163:1009–1019

    Article  Google Scholar 

Download references

Acknowledgements

This work was funded by the National Natural Science Foundation of China,under Grant 51774219, Hubei Province Announcement System Science and Technology Project under grant 2020BED003, Key R&D Projects in Hubei Province under grant 2020BAB098.

Author information

Authors and Affiliations

  1. School of Information Science and Engineering, Wuhan University of Science and Technology, 947 Peace Avenue, Qingshan district, Wuhan, People’s Republic of China

    SongTao Li, WeiGang Li, JunWei Hu & Yang Li

  2. Engineering Research Center for Metallurgical Automation and Measurement Technology, Ministry of Education, Wuhan University of Science and Technology, 947 Peace Avenue, Qingshan district, Wuhan, People’s Republic of China

    SongTao Li, WeiGang Li, JunWei Hu & Yang Li

Authors
  1. SongTao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. WeiGang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. JunWei Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to WeiGang Li.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, S., Li, W., Hu, J. et al. Semi-supervised bi-orthogonal constraints dual-graph regularized NMF for subspace clustering. Appl Intell 52, 3227–3248 (2022). https://doi.org/10.1007/s10489-021-02522-z

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-021-02522-z

Keywords

Search

Navigation