Oversampling technique based on fuzzy representativeness difference for classifying imbalanced data | Applied Intelligence
Skip to main content
Springer Nature Link
Log in

Oversampling technique based on fuzzy representativeness difference for classifying imbalanced data

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

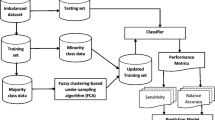
Class imbalance problem poses a difficulty to learning algorithms in pattern classification. Oversampling techniques is one of the most widely used techniques to solve these problems, but the majority of them use the sample size ratio as an imbalanced standard. This paper proposes a fuzzy representativeness difference-based oversampling technique, using affinity propagation and the chromosome theory of inheritance (FRDOAC). The fuzzy representativeness difference (FRD) is adopted as a new imbalance metric, which focuses on the importance of samples rather than the number. FRDOAC firstly finds the representative samples of each class according to affinity propagation. Secondly, fuzzy representativeness of every sample is calculated by the Mahalanobis distance. Finally, synthetic positive samples are generated by the chromosome theory of inheritance until the fuzzy representativeness difference of two classes is small. A thorough experimental study on 16 benchmark datasets was performed and the results show that our method is better than other advanced imbalanced classification algorithms in terms of various evaluation metrics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Cordón I, García S, Fernández A, Herrera F (2018) Imbalance: oversampling algorithms for imbalanced classification in r. Knowl-Based Syst 161:329–341

    Google Scholar 

  2. Chawla NV (2009) Data mining for imbalanced datasets: an overview. In: Maimon O (ed). Springer, Boston

  3. Zhou L (2013) Performance of corporate bankruptcy prediction models on imbalanced dataset: the effect of sampling methods. Knowl-Based Syst 41:16–25

    Google Scholar 

  4. Lee Y-H, Hu PJH, Cheng TH, Huang T-C, Chuang W-Y (2013) A preclustering-based ensemble learning technique for acute appendicitis diagnoses. Artif Intell Med 58(2):115–124

    Google Scholar 

  5. Seiffert C, Khoshgoftaar TM, Hulse JV, Folleco A (2014) An empirical study of the classification performance of learners on imbalanced and noisy software quality data. Inf Sci 259:571–595

    Google Scholar 

  6. Ali A, Shamsuddin SM, Ralescu AL (2015) Classification with class imbalance problem: a review[j]. Int J Adv Soft Compu Appl 7(3):176–204

    Google Scholar 

  7. Bo T, He H (2017) Gir-based ensemble sampling approaches for imbalanced learning. Pattern Recogn 71:306–319

    Google Scholar 

  8. Silvia C, Valentina C, Marco V (2014) A method for resampling imbalanced datasets in binary classification tasks for real-world problems. Neurocomputing 135:8

    Google Scholar 

  9. Akkasi A, Varoglu E, Dimililer N (2018) Balanced undersampling: a novel sentence-based undersampling method to improve recognition of named entities in chemical and biomedical text. Appl Intell 48(8):1965–1978

    Google Scholar 

  10. Wang Z, Wang B, Cheng Y, et al. (2019) Cost-sensitive fuzzy multiple kernel learning for imbalanced problem[j]. Neurocomputing 366:178–193

    Google Scholar 

  11. Singh RB, Sanyam S (2018) Class-specific cost-sensitive boosting weighted elm for class imbalance learning[j]. Memetic Computing

  12. Zhu Z, Wang Z, Li D, et al. (2019) Tree-based space partition and merging ensemble learning framework for imbalanced problems[j]. Information Sciences

  13. Lopez-Garcia P, Masegosa AD, Osaba E, Onieva E, Perallos A (2019) Ensemble classification for imbalanced data based on feature space partitioning and hybrid metaheuristics. Appl Intell 49:2807–2822

    Google Scholar 

  14. Chawla NV, Bowyer KW, Hall LO, Philip Kegelmeyer W (2002) Smote: synthetic minority over-sampling technique. J Artif Intell Res 16(1):321–357

    MATH  Google Scholar 

  15. He H, Bai Y, Garcia EA, Li S (2008) Adasyn: adaptive synthetic sampling approach for imbalanced learning. In: Proceedings of the international joint conference on neural networks, IJCNN, part of the IEEE world congress on computational intelligence, WCC, pp 1322–1328

  16. Han H, Wang W, Mao B (2005) Borderline-smote: a new over-sampling method in imbalanced data sets learning. Advances in intelligent computing. In: International conference on intelligent computing ICIC, Part I

  17. Zhang Z (2016) Introduction to machine learning: k-nearest neighbors. Ann Transl Med 4:11

    Google Scholar 

  18. Sutton WS (1903) The chromosomes in heredity. Biol Bull 4(5):231–251

    Google Scholar 

  19. Liu G, Yang Y, Li B (2018) Fuzzy rule-based oversampling technique for imbalanced and incomplete data learning. Knowl-Based Syst 158:154–174

    Google Scholar 

  20. Li L, He H, Liy J, Li W (2018) Edos: entropy difference-based oversampling approach for imbalanced learning. In: 2018 International joint conference on neural NetworksIJCNN

  21. Ho TK (2002) A data complexity analysis of comparative advantages of decision forest constructors. Pattern Anal Appl 5(2):102–112

    MathSciNet  MATH  Google Scholar 

  22. Japkowicz N, Stephen S (2002) The class imbalance problem: a systematic study. Intell Data Anal 6 (5):429–449

    MATH  Google Scholar 

  23. He H, Garcia EA (2009) Learning from imbalanced data. IEEE Trans Knowl Data Eng 21(9):1263–1284

    Google Scholar 

  24. Maciejewski T, Stefanowski J (2011) Local neighbourhood extension of SMOTE for mining imbalanced data. In: Proceedings of the IEEE symposium on computational intelligence and data mining, CIDM 2011, part of the IEEE symposium series on computational intelligence, pp 104–111

  25. Ramentol E, Caballero Y, Bello R, Herrera F (2012) Smote-rsb *: a hybrid preprocessing approach based on oversampling and undersampling for high imbalanced data-sets using smote and rough sets theory. Knowl Inf Syst 33(2):245–265

    Google Scholar 

  26. Bunkhumpornpat C, Sinapiromsaran K, Lursinsap C (2009) Safe-level-smote: safe-level-synthetic minority over-sampling technique for handling the class imbalanced problem. Advances in knowledge discovery and data mining, 13th Pacific-Asia conference, PAKDD proceedings

  27. Barua S, Islam MM, Yao X, Murase K (2014) MWMOTE-majority weighted minority oversampling technique for imbalanced data set learning. IEEE Trans Knowl Data Eng 26(2):405–425

    Google Scholar 

  28. Zhang HX, Li MF (2014) Rwo-sampling: a random walk over-sampling approach to imbalanced data classification. Inf Fusion 20:99–116

    Google Scholar 

  29. Das B, Krishnan NC, Cook DJ (2015) Racog and wracog: two probabilistic oversampling techniques. IEEE Trans Knowl Data Eng 27(1):222–234

    Google Scholar 

  30. Sáez JA, Luengo J, Stefanowski J, Herrera F (2015) SMOTE-IPF: addressing the noisy and borderline examples problem in imbalanced classification by a re-sampling method with filtering. Inf Sci 291(5):184–203

    Google Scholar 

  31. Liu S, Zhang J, Xiang Y, Zhou W (2017) Fuzzy-based information decomposition for incomplete and imbalanced data learning. IEEE Trans Fuzzy Syst 25(6):1476–1490

    Google Scholar 

  32. Liu X-Y, Wu J, Zhou Z-H (2006) Exploratory under-sampling for class-imbalance learning. In: Proceedings of the 6th IEEE international conference on data mining(ICDM 2006), 18-22 December 2006, Hong Kong, China, pp 965–969

  33. Kubat M, Matwin S (1997) Addressing the curse of imbalanced training sets: onesided selection. Proc Int Conf Mach Learn 97:179–186

    Google Scholar 

  34. Jo T, Japkowicz N (2004) Class imbalances versus small disjuncts. SIGKDD Explor 6(1):40–49

    Google Scholar 

  35. Bunkhumpornpat C, Sinapiromsaran K, Lursinsap C (2012) DBSMOTE: density-based synthetic minority over-sampling technique. Appl Intell 36(3):664–684

    Google Scholar 

  36. Yen S-J, Lee Y-S (2009) Cluster-based under-sampling approaches for imbalanced data distributions. Expert Syst Appl 36(3):5718–5728

    Google Scholar 

  37. Lin W-C, Tsai C-F, Hu Y-H, Jhang J-S (2017) Clustering-based undersampling in class-imbalanced data. Inf Sci 409:17– 26

    Google Scholar 

  38. Xindong W, Kumar V, Ross Quinlan J, Ghosh J, Yang Q, Motoda H, McLachlan GJ, Ng AFM, Liu B, Philip SY, Zhou Z-H, Steinbach M, Hand DJ, Steinberg D (2008) Top 10 algorithms in data mining. Knowl Inf Syst 14(1):1–37

    Google Scholar 

  39. Barandela R, Valdovinos RM, Sánchez JS (2003) New applications of ensembles of classifiers. Pattern Anal Appl 6(3):245–256

    MathSciNet  Google Scholar 

  40. Wang S, Yao X (2009) Diversity analysis on imbalanced data sets by using ensemble models. In: Proceedings of the IEEE symposium on computational intelligence and data mining, CIDM, part of the IEEE symposium series on computational intelligence, pp 324–331

  41. Freund Y, Schapire RE (1996) Experiments with a new boosting algorithm, machine learning. In: Proceedings of the thirteenth international conference, pp 148–156

  42. Chawla NV, Lazarevic A, Hall LO, Bowyer KW (2003) Smoteboost: improving prediction of the minority class in boosting. Knowledge discovery in databases: PKDD 2003, 7th European conference on principles and practice of knowledge discovery in databases, pp 107–119

  43. APAZimmermann HJ (2010) Fuzzy set theory. Wiley Interdisciplinary Reviews Computational Statistics 2 (3):317–332

    Google Scholar 

  44. Tang B, He H (2015) ENN: extended nearest neighbor method for pattern recognition [research frontier]. IEEE Comp Int Mag 10(3):52–60

    Google Scholar 

  45. Frey Brendan J, Dueck D (2007) Clustering by passing messages between data points. Science 315 (5814):972–976

    MathSciNet  MATH  Google Scholar 

  46. Bennin KE, Student Member IEEE, Keung J, Member, IEEE, Phannachitta P, Monden A, Member IEEE, Mensah S (2018) MAHAKIL: diversity based oversampling approach to alleviate the class imbalanceissue in software defect prediction. IEEE Trans Softw Eng 44(6):534–550

    Google Scholar 

  47. Zhang X, Song Q, Wang G, Zhang K, He L, Jia X (2015) A dissimilarity-based imbalance data classification algorithm. Appl Intell 42(3):544–565

    Google Scholar 

  48. Mahalanobis PC (1936) On the generalized distance in statistics. Proc Nat Inst Sci (Calcutta) 2:49–55

    MATH  Google Scholar 

  49. Bache K, Lichman M (2013) UCI machine learning repository

  50. Alcalá-Fdez J, Fernández A, Luengo J, Derrac J, García S (2011) Keel data-mining software tool: data set repository integration of algorithms and experimental analysis framework. Multiple-Valued Logic Soft Comput 17(2-3):255–287

    Google Scholar 

  51. Liaw A, Wiener M, et al. (2002) Classification and regression randomforest. R news 2(3):18–22

    Google Scholar 

Download references

Acknowledgements

This research was supported by National Natural Science Foundation of China(61573266).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xidian University, Xi’an, 710126, ShaanXi, China

    Ruonan Ren, Youlong Yang & Liqin Sun

Authors
  1. Ruonan Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Youlong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liqin Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ruonan Ren.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by National Natural Science Foundation of China (61573266).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ren, R., Yang, Y. & Sun, L. Oversampling technique based on fuzzy representativeness difference for classifying imbalanced data. Appl Intell 50, 2465–2487 (2020). https://doi.org/10.1007/s10489-020-01644-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-020-01644-0

Keywords

Search

Navigation