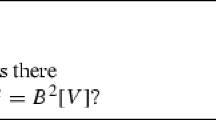Abstract
Given a graph \(G=(V,E)\), an edge bipartization set of G is a subset \(E'\subseteq E(G)\) such that \(G'=(V,E{\setminus } E')\) is bipartite. An edge bipartization set that is also a matching of G is called a bipartizing matching of G. Let \({\mathscr {BM}}\) be the family of all graphs admitting a bipartizing matching. Although every graph has an edge bipartization set, the problem of recognizing graphs G having bipartizing matchings (\(G\in \mathscr {BM}\)) is challenging. A (k, d)-coloring of a graph G is a k-coloring of V(G) such that each vertex of G has at most d neighbors with the same color as itself. Clearly a (k, 0)-coloring is a proper vertex k-coloring of G and, for any \(d>0\), the k-coloring is non-proper, also known as defective. A graph belongs to \(\mathscr {BM}\) if and only if it admits a (2, 1)-coloring. Lovász (1966) proved that for any integer \(k>0\), any graph of maximum degree \(\varDelta \) admits a \(\left( k,\lfloor \varDelta /k \rfloor \right) \)-coloring. In this paper, we show that it is NP-complete to determine whether a 3-colorable planar graph of maximum degree 4 belongs to \(\mathscr {BM}\), i.e., (2, 1)-colorable. Besides, we show that it is NP-complete to determine whether planar graphs of maximum degree 6 or 8 admit a (2, 2) or (2, 3)-coloring, respectively. Due to Lovász (1966), our results are tight in the sense that on graphs with maximum degree three, five, and seven, there always exists a (2, 1), (2, 2), and (2, 3)-coloring, respectively. Finally, we present polynomial-time algorithms for particular graph classes, besides some remarks on the parameterized complexity of the problem of recognizing graphs in \({\mathscr {BM}}\).








Similar content being viewed by others
References
Abdullah, A. (1992). On graph bipartization. In: ISCAS ’92 (Vol. 4, pp. 1847–1850)
Agrawal, A., Jain, P., Kanesh, L., Misra, P., & Saurabh, S. (2019). Exploring the Kernelization Borders for Hitting Cycles. In: 13th international symposium on parameterized and exact computation (IPEC 2018), Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany, Leibniz International Proceedings in Informatics (LIPIcs) (Vol. 115, pp. 14:1–14:14).
Alon, N., & Stav, U. (2009). Hardness of edge-modification problems. Theoretical Computer Science, 410(47–49), 4920–4927.
Andrews, J., & Jacobson, M. (1985). On a generalization of chromatic number. In: Proc. sixteenth southeastern international conference on combinatorics, graph theory and computing (Vol. 47, pp. 18–33).
Angelini, P., Bekos, M. A., De Luca, F., Didimo, W., Kaufmann, M., Kobourov, S., et al. (2017). Vertex-coloring with defects. Journal of Graph Algorithms and Applications, 21(3), 313–340.
Axenovich, M., Ueckerdt, T., & Weiner, P. (2017). Splitting planar graphs of girth 6 into two linear forests with short paths. Journal of Graph Theory, 85(3), 601–618.
Bang-Jensen, J., & Bessy, S. (2019). Degree-constrained 2-partitions of graphs. Theoretical Computer Science. https://doi.org/10.1016/j.tcs.2018.12.023.
Bodlaender, H. L. (1998). A partial \(k\)-arboretum of graphs with bounded treewidth. Theoretical Computer Science, 209(1–2), 1–45.
Bonamy, M., Dabrowski, K. K., Feghali, C., Johnson, M., & Paulusma, D. (2018). Independent feedback vertex set for P\(_5\)-free graphs. Algorithmica. https://doi.org/10.1007/s00453-018-0474-x.
Borodin, O., Kostochka, A., & Yancey, M. (2013). On \(1\)-improper \(2\)-coloring of sparse graphs. Discrete Mathematics, 313(22), 2638–2649.
Brandstädt, A., Dragan, F. F., Le, H. O., & Mosca, R. (2005). New graph classes of bounded clique-width. Theory of Computing Systems, 38(5), 623–645.
Brandstädt, A., Engelfriet, J., Le, H. O., & Lozin, V. V. (2006a). Clique-width for \(4\)-vertex forbidden subgraphs. Theory of Computing Systems, 39(4), 561–590.
Brandstädt, A., Klembt, T., & Mahfud, S. (2006b). \(P_6\)- and triangle-free graphs revisited: structure and bounded clique-width. Discrete Mathematics & Theoretical Computer Science, 8, 173–188.
Burzyn, P., Bonomo, F., & Durán, G. (2006). NP-completeness results for edge modification problems. Discrete Applied Mathematics, 154(13), 1824–1844.
Camby, E., & Schaudt, O. (2016). A new characterization of \(P_k\)-free graphs. Algorithmica, 75(1), 205–217.
Carneiro, A. D. A., Protti, F., & Souza, U. S. (2019). Deadlock resolution in wait-for graphs by vertex/arc deletion. Journal of Combinatorial Optimization, 37(2), 546–562. https://doi.org/10.1007/s10878-018-0279-5.
Choi, H. A., Nakajima, K., & Rim, C. S. (1989). Graph bipartization and via minimization. SIAM Journal on Discrete Mathematics, 2(1), 38–47.
Chuangpishit, H., Lafond, M., & Narayanan, L. (2018). Editing graphs to satisfy diversity requirements. In D. Kim, R. N. Uma & A. Zelikovsky (Eds.), Combinatorial Optimization and Applications (COCOA 2018) (pp. 154–168). Cham: Springer.
Courcelle, B. (1990). The monadic second-order logic of graphs. I. Recognizable sets of finite graphs. Information & Computation, 85(1), 12–75.
Courcelle, B. (1997). Handbook of graph grammars and computing by graph transformation. In G. Rozenberg (Ed.), The expression of graph properties and graph transformations in monadic second-order logic (pp. 313–400). River Edge: World Scientific Publishing Co., Inc.
Courcelle, B., & Engelfriet, J. (2012). Graph structure and monadic second-order logic: a language-theoretic approach. New York: Cambridge University Press.
Courcelle, B., & Mosbah, M. (1993). Monadic second-order evaluations on tree-decomposable graphs. Theoretical Computer Science, 109(1–2), 49–82.
Courcelle, B., Makowsky, J. A., & Rotics, U. (2000). Linear time solvable optimization problems on graphs of bounded clique-width. Theory of Computing Systems, 33(2), 125–150.
Cowen, L., Cowen, R., & Woodall, D. (1986). Defective colorings of graphs in surfaces: partitions into subgraphs of bounded valency. Journal of Graph Theory, 10, 187–195.
Cowen, L., Goddard, W., & Jesurum, C. E. (1997). Defective coloring revisited. Journal of Graph Theory, 24(3), 205–219.
Cygan, M., Fomin, F. V., Kowalik, L., Lokshtanov, D., Marx, D., Pilipczuk, M., et al. (2015). Parameterized algorithms. Berlin: Springer.
Diestel, R. (2010). Graph theory (4th ed., Vol. 173). Berlin: Springer.
Dorbec, P., Montassier, M., & Ochem, P. (2014). Vertex partitions of graphs into cographs and stars. Journal of Graph Theory, 75(1), 75–90. https://doi.org/10.1002/jgt.21724.
Downey, R. G., & Fellows, M. R. (2013). Fundamentals of parameterized complexity. Texts in computer science. Berlin: Springer.
Eaton, N., & Hull, T. (1999). Defective list colorings of planar graphs. Bulletin of the Institute of Combinatorics and its Applications, 25, 79–87.
Furmańczyk, H., Kubale, M., & Radziszowski, S. (2016). On bipartization of cubic graphs by removal of an independent set. Discrete Applied Mathematics, 209, 115–121.
García-Vázquez, P. (2016). On the bipartite vertex frustration of graphs. Electronic Notes in Discrete Mathematics, 54, 289–294. https://doi.org/10.1016/j.endm.2016.09.050.
Garey, M., Johnson, D., & Stockmeyer, L. (1976). Some simplified NP-complete graph problems. Theoretical Computer Science, 1(3), 237–267.
Gimbel, J., & Nešetřil, J. (2010). Partitions of graphs into cographs. Discrete Mathematics, 310(24), 3437–3445. https://doi.org/10.1016/j.disc.2010.07.011.
Golumbic, M. C., & Rotics, U. (2000). On the clique-width of some perfect graph classes. International Journal of Foundations of Computer Science, 11(03), 423–443.
Guillemot, S., Havet, F., Paul, C., & Perez, A. (2012). On the (non-)existence of polynomial kernels for \(p\)-free edge modification problems. Algorithmica, 65(4), 900–926.
Harary, F., & Jones, K. (1985). Conditional colorability ii: Bipartite variations. In: Proc. sundance cont. combinatorics and related topics, congr. numer. (Vol. 50, pp. 205–2018)
Hopcroft, J., & Tarjan, R. (1974). Efficient planarity testing. Journal of the ACM, 21(4), 549–568.
Lampis, M. (2012). Algorithmic meta-theorems for restrictions of treewidth. Algorithmica, 64(1), 19–37.
Lima, C. V., Rautenbach, D., Souza, U. S., & Szwarcfiter, J. L. (2017). Decycling with a matching. Information Processing Letters, 124, 26–29.
Lovász, L. (1966). On decomposition of graphs. Studia Scientiarum Mathematicarum Hungarica, 1, 237–238.
Mulzer, W., & Rote, G. (2008). Minimum-weight triangulation is NP-hard. Journal of the ACM, 55(2), 1–29.
Natanzon, A., Shamir, R., & Sharan, R. (2001). Complexity classification of some edge modification problems. Discrete Applied Mathematics, 113(1), 109–128.
Protti, F., & Souza, U. S. (2018). Decycling a graph by the removal of a matching: New algorithmic and structural aspects in some classes of graphs. Discrete Mathematics & Theoretical Computer Science. https://doi.org/10.23638/DMTCS-20-2-15.
Robertson, N., & Seymour, P. (1986). Graph minors ii algorithmic aspects of tree-width. Journal of Algorithms, 7(3), 309–322.
Schaefer, TJ. (1978). The complexity of satisfiability problems. In: STOC ’78 (pp. 216–226)
Thorup, M. (1998). All structured programs have small tree width and good register allocation. Information and Computation, 142(2), 159–181.
Yannakakis, M. (1978). Node-and edge-deletion NP-complete problems. In: STOC ’78 (pp. 253–264)
Yannakakis, M. (1981). Edge-deletion problems. SIAM Journal on Computing, 10(2), 297–309.
Yarahmadi, Z., & Ashrafi, A. R. (2014). A fast algorithm for computing bipartite edge frustration number of \((3,6)\)-fullerenes. Journal of Theoretical and Computational Chemistry, 13(02), 1450014–1–1450014–11.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) Finance Code 001, by the Conselho Nacional de Desenvolvimento Científico e Tecnológico - Brasil (CNPq) - Grant Numbers: (CNPq/DAAD2015SWE/290021/2015-4, 303726/2017-2, 309832/2020-9), and FAPERJ (Grant Number: E-26/203.272/2017). A conference version appeared in the Proc. of the 12th Annual International Conference on Combinatorial Optimization and Applications (COCOA), Volume 11346, pages 198–213, Atlanta, USA, December 2018.
Rights and permissions
About this article
Cite this article
Lima, C.V.G.C., Rautenbach, D., Souza, U.S. et al. On the computational complexity of the bipartizing matching problem. Ann Oper Res 316, 1235–1256 (2022). https://doi.org/10.1007/s10479-021-03966-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-03966-9
Keywords
- Graph modification problems
- Edge bipartization
- Defective coloring
- Planar graphs
- NP-completeness
- Parameterized complexity